Content
Acoustic Plane Wave Properties
Acoustic Pressure
Acoustic Pressure Addition
Acoustic Plane Wave Properties
The acoustic pressure caused by an acoustic disturbance varies with both time and position. Besides studying of the fluctuation of acoustic pressure that associated with a sound wave with respective to time at any point, many practical problems focus on the pressure variation caused by the sound at any point with respective to position.
Acoustic Pressure
The acoustic pressure at any point varies with time sinusoidally, the root mean square is more convenient to be used to measure the alternating pressure fluctuation by taking the square root of the average of squares of instantaneous acoustic pressures within a period T. That is
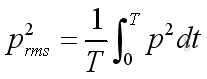
where
prms is the root mean square of acoustic pressures
T is the period of measurement
p is the instantaneous acoustic pressures
The instantaneous acoustic pressure can be expressed as:
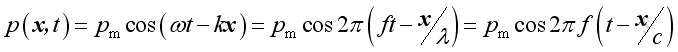
where
p(x,t) is the instantaneous acoustic pressures
x is distance
t is time
pm is the maximum of the instantaneous acoustic pressures
ω is angular velocity
k is wave number
ƒ is frequency
λ is wave length
Therefore:
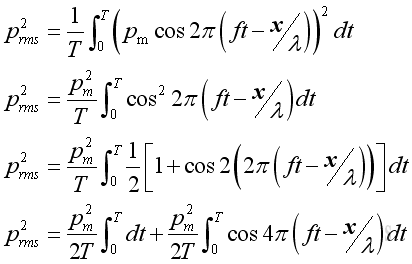
Since the time average of a cosine function of function of time equals to zero, imply :
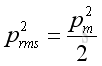 or
or
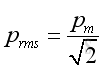
Acoustic Pressure Addition
The addition of two sound pressures of different frequency equals to:
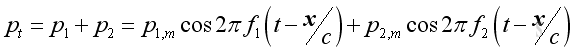
Imply the square of the total sound pressure is
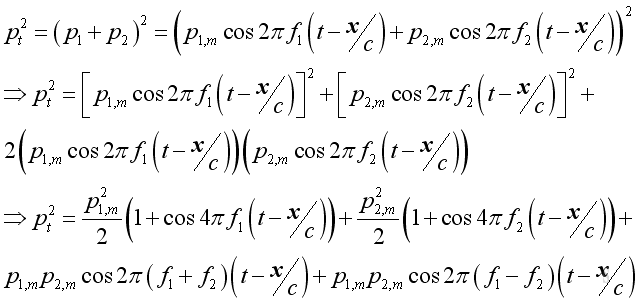
The root mean square value of the total the total acoustic pressure can be obtained by taking the time average process. Similarly, the cosine term of function of time equal s to zero, and get
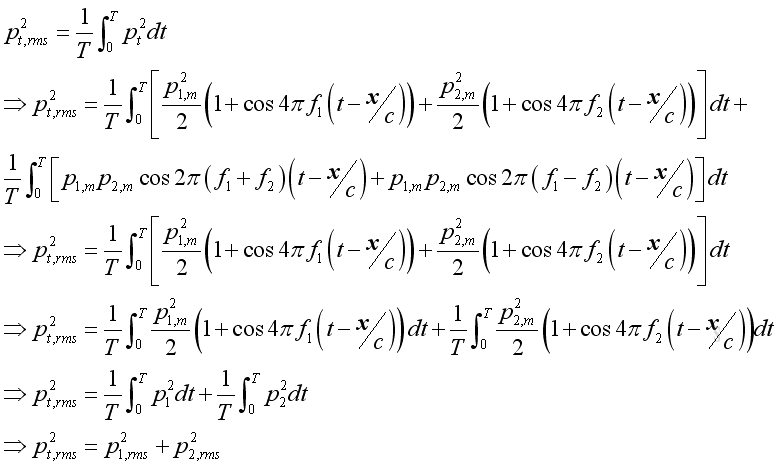
Therefore. the total acoustic pressure of the two equal sound pressure due to two noises of different frequencies are only the √2 times of the sound pressure due to either noise source. The result can also be extended to a continuous bands of frequencies. However, when the two frequencies are equal and coherent, the result will be different.
When there is the present of phase angle, the result becomes
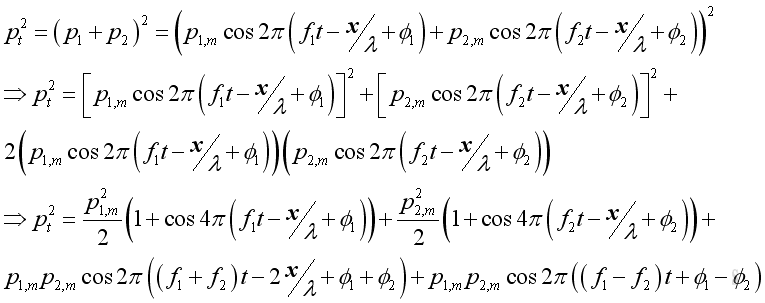
Since the time average of the cosine terms of functions of time is zero, the phase angle does not affect the result of sounds with different frequencies. However, the phase angle affects the result when the frequencies of two sound sources are the same. By taking the time average, the equation with same frequency becomes:
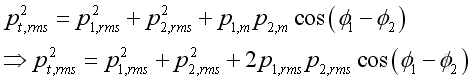
Acoustic Intensity
Acoustic intensity is the sound power passing through a unit area, it can be considered as the rate of transmitting energy through the medium cross section area by medium fluctuation due to sound wave. The vibration of medium composes the change in both potential and kinetic energy.
Assuming constant mass and at initial state both potential energy and kinetic energy are zero with the acoustic disturbance equals zero. The potential energy EPE and kinetic energy EKE of an infinitesimal element of volume Vo due to acoustic fluctuation along x direction is:
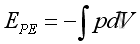 ,
,
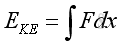
From the linearized continuity equation, where s is the acoustic displacement,
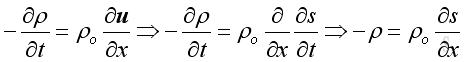
Substitute the speed of propagation,
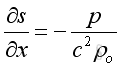
The volume of the infinitesimal element can be expressed as,
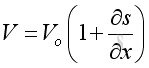
Substitute the differential in term of pressure, then
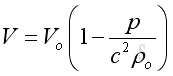
The differential volume can then be equals to:
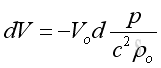
Therefore the potential energy is:
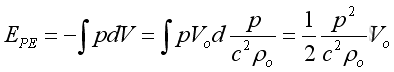
For the kinetic energy, substitute the velocity in term of pressure :
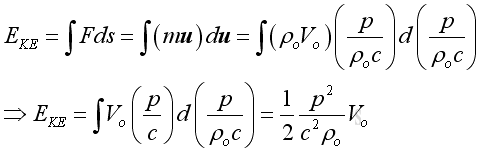
Therefore the total instantaneous energy of an infinitesimal element due to acoustic disturbance is:
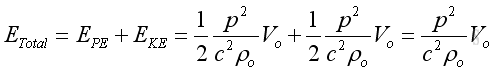
Since the wave propagate at the speed of s, the volume of infinitesimal element per unit area in time δt can be expressed as:
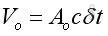
As the instantaneous intensity is the rate of energy flow through a unit area, imply:
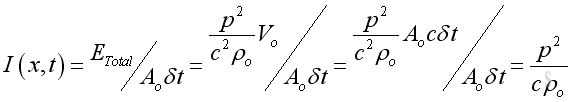
Or, in term of acoustic pressure and acoustic velocity:
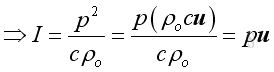
Similar to the pressure, the intensity usually expressed as an average in practice, imply:
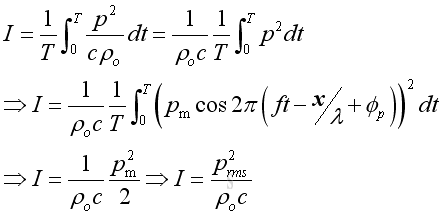
In form of complex exponential representation, the intensity equals to the real active component of intensity:
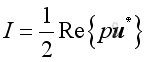
Imply
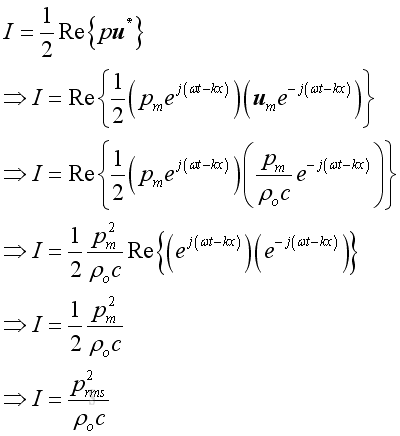
Acoustic Power of Plane Wave
Sound power is defined as the integration of intensity over the surface area enclosing the enclosure and is
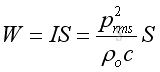
SPL and SIL of Plane Wave
The Sound Pressure Level of a plane wave:
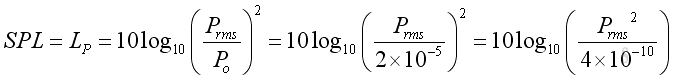
Assume ρo = 1.2kg/m3, c = 334m/s,the Sound Intensity Level of a plane wave:
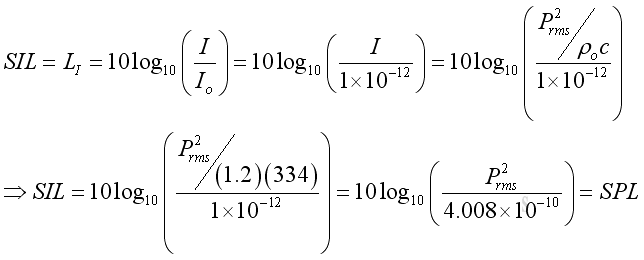
Plane Wave Example
A plane wave propagates with a frequency of 50Hz and maximum pressure amplitude 150Pa in positive x direction with characteristic that at time t = 0 and at x = 0, the plane wave in term of acoustic pressure can be expressed as:
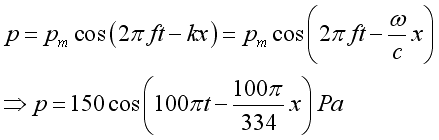
The corresponding plane wave in term of medium velocity can be expressed as:
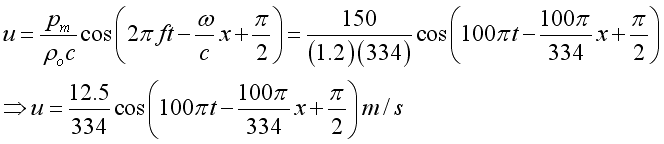
The mean intensity of the plane wave can be expressed as:
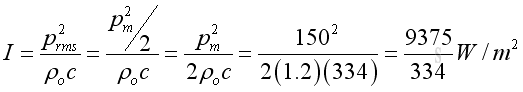
The sound intensity level of the plane wave in term of dB can be expressed as:
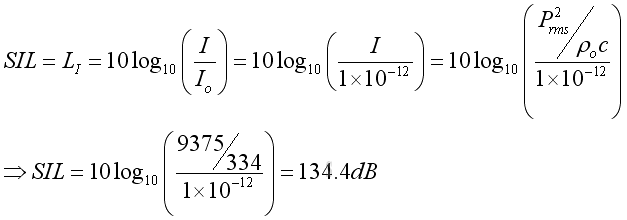
©sideway
ID: 100900023 Last Updated: 10/9/2010 Revision: 1 Ref:
References
- Michael P. Norton; Denis G. Karczub,, 2003, Fundamentals of Noise and Vibration Analysis for Engieer
- G. Porges, 1977, Applied Acoustics
- Douglas D. Reynolds, 1981, Engineering Principles of Acoustics:; Noise and Vibration Control
- Conrad J. Hemond, 1983, Engineering Acoustics & Noise Control
- F. Fahy, 2001, Foundations of Engineering Acoustics
- D.A. Biew; C.H. Hansen, 1996, Engineering Noise Control: Theory and Practice
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
