Content

Acoustic Spherical Wave

When a small spherical sound source propagates outward uniformly and radically in a free space. The acoustic functions are spherically symmetric and therefore are functions of time and radial coordinate only.

Acoustic Spherical Wave Equation

Since there is no tangential motion during wave propagation, the spatial operator on the pressure in the wave equation can be converted to

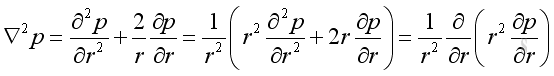
substitute the spherical operator into the rectangular wave equation:

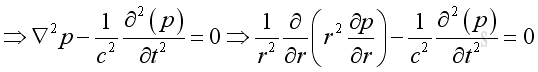
Therefore the 3D wave equation in spherical coordinate system is:

 

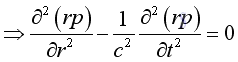
Acoustic Spherical Wave

The general solution of the spherical wave is:

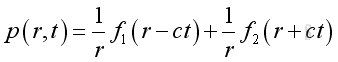
for harmonic wave, it can be expressed as

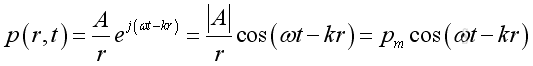
or

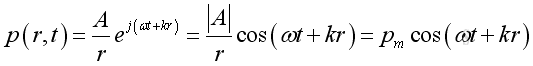
The acoustic pressure of a spherical wave is inversely proportional to the distance from the source. Therefore when the distance r is doubled, the pressure will be reduced by 6dB.

Since there is no tangential motion in spherically symmetric wave, a linearized relationship with spherical coordinates between radial velocity and radial pressure from the momentum conservation can be obtained:

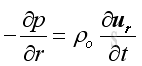
Assume the radial velocity of the form

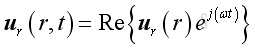
The time derivative of the velocity is:

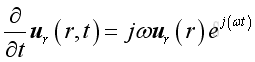
Substitute all variables into the momentum conservation equation and get the radial velocity in term of its acoustic pressure :

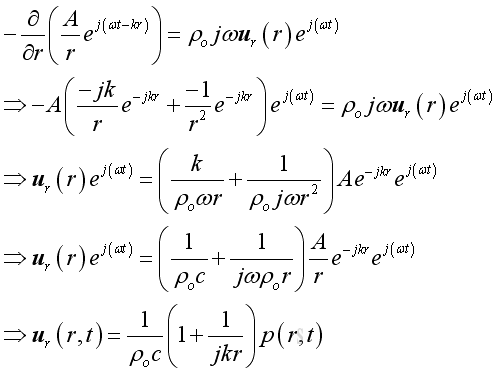
Substitute acoustic pressure into the acoustic velocity imply the real part of acoustic velocity :

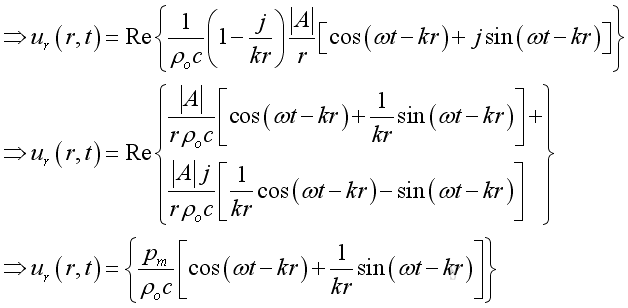
Therefore the modulus or absolute value is:

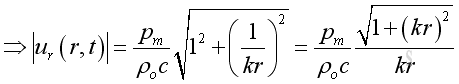
The acoustic velocity composes of two parts.  The first part is in phase with the acoustic pressure with property 1/r as the propagating part. While the second part is not in phase with the acoustic pressure with property 1/r² as the evanescent part. When the in phase component is comparable to the not in phase component, the position of interest is in the near field. Otherwise it is in the far field.

The root mean square velocity is:

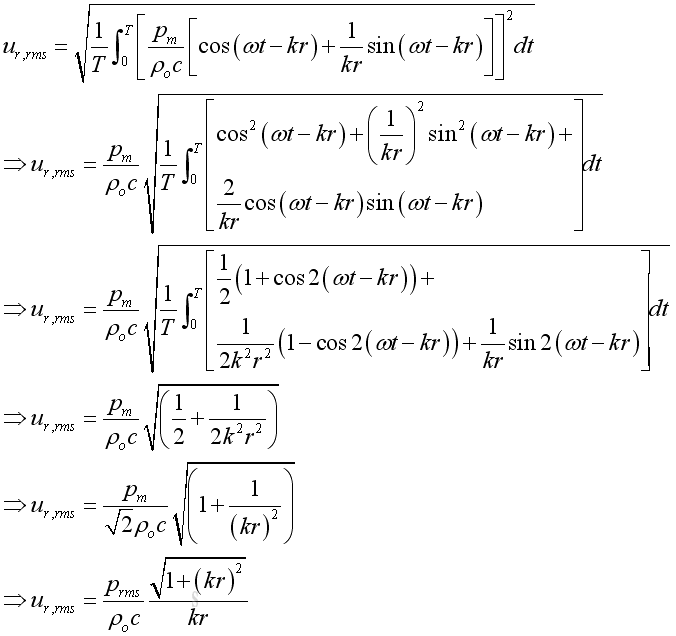
Acoustic Intensity

Similar to the plane wave, the instantaneous intensity is:

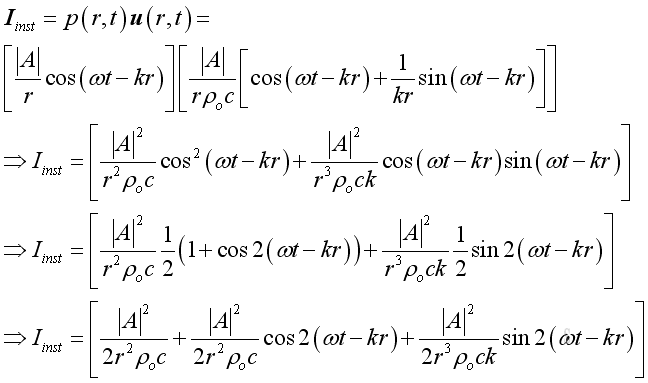
Similarly, the intensity usually expressed as an average in practice. The mean or time average intensity, in which the cosine and sine term of  function of time becomes zero, imply:

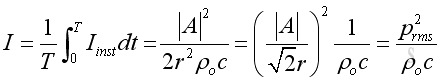
Although the expression for a spherical wave is same as that for the plane wave, the root mean square acoustic pressure is no longer a constant and is inversely proportion to the distance r from the source.

Besides, only the propagating component contributes the intensity. The evanescent component is not in phase with the pressure becomes zero after the time average process because of its oscillating property

Acoustic Power

The total acoustic power is the integration of intensity over the spherical area enclosing the enclosure and equals

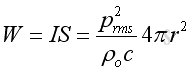
The total acoustic power is a constant and independent of distance r. Since the acoustic pressure is inversely proportion to r and the spherical surface area is proportion to r². As intensity is proportion to square acoustic pressure, the distance r will be cancelled.