Content
Body Force of 2D
Plane Body
Center of Gravity of a Plane Plate
Center of Gravity of a Plane Wire
Center of Mass
Centroid of Area
Centroid of Line
Body Force of 2D Plane Body

When the thickness of a three dimensional body is small and uniform, the body can be condsidered as a plane body. The weight of the body is equal to the force exerted by the earth on the body.
Center of Gravity of a Plane Plate
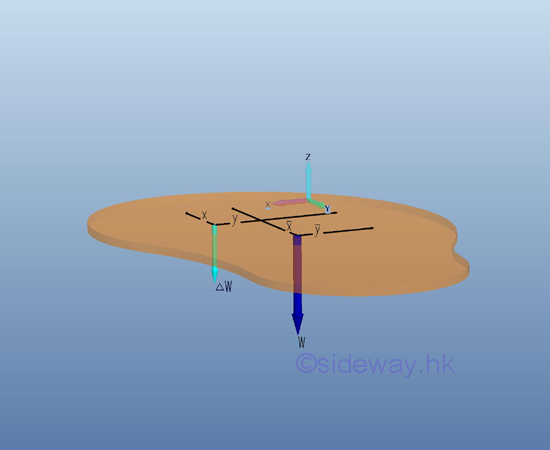
The force of gravity acts on each of the particles of the entire body. By dividing the plate into small finite regions or elements, the weight of the body can also be divided into small forces distributing over the plane plate. For a plane plate of n element, the weight of the plane plate is equal to
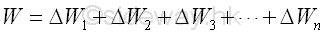
As in the equivalent systems of forces, two systems of forces are equivalent at the point of interest, if:
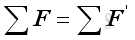 and
and
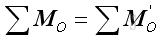
By assuming the forces exerted by the earth on the elements of plane plate are parallel, the resultant force is equal to a single force in the same direction. Therefore, the magnitude of the body force of the plane plate is
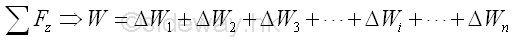
By denoting the position of the element of the plane plate relative to the coordinate system as xi,yi, the coordinates x , y of the center of gravity of the plane plate where the resultant force W applied can be determined by equating the moment of the resultant force W about the y and x axes and the corresponding mements of elements of the plane plate about the coordinate axis respectively. Imply
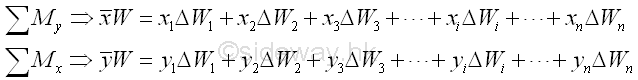
Therefore the coordinates x , y of the center of gravity of the plane plate is
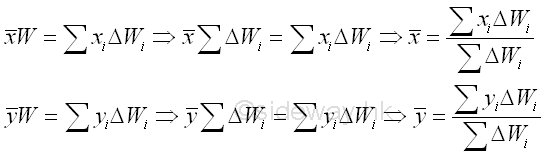
When the number of elements n is increaed toward infinity by taking the limit as the size of each element approaches zero, the magnitude of weight and the position of center of gravity of the plane plate can be determined by,
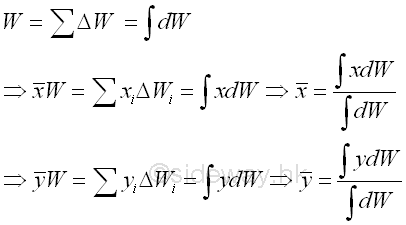
Center of Gravity of a Plane Wire
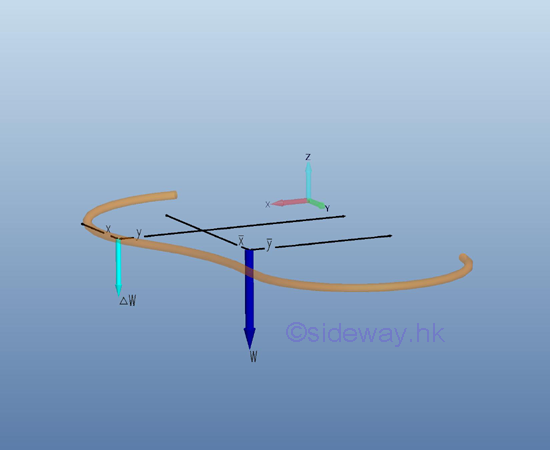
When the plane body is in the form of plane wire lying in the xy plane, the magnitude of weight and the position of center of gravity of the plane plate can be determined in the similar way. The derived equation is same as the plane plate, imply
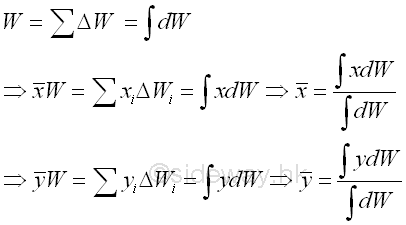
Although the center of gravity of a plate is usually located on the plate, the center of gravity of a wire is usually not located on the wire.
Center of Mass
The weight of an object is the gravitational force exerted by the earth on the body and can be defined as the mass of the object times the acceleration due to gravity between the object and the earth. Mass is the fundamental property of an object and is defined as the numerical measure of the amount of inertia matter of the object. Although, in general, the gravitational force field of earth is not uniform. For example, the gravitational force on an artificial satellite is not uniform. But for practical static mechanical problems, the gravitational force of earth acting on an object is usually assumed to be uniform at all places. For an uniform gravitational force field,
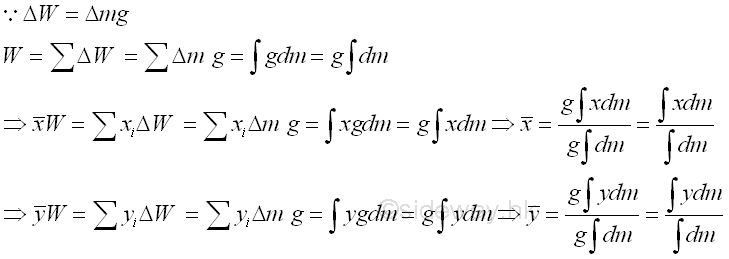
Therefore, the center of mass is same as the center of gravity in an uniform gravitational force field.
Centroid of Area
The weight of an object can also be expressed in terms of density, ρ. For a homogenous two dimensional body, plate of uniform thickness, t, the weight of an element of the plane body of area, ΔA can be expressed as,
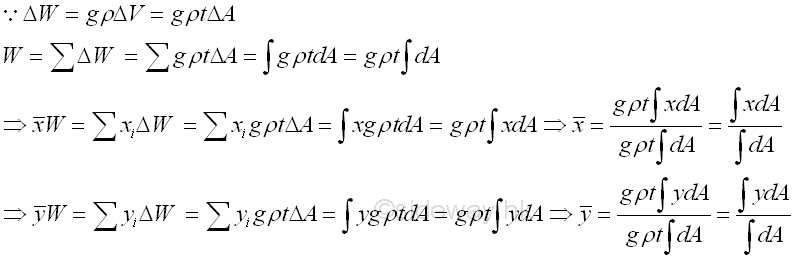
Therefore, the centroid of area of a homogeneous two dimensional body, plate of uniform thickness in an uniform gravitational force field is same as the center of gravity or center of mass.
Centroid of Line
Similarly, for a homogenous two dimensional body, wire of uniform cross-section, a, the weight of an element of the wire of length, ΔL can be expressed as,
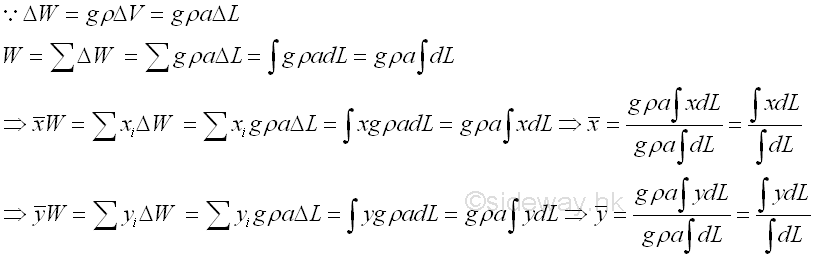
Therefore, the centroid of line of a homogeneous two dimensional body, wire of uniform cross-section in an uniform gravitational force field is same as the center of gravity or center of mass.
©sideway
ID: 120400002 Last Updated: 4/4/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
