Content
Theorems of Pappus-Guldinus
Theorem 1: Surface of Revolution
Surface of Revolution
Theorem 2: Body of Revolution
Body of Revolution
Applications of
Theorems of Pappus-Guldinus
Surface of Revolution
Solid of Revolution
Theorems of Pappus-Guldinus
The theorems of Pappus-Guldinus were formulated by the Greek geometer Pappus of Alexandria during the 4th century A.D. (about 340 A.D.) and were restated by the Swiss mathematician Paul Guldinus (1640). The two theorems of Pappus-Guldinus describe the area of surface of revolution and the volume of body of revolution by the circular path traversed by their centroid during the revolution.
Theorem 1: Surface of Revolution
For the surface of a surface of revolution generated by the rotation of a plane curve about a non-intersecting axis, the surface area A of the surface of revolution is equal to the product of the curve length L of the generating curve and the travelled distance d of the centroid of the generating curve during the generation of the surface by revolution. And the travelled distance of the centroid by revolution can also be expressed in terms of the perpendicular distance y of the centroid away from the rotating axis.
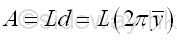
Surface of Revolution
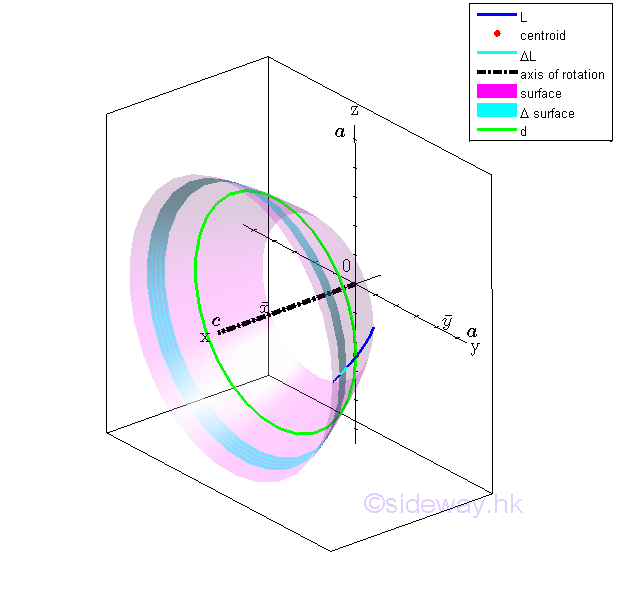
The area A of the surface of revolution can be determined by integration through the revolution of an elemental segment dL. Imply
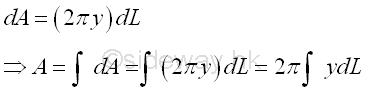
The area A can be rearranged in the form of the integral of the first moment of an elemental segment , which can also be expressed in terms of the centrod of the generating curve, Imply
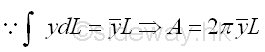
Theorem 2: Body of Revolution
For the body of a body of revolution generated by the rotation of a plane region about a non-intersecting axis, the body volume V of the body of revolution is equal to the product of the area A of the generating plane region and the travelled distance d of the centroid of the generating region during the generation of the body by revolution. And the travelled distance of the centroid by revolution can also be expressed in terms of the perpendicular distance y of the centroid away from the rotating axis.
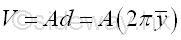
Body of Revolution
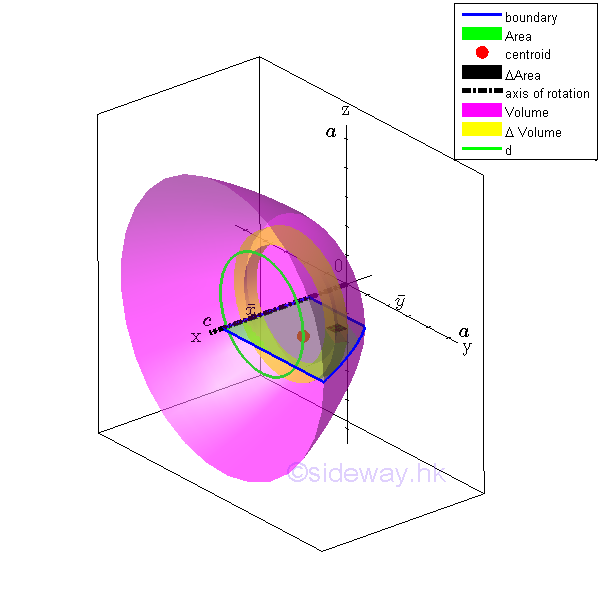
The volume V of the body of revolution can be determined by integration through the revolution of an elemental area dA. Imply
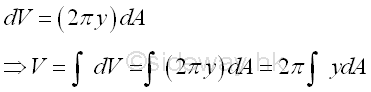
The volume V can be rearranged in the form of the integral of the first moment of an elemental area, which can also be expressed in terms of the centrod of the generating area, Imply
Applications of Theorems of Pappus-Guldinus
The Theorems of Pappus-Guldinus provides a simple relationship between the area of surface of revolution or the volume of body of revolution and the centroid of the generating plane curve or the centroid of the generating plane area. Therefore the Theorems of Pappus-Guldinus can be used to determine the area of surface of revolution and the volume of body of revolution from the generating curve and the generating area accordingly. And the centroid of a generating plane curve and the centroid of a generating plane area can also be determined from the surface of revolution and body of revolution accordingly.
Surface of Revolution
Cylinder

Area of cylinder of surface of revolution is
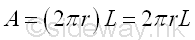
Area of cylinder of surface of revolution by theorem of Pappus-Guldinus is
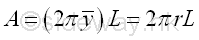
Cone

Area of cone of surface of revolution is
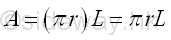
Area of cone of surface of revolution by theorem of Pappus-Guldinus is
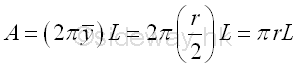
Sphere
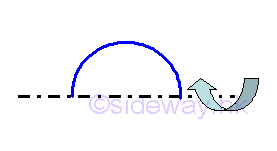
Area of sphere of surface of revolution is
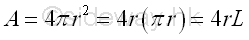
Area of sphere of surface of revolution by theorem of Pappus-Guldinus is
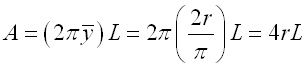
Torus

Area of torus of surface of revolution is
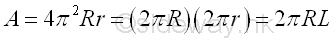
Area of torus of surface of revolution by theorem of Pappus-Guldinus is
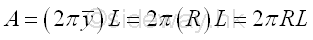
Solid of Revolution
Cylinder
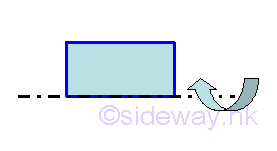
Volume of cylinder of body of revolution is
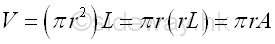
Volume of cylinder of body of revolution by theorem of Pappus-Guldinus is
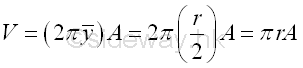
Cone

Volume of cone of surface of revolution is
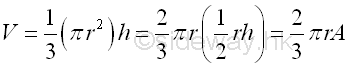
Volume of cone of surface of revolution by theorem of Pappus-Guldinus is
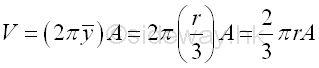
Sphere
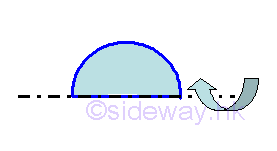
Volume of sphere of surface of revolution is
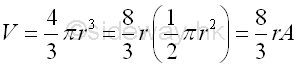
Volume of sphere of surface of revolution by theorem of Pappus-Guldinus is
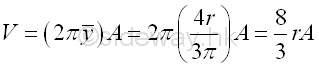
Torus
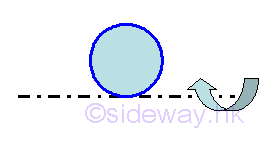
Volume of torus of surface of revolution is
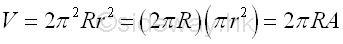
Volume of torus of surface of revolution by theorem of Pappus-Guldinus is
©sideway
ID: 120700003 Last Updated: 7/9/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
