Content
Applications of
Friction Forces
Journal Bearings
Journal Bearing with Parallel
Forces Example 1
Journal Bearing with Parallel
Forces Example 2
Journal Bearing with
Non-Parallel Forces Example
Applications of Friction Forces
Frictional forces are also found in many common practical tools and machines with rotating members.
Journal Bearings
There are lateral supports for every rotating members in tools and machines. Journal bearings are usually used for providing lateral support to rotating shafts and axles. If there is no lubrication between the rotating axle and the bearing, the axle friction is the dry friction between two contact surfaces only. For example, a wheel of 2W is rigidly mounted on an axle which is supported by two jounal bearings mounted symmetrically on both sides. As a result, the loading acting on one journal bearing is equal to W.

Because of the presence of friction forces between contact surfaces of the axle and the bearings, a couple of 2M is needed to maintain the wheel rotating at constant speed. Therefore the forces through the centre O exerted on the journal bearing at one end is the weight W and the couple M. And the reaction forces supplied by the journal bearing at centre O is the reaction force R of magnitude equal to W and a couple M due to dry friction of the same magnitude but opposite in sense.
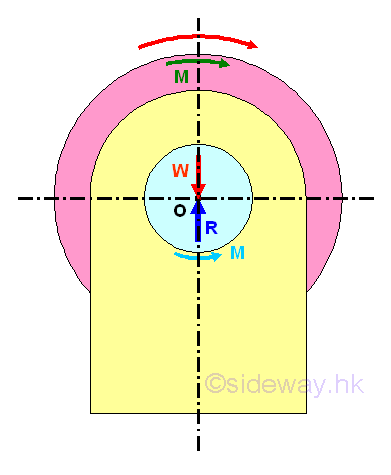
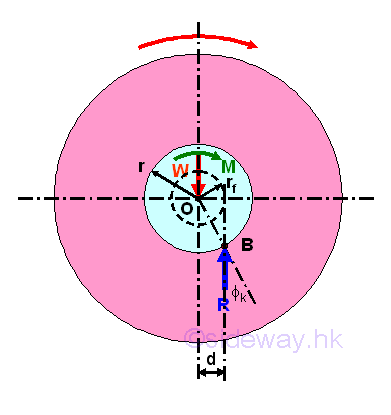
In other words, for the forces analysis of axle and journal bearing, an additional couple M is needed to overcome the frictional force under motion in static equilibrium. When the axle and journal bearing are in stationary contact, the couple M equal to zero and therefore the reaction force R should pass through centre O and the point of application at which the point of contact applied is at the lowest point A. But when the axle rotates at constant velocity or is under motion in static equilibrium, the presence of an additional couple M causes the point of contact of axle to shift away from the lowest point. The point of application B can be determined by transforming the system of reaction forces to a single reaction force vector and a perpendicular distance from the point of interest, centre O. Therefore, the axle will climbs up in the journal bearings to the point of application where slippage occurs.
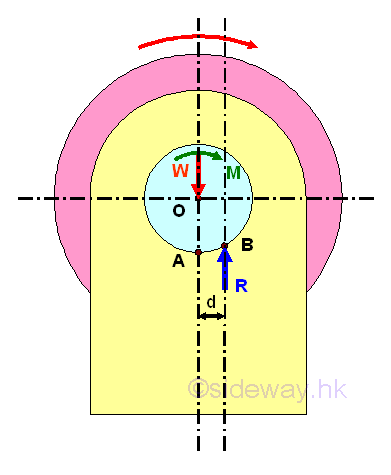
And the couple M is equal to the reaction moment due to the friction force. Since the friction force is a tangential reaction force along the circular contact surfaces, the profile of contact surface axle and the bearing can be simplified by assuming the contract surfaces are in a single symmetric straght line at the point of direct contact. Because of the kinetic friction, the position of the point of application is therefore can be determined by the angle between the reaction R and the normal to the contact surface and the angle is equal to the angle of kinetic friction Φk. Imply
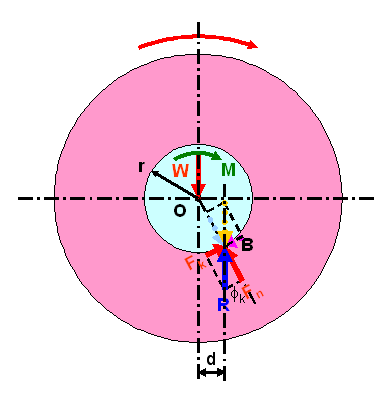
The distance d of the point of application can be determined by the equilibrium equation. Imply
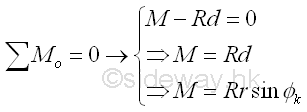
For bearing with small friction coefficient, the angle of friction is a small value also, therefore sin Φk can be approximated by tan Φk which is equal to μk. Imply
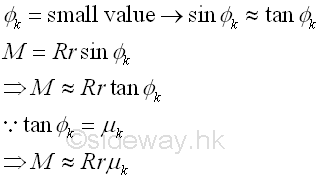
Since the applied load W on an axle is not alway pointing downward, the line of action of reaction force R can be expressed as the tangent line to a circle of radius rf centred at O. Imply.
And the circle is called the circle of friction of the axle and bearing. Since the radius of the circle of friction is the perpendicular distance of the moment due the friction force only, the loading conditions of the axle doest not affect the radius of the circle. And the radius of the circle is
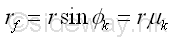
Journal Bearing with Parallel Forces Example 1
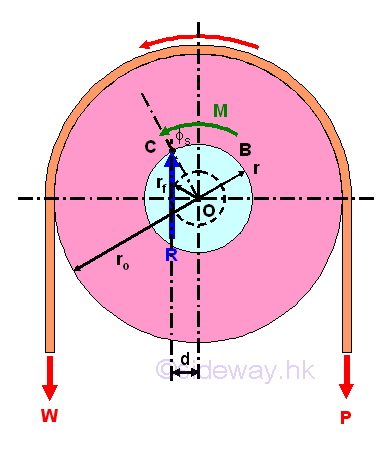
For example, a pulley with journal bearing is used to just about to start lifting up a load W by applying a smallest downward force P.
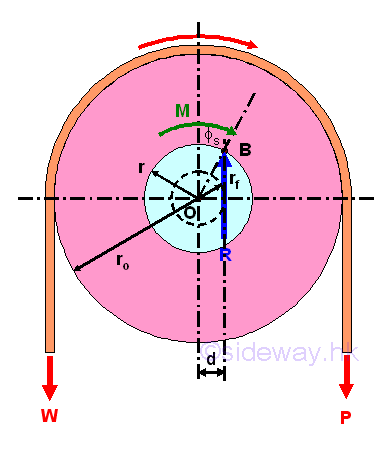
In order to overcome the frictional force between the axle and bearing, the applied force P used to lift up the load W is greater than the load W. And therefore the contact point of the axle and bearing will shift to the right at point B. Since the load W is just about to start moving, the angle of friction used is angle of static friction is used instead of angle of kinetic friction. The perpendicular distance d of the line of action of the reaction force R away from the center O is
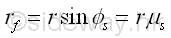
Therefore the smallest applied force P for the impending motion can be determined by equilibrium equations. Consider moment about O, imply
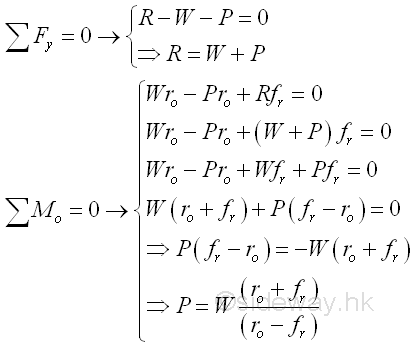
Journal Bearing with Parallel Forces Example 2
For example, a pulley with journal bearing is used to just about to start lowering down a load W by applying a smallest downward force P.
Before the load W can be lowered, the load W should overcome the frictional force between the axle and bearing, the applied force P used to hold the load W with downward impending motion is less than the load W. And therefore the contact point of the axle and bearing will shift to the left at point C. Since the load W is just about to start moving, the angle of friction used is angle of static friction is used instead of angle of kinetic friction. The perpendicular distance d of the line of action of the reaction force R away from the center O is
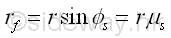
Therefore the smallest applied force P for the impending motion can be determined by equilibrium equations. Consider moment about C, imply
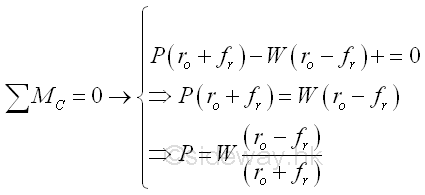
Journal Bearing with Non-Parallel Forces Example
For example, a pulley with journal bearing is used to just about to start lifting up a load W vertically by applying a smallest horizontal force P.
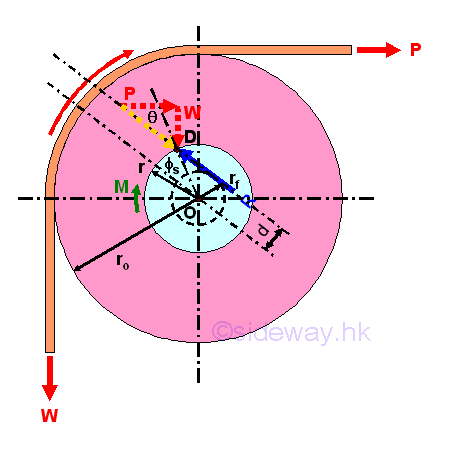
In order to overcome the frictional force between the axle and bearing, the applied force P used to lift up the load W is greater than the load W. And therefore the contact point of the axle and bearing will shift to the applied force P side at point D. Since the load W is just about to start moving, the angle of friction used is angle of static friction is used instead of angle of kinetic friction. The perpendicular distance d of the line of action of the reaction force R away from the center O is
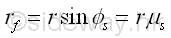
Let the angle between the resultant force R and the Applied force P be θ. The relationships of the smallest applied force P for the impending motion, the load W and the resultant force R can be determined by equilibrium equations. Consider moment about point C, imply
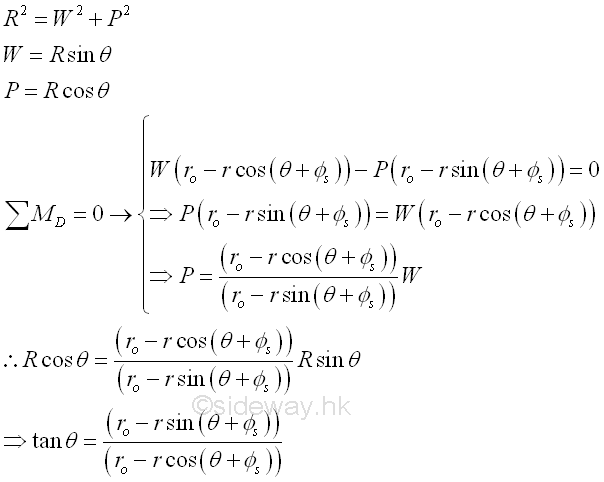
The relationships of the smallest applied force P for the impending motion, the load W and the resultant force R can also be determined by equilibrium equations with the consideration of moment about centro O, imply
Graphically,
And the angle θ by sine rule,
And the smallest applied force P for the impending motion can be obtained by
Besides, since the three force W, P, and R are not parallel, the relationships of the smallest applied force P for the impending motion, the load W and the resultant force R can also be determined by assuming they are concurrent at point E. Imply
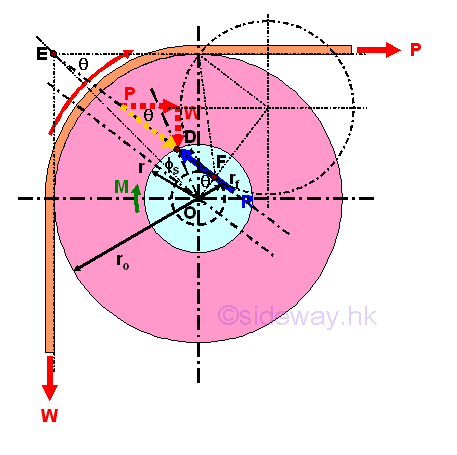
Since the three forces are concurrent. the lines of action of all three forces, i.e. W, P, and R, must pass through the point E. And because of the reactive friction force, the resultant force R must tangent to the circle of friction also. Therefore the reactive friction force can be expressed as an rotating angle of the resultant force R at point E. The angle of rotation is
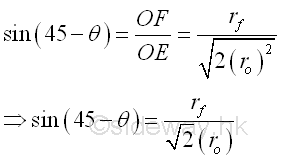
And the smallest applied force P for the impending motion can be obtained by
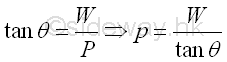
©sideway
ID: 120800010 Last Updated: 8/12/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
