Content
Work and Energy
Work of a Force
Conservative Force
Non-Conservative Force
Work of Conservative Weight
Work of Conservative Spring Force
Potential Energy
Equilibrium
Example of Potential Energy in Equilibrium
Stability of Equilibrium
Work and Energy
The work by applying a force on a body for an infinitesimal displacement can be referred as the kinetic work done by the applied force for a stationary rigid body to change its position because the displacement of the rigid body can be related to the kinetic energy of the rigid body under consideration. But for a conservative system, since the work done on a body is indendent of the travelled path and is completely reversible, the work done by a conservative force can also be refered as the change of its potential energy according to the change of its position.
Work of a Force
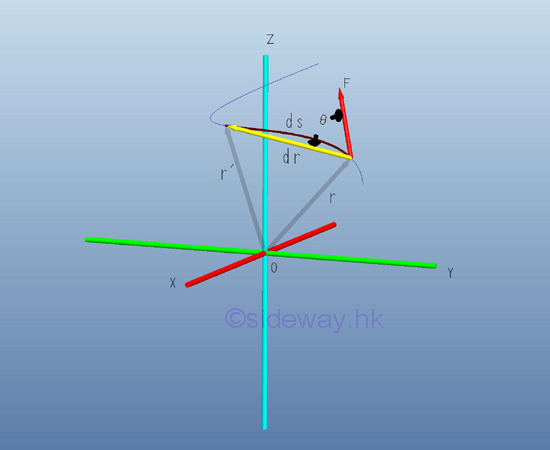
Since an infinitesimal work done by a force acting on a particle with an differential displacement can be expressed as the scalar product of the force vector and the differential displacement vector. The work of a force acting on a particle along a curve can be obtained by integration over the path C travelled by the particle. Imply
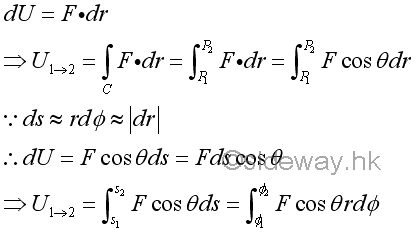
Graphically, the definite integral of work along the travelled path can be represented by the area under the curve of the graph of Fcosθ again s in an xy plane.
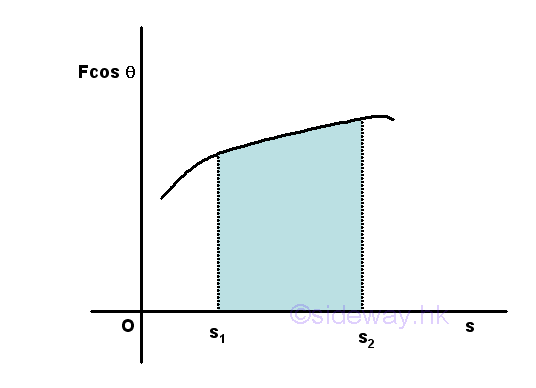
Similarly, an infinitesimal work done by a couple of forces of moment M acting on a body with an differential angular displacement can be expressed as the scalar product of the force vector and the angular differential displacement vector. The work of a force acting on a particle along a curve can be obtained by integration over the angle of rotation during the finite rotation of the body. Imply
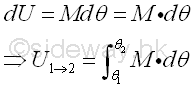
Conservative Force
By definition, the work done by a conservative force with an displacement between two points 1 and 2 is indepentent of the path of travelling between the two points. When considering the work done of any closed return path of moving from point 2 to point 1 as the reverse sense of the work done of one path moving from point 1 to point 2, the net work done is equal to zero.
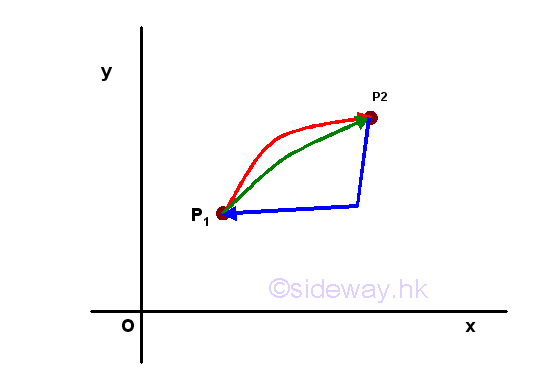
In other words, when a body is subjected to a conservative force system, the body can be considered to be within an analytic conservative force field in which the energy of the body moving from one position to another is not dependent on the travelling path of moving the body from the initial position within the field before reaching the final position, but dependent on the initial and final positions of the body in the field. Therefore, in a conservative force system, the conservative force at every position is a determinable force vector of single-valued.
Non-Conservative Force
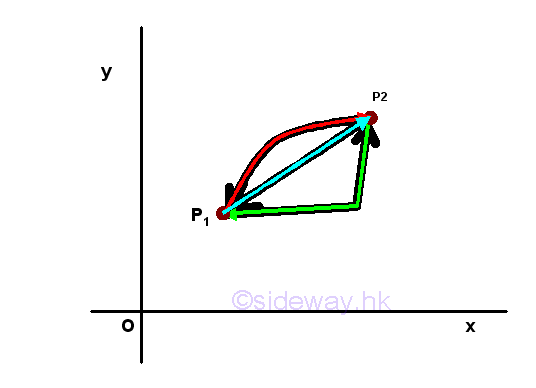
There are also non conservative forces. For example, a body on a xy plane, since the value of friction force acting on a body at a given position may have different values in magnitude and direction according to the path of travelling, the work done by friction force while the body moving from poistion one to position 2 does dependent upon the path of travelling and is not reversible. the friction force in a force field system is not a conservative force and the system becomes a non-conservative force field system.
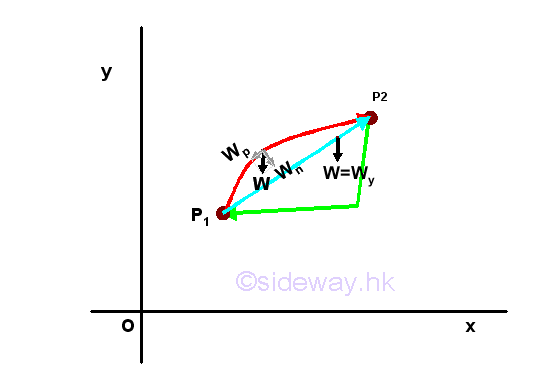
Work of Conservative Weight
The weight of a body is one the most common conservative force of the gravitational force field system. For example, a body of W on a vertical xy plan, the weight of the body can be decomposite into the force, Wn normal to the motion and the force Wp parallel to the motion. Since work done is equal to the scalar dot product of the two vector, only the force parallel to the motion does work, and the force normal to the motion does no work and is called nonworking force. And similarly if the weight of the body is decomposited into the coordinate components Wx and Wy. The horizontal component of the weight should be equal to zero, and no work can be done. While the vertical component of the weight does work along the vertical displacement is the total work done by the weight. The work of weight exerted on the body along a curve can be obtained by integration over the vertical displacement of the body. Since the force, weight is always pointing downward with the tendency to move the body to a lower energy potential while the y axis is positive when pointing upward, a negative sign is added to imply that a force of the same magnitude W is needed to be applied in the opposite direction to move the body upward along the vertical displacement because the weight acting on a body will move the body downward in nature. Imply
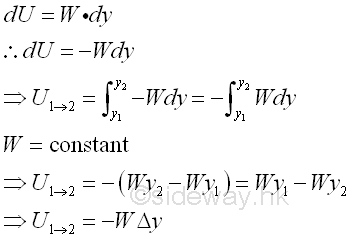
Graphically, the magnitude of the definite integral of work done by the weight of a body along the travelled path can be represented by the area under the curve of the graph of W again y in an xy plane for a homogeneous gravitational force field, the work of weight is
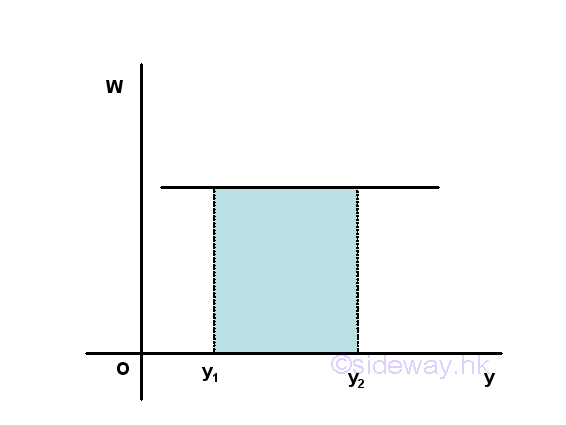
Work of Conservative Spring Force
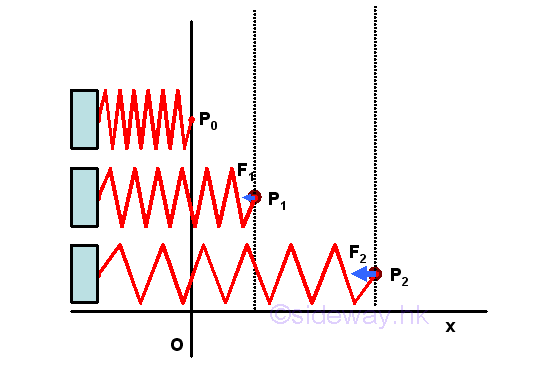
Another common conservative force used in mechanic design is the elastic force field system exerted by a spring. For example, a straight extension spring of spring constant k on a xy plan, the magnitude of force exerted by the spring at a reference point is proportional to the deflection x of the spring measured from the undeformed position, i.e. F=kx. As in the gravitational force field system, the force exerted by the spring on a body is always opposite to the finite displacement of the reference point, a negative sign is added to imply that a force of the same magnitude F is needed to be applied in the opposite direction to move the body forward along with the displacement of the deflection because the force acting on a body will move the body return backward to the reference point in nature. Imply
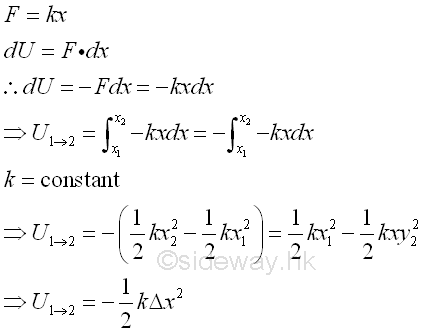
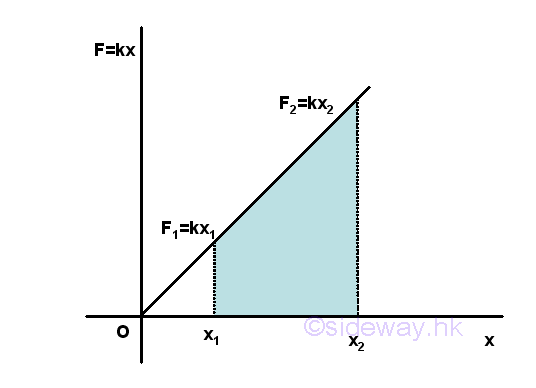
Graphically, the magnitude of the definite integral of work done by the force of a spring along the travelled path can be represented by the area under the curve of the graph of F again x in an xy plane for a elastic force field, the work of spring is
Potential Energy
In a conservative force field, the work done on a body by the conservative force can be expressed as a function of position of the body in term of the work done during the displacement the body from the reference datum position to the present position. Therefore, the work done on a body located at the reference datum in a conservative force field is equal to zero. The term potential energy of a body is used to describe the amount work done by the conservtive force to the body in a conservative force field at the position relative to the reference datum. For example, in a gravitational force field, let Vg be the gravitational potential energy at position y , imply the relation between the work done during a displacement and the change in gravitational potential energy is
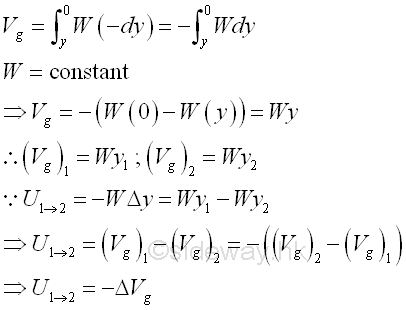
Simlary, for the elastic force in a elastic force field, let Ve be the elastic potential energy at position x , imply the relation between the work done during a displacement and the change in elastic potential energy is
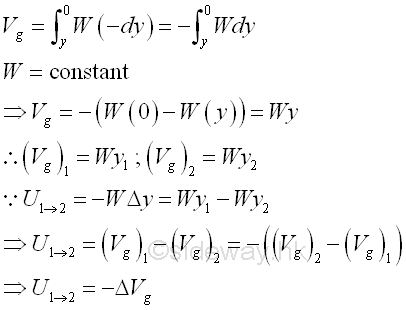
When a force is conservative in a conservative force vector field F, a function V called potential energy can always be found such that F=-∇V. Or in terms of differential forms, any force F other than gravity forces and elastic forces, e.g. applied force A is conservative when the elementary work of the force considered is an exact differential. The potential energy V of a body in a system of conservative forces may receive all available potential energies in the conservative system. For example, the potential energy V of a body under gravitational force, spring force and applied force is equal the sum of the gravitational, elastic and applied potential energies exerted on the body. Imply
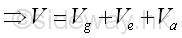
The potential energy exerted on a body does no work on the body when there is no displacement. And work is received by the body from the conservative forces acting on the body in the conservative force field when the body undergoes a displacement. And in terms of the potential energy function, the differential work done by all conservative forces during a differential displacement is equal to the negative of the differential change of the potential energy of the body due to the corresponding differential displacement of the body. As in the virtual work, the virtual displacement of a body in the conservative forces field will also cause a virtual change in the potential enegy of the body accordingly. Imply
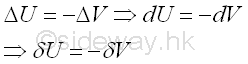
Equilibrium
Since the potential energy function of a body in the conservative force field is only dependent on the position, for example, the potential energy function of the body in the conservative force field system is a function of a single variable θ for a single degree of freedom system. Therefore the virtual differential change of the potential energy due to the virtual differential displacement can be expressed in term of the derivative of the potential energy function with respect to the variable θ at that point. Imply
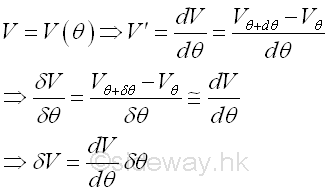
When the body is in equilibrium, the virtual work done by all forces acting on it is equal to zero. Therefore the virtual differential potential energy change due to the virtual differential displacement is equal to zero also. Imply
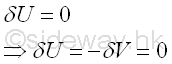
As the virtual differential displacement is not equal to zero, the derivative of the potential energy function with respect to the position variable θ at that point must be equal to zero. Imply
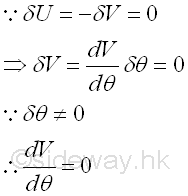
Therefore, when a body is in equilibrium in a conservative forces field, the derivative of the potential energy function of the body with respect to the position variable θ is equal to zero. Similarly, if the potential energy function is a function of n independent position variables, θ1, θ2, θ3, ... θn, that is n degrees of freedom system, when the body is in equilibrium, the virtual work done by all forces acting on it is still equal to zero. Therefore the virtual differential potential energy change due to the virtual differential displacement is equal to zero also. Since these position variables are independent variables of each other, the partial derivatives of the potential energy function with respect to each independent variable must be equal to zero when the body is in equilibrium. Imply
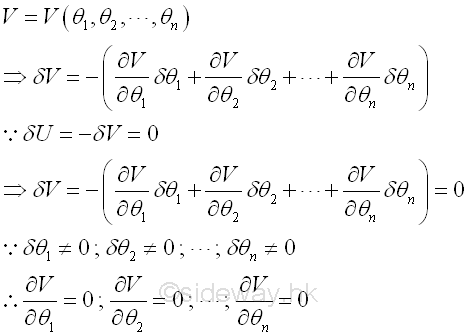
Example of Potential Energy in Equilibrium
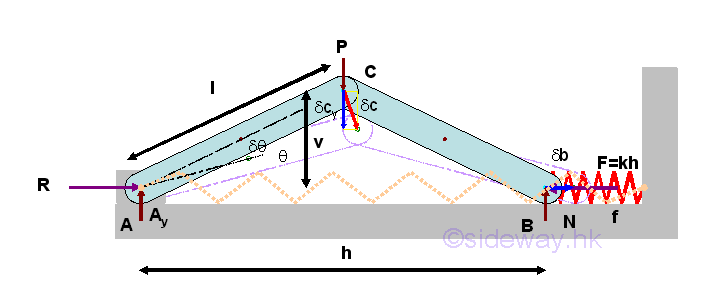
When the whole mechanism is in equilibrium, the compression is compressed by h measured from its undeformed position. The two independent positions can be expressed in term of the angle θ. Imply
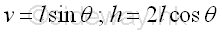
The potential energy function of the spring is
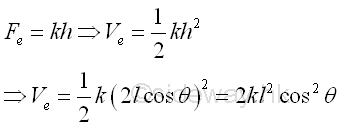
An applied force P is a conservative force. The potential energy function of the applied force P can be determined by the natural equilibrium position of the system where the work done by the applied force P is equal to zero, i.e. displacement equals to zero. Imply
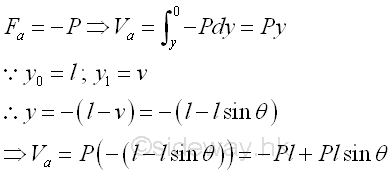
The total potential energy of the body is
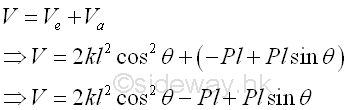
when the body is in equilibrium, the derivative of the potential energy function with respect to the angle θ is equal to zero. Imply
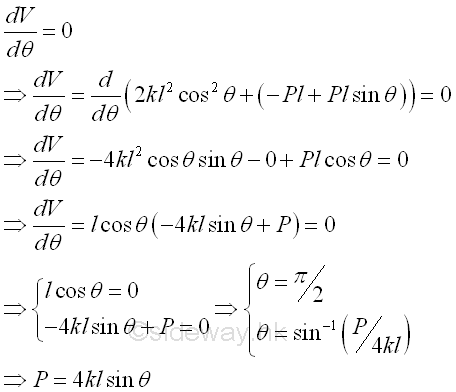
The relation between the applied force P and the spring constant or the spring force can be obtained. And the possible position of the body in equilibrium are at θ = π/2, i.e. the natural position of the body without the applied force and at θ =cos-1(P/4kl), i.e. the balanced position of the body at which the applied force is balanced by the spring force.
Stability of Equilibrium
In the example of the applied force and spring system, whenever there is small change in the angle θ, the conservative forces in the force field will restalled the system into the equilibrium position. In general, there are three types of equilibrium, they are the stable equilibrium, unstable equilibrium, and neutral equilibrium.
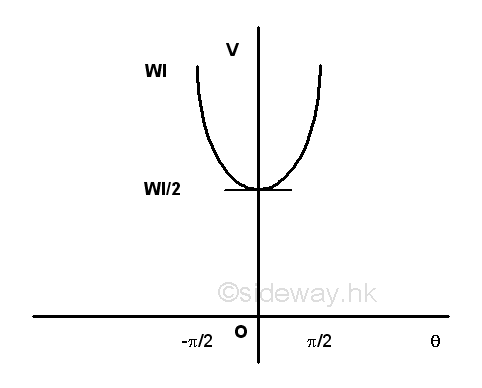
For example, a stable equilibrium at θ=0 of a pin supported bar supported at its upper part.
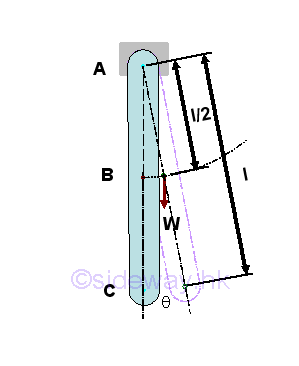
Taking point C as the datum, the potential energy of the body in terms of angle θ is.
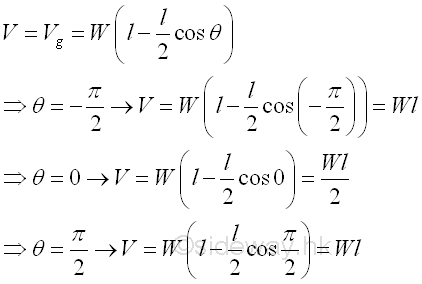
Graphically, the potential energy of the body against the angle θ is.
For example, an unstable equilibrium θ=0 of a pin supported bar supported at its lower part.
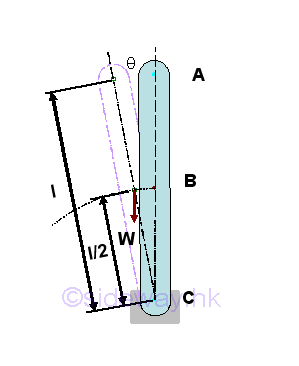
Taking point C as the datum, the potential energy of the body in terms of angle θ is.
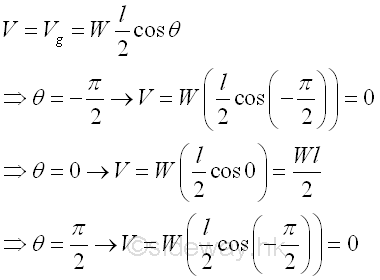
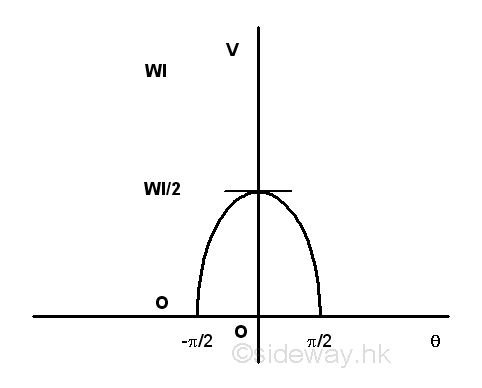
Graphically, the potential energy of the body against the angle θ is.
For example, a neutral equilibrium θ=0 of a pin supported bar supported at its middle part.
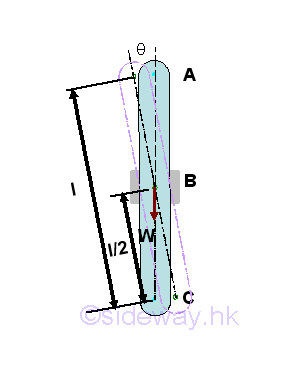
Taking point C as the datum, the potential energy of the body in terms of angle θ is.
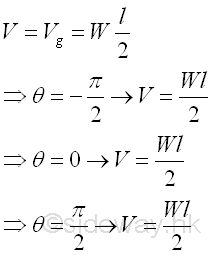
Graphically, the potential energy of the body against the angle θ is.
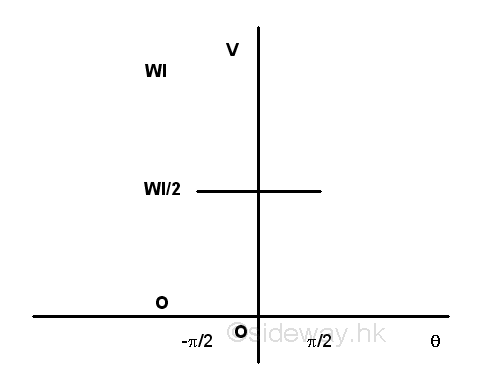
According to the graph, the potential energy of the bar in stable equilibrium is minimum, while the potential energy of the bar in unstable equilibrium is maximum and the potential energy of the bar in neutral equilibrium is constant. Generally, the conservative forces in the conservative force field always try to decrease the potential energy of the body by doing positive work to the body. Since the curve in the graph is a function of angle θ, the conditions of a function is maximum, minimum or constant in calculus can also be applied to the function of potential energy. Imply

And by Taylor's series expansion, the pontential energy function V(θ) about the equilibrium position θo is
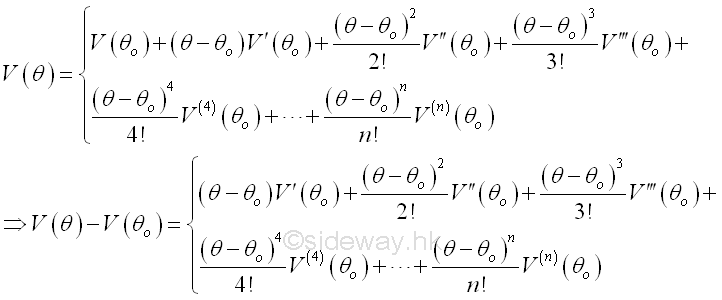
Since (θ-θo) can be positve or negative, i.e. on the two sides of the equilibrium position, therefore when the first and second derivatives of the potential energy function is equal to zero, if the first non-zero higher order derivative is of even order and greater than zero, then V(θ)-V(θo) is always greater than zero, imply the potential energy at the equilibrium position, θo, is minimum and the equilibrium is stable equilibrium, other the equilibrium is unstable.
And applying Taylor's theorem similarly, for a two degree of freedom conservative system with independent variables, θ1, and θ2, the equilibrium of styemt is stable when the potential energy is minimum also. And the conditions for a stable equilibrium are.
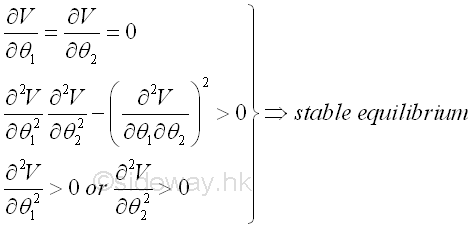
©sideway
ID: 121200002 Last Updated: 12/15/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
