Content
Limit
Concept of
Limit
Limit of a Sequence
Limit of a Decreasing Sequence
Limit of an Increasing Sequence
Limit of a Non-monotonic Sequence
Limit of a Series
Limit
The term "limit" refers to the functional value of a functon when approaching a point of position on the function even the point might not exist.
Concept of Limit
The concept of limit applied in Calculus is also based upon the limit of a sequence and the limit of a series.
For example, the distance to destination problem. When an object moves at a constant velocity s/2 per n from A to B of distance s apart, the distance to destination x can be determined by the equation x=s-ns/2. At n=2, the object will reach the destination A. The solution is a rational number. But if the object moves at a constant velocity 3s/10 per n from A to B of distance s apart. the distance to destination x can be determined by the equation x=s-3ns/10. Then at n=3.333..., the object will reach the destination A. The solution is a irrational number. However when an object moves at a constant ratio of half of the distance to distination, 0.5x per n from A to B of distance s apart, the distance to destination x can be determined by the equation x=s(1/2)n. At n=2, the object is at s/4 away from B. At n=3, the object is at s/8 away from B. As n increase, the object move closer to B, but the object will never reach the destination B because there is alway another half of the distance remained. The numbers of the distance to distination B on each trial form an infinite sequence, i.e. 1/2, 1/4, 1/8, ..., 1/2i, ...1/2n, .... However for any small quantity of the distance to B, there is always a corresponding n such that the distance to B is smaller than the specified small quantity. Since the destination B is still the destination of the object and therefore the "limit" of the function of object distance from B is zero when n tends to infinity. This is the approaching of the limit by taking independent value tends to infinity.

Another typical example is the area of a circle. Area of a circle can be estimated by inscribed polygons through summation of areas of triangles. For example a circle of radius r
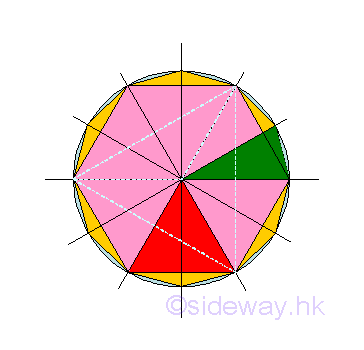
At first trial, the area of a circle is approximated by a trigon. The number n of triangles to form the polygon is 3. The height h of the triangle is 0.5r and the base b of the triangle is 1.732r. Area of circle is estimated to be 1.299038r2. Since the relations of height and base between two polygons by doubling the number of sides can be determined by pythagorean theorem, the successive trial is hexagon for a trigon. Imply
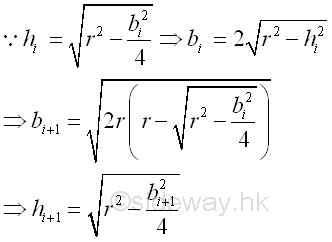
At second trial, the area of a circle is approximated by a hexagon. The number n of triangles to form the polygon is 6. The height h of the triangle is 0.866r and the base b of the triangle is r. Area of circle is estimated to be 2.598076r2. At third trial, the area of a circle is approximated by a dodecagon. The number n of triangles to form the polygon is 12. The height h of the triangle is 0.966r and the base b of the triangle is 0.518r. Area of circle is estimated to be 3r2. For more trial, the number of sides of the polygon increases, the area of the polygon becomes a better approximation to the area of the circle, but the area of the polygon will never be the area of the circle because there is alway another polygon can be constructed by doubling the number of sides of polygon. The numbers of the area of polygon on each trial form an infinite sequence, i.e. 1.299038r2, 2.598076r2, 3r2, ...3.141558r2, ...3.141593r2, .... However for any small quantity of improvement on better approximation to the area of the circle, there is always a corresponding trial such that the difference between the area of polygon and the area of circle is smaller than the specified small quantity. Since the target of the approximation is to estimate the area of the circle and therefore the "limit" of the function of the area of polygon approximation is the area of the circle when the trial i tends to infinity. This is the approaching of the limit by taking independent value, trial i, tends to infinity.
When considering the area of triange, as the number of trial increases, the area of triange decreases and the base of the triangle also descrease accordingly. The area of triangle with smaller base becomes a better approximation to the area of the circle. However the area of triangle will never be equal to zero also because there is always another triangle can be constructed by reducing the length of the triangle base. Similarly, the numbers of the area of triangle on each trial form an infinite sequence, i.e. 0.433013r2, 0.433013r2, 0.25r2, ...0.004091r2, ...0.000064r2, .... However for any small quantity of improvement on better approximation to the area of the circle, there is always a corresponding smaller triangle such that the difference between the area of polygon and the area of circle is smaller than the specified small quantity. Since the target of the approximation is to estimate the area of the circle and therefore the "limit" of the function of the area of polygon approximation is the area of the circle when the area of triangle tends to zero. This is the approaching of the limit by taking independent value, area of triangle, tends to zero. The area of triangle should not be equal to zero otherwise the area of polygon will be equal to zero and the point at the area of triangle equals to zero does not exist.
Limit of a Sequence
In general, the output functional value y of a function f(x) can be arranged in an sequence according to the order of the input independence variable x when the domain of independence variable x is limit to positive integer only. For an infinite sequence of functional values, i.e. a1, a2, ..., ai, ..., an, ..., if there is a number A, such that |A-an|<ε, for an and all numbers after an, then A is the limit of the infinite sequence. Imply
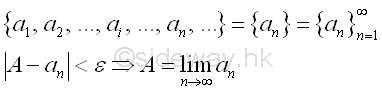
where ε can be any assigned positive number, an is the n term of the sequence, and |A-an| is the absolute value of (A-an).
Therefore, for a number an, if A>an then A-ε<an and if A<an then A+ε>an. In other words, the limit of the sequence is A if the number an and all numbers after an are greater than (A-ε) and less than (A+ε) , that is the values of numbers are limited within a range of ±ε. Graphically, the point an and all points after an in the sequence lie on the line segment between (A-ε) and (A+ε) of the number line. Imply
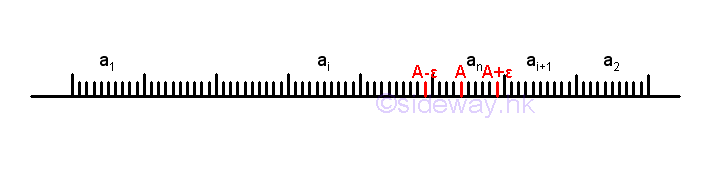
For an infinite sequence, although there are many numbers before the number an, the numbers of points before the point an are finite, but the numbers of points after the point an are infinite.
Limit of a Decreasing Sequence
For a monotonically decreasing infinite sequence from a monotonically decreasing function, i.e. a1, a2, ..., ai, ..., an, ..., each term in the sequence is always smaller than or equal to the previous term. If there is a number M, such that M is smaller than all numbers in the sequence, then the sequence must have a "limit" A. Graphically, all points of the infinite sequence lie on the number line from right to left orderly, and point M is located the leftmost of number line next to the sequence of points. Imply
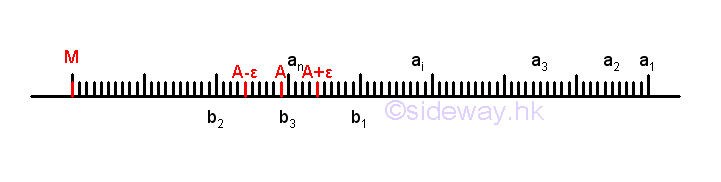
Since M and a1 are the first and last numbers on number line, all points lie on the line segment Ma1 only. Method of number line bisection can be used to reduce the number of sequence points by retaining the line segment with infinite number of points because the limit of the sequence must be on the line segment with infinite number of points. For example, the line segment Ma1 is bisected at b1 and line segment Mb1 has infinite number of points. Then the line segment Mb1 is bisected at b2 and line and line segment b2b1 has infinite number of points. And then the line segment b2b1 is bisected at b3 and line segment b2b3 has infinite number of points. By repeating the bisection of the line segment with infinite number of points, the length of the line segment containing the limit can be reduced to any very small quantity that is tending to zero and without actually being zero. Therefore for any specified small quantity ε, there is always a corresponding line segment on the number line such that the number an and the numbers of points after the point an on the sequence fulfil the criteria of limit exist, i.e. |A-an|<ε .
For example:
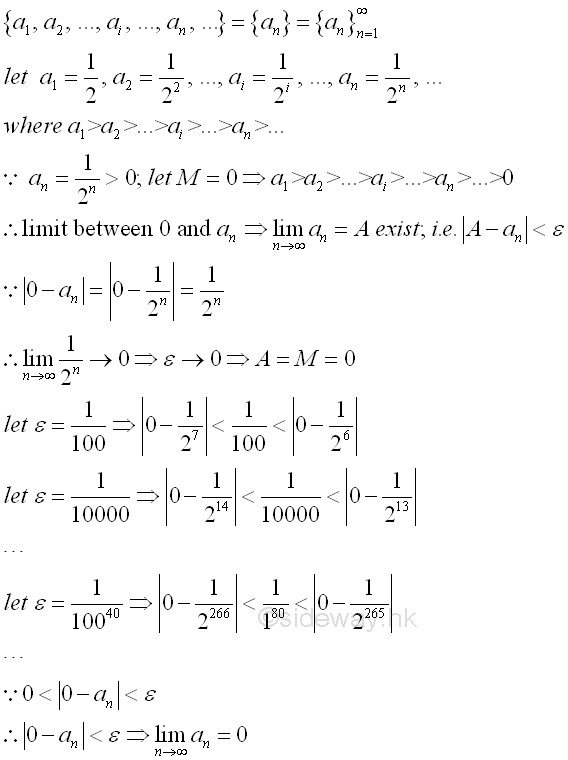
Limit of an Increasing Sequence
For a monotonically increasing infinite sequence from a monotonically increasing function, i.e. a1, a2, ..., ai, ..., an, ..., each term in the sequence is always larger than or equal to the previous term. If there is a number M, such that M is larger than all numbers in the sequence, then the sequence must have a "limit" A. Graphically, all points of the infinite sequence lie on the number line from left to right orderly, and point M is located the rightmost of number line next to the sequence of points. Imply
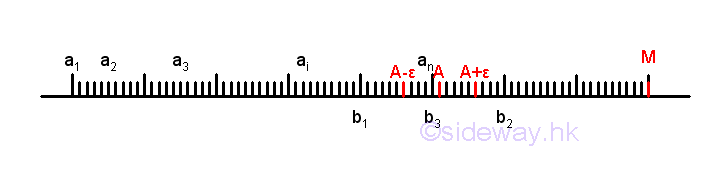
Since M and a1 are the first and last numbers on number line, all points lie on the line segment Ma1 only. Method of number line bisection can be used to reduce the number of sequence points by retaining the line segment with infinite number of points because the limit of the sequence must be on the line segment with infinite number of points. For example, the line segment Ma1 is bisected at b1 and line segment Mb1 has infinite number of points. Then the line segment Mb1 is bisected at b2 and line and line segment b2b1 has infinite number of points. And then the line segment b2b1 is bisected at b3 and line segment b2b3 has infinite number of points. By repeating the bisection of the line segment with infinite number of points, the length of the line segment containing the limit can be reduced to any very small quantity that is tending to zero and without actually being zero. Therefore for any specified small quantity ε, there is always a corresponding line segment on the number line such that the number an and the numbers of points after the point an on the sequence fulfil the criteria of limit exist, i.e. |A-an|<ε .
For example:
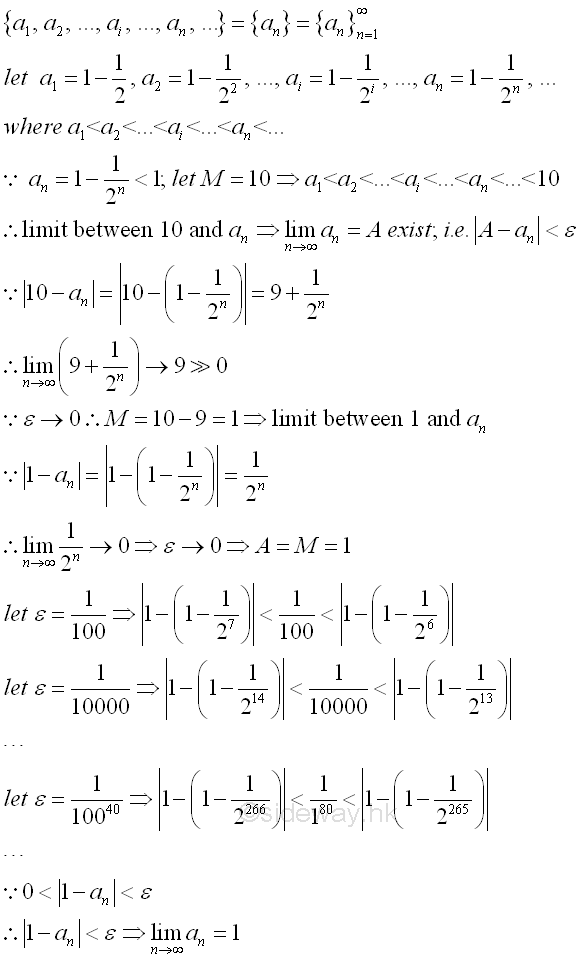
Limit of a Non-monotonic Sequence
For a non-monotonic infinite sequence from a non-monotonic function, i.e. a1, a2, ..., ai, ..., an, an+1, ..., an+p, .... If there is a number an, such that |an+p-an|<ε for all numbers an+p after an in the sequence where p is a integer, then the sequence must have a "limit" A. All numbers after an are greater than (an-ε) and less than (an+ε). Graphically, all points of the infinite sequence lie on the number line, and the limit A is located in between the sequence of points. Imply
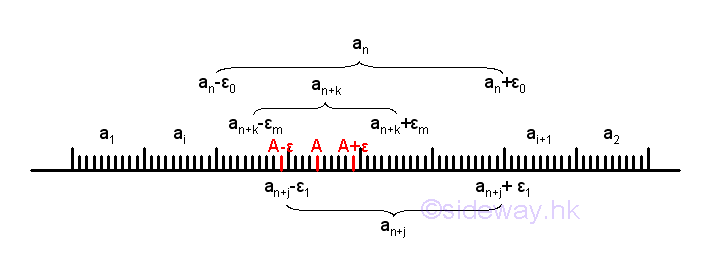
A non-monotonic sequence can be considered as a combination of the trends of decreasing and increasing and a non-monotonic sequence and is the general case of a sequence. Since all numbers an+p after an in the sequence are greater than (an-ε) and less than (an+ε), there is alway an equivalent line segment on the number line including all infinite points of number an and all numbers an+p after an in the sequence. For example, let the initial small quantity ε be ε0 and the number an where p=0, such that |an+p-an|<ε0 for all numbers an+p after an in the sequence. If a smaller small quantity ε1 is specified, there is always an equivalent smaller line segment, such that |an+p-an+j|<ε1 on the number line including all infinite points of number an+j and all numbers an+p after an+j in the sequence. Although the infinite numbers on the line segment ε1 is also contained in the infinite numbers on the line segment ε0, the line segment ε1 may be part of the line segment ε0, or the two line segments may be overlapped each other. Since n+j is always greater or equal to n, the number of infinite numbers in the sequence is reduced. In general, for any specified smaller small quantity εm, there is always an equivalent smaller line segment, such that |an+p-an+k|<εm on the number line including all infinite points of number an+k and all numbers an+p after an+k in the sequence. By repeating the process, the length of the line segment containing the limit can be reduced to any very small quantity that is tending to zero and without actually being zero. Therefore for any specified small quantity ε, there is always a corresponding line segment on the number line such that the number an+p and the numbers of points after the point an+p on the sequence fulfil the criteria of limit exist. i.e. |A-an+p|<ε.
For example:

Limit of a Series
Similarly, since the output functional value y of a function f(x) can be arranged in an sequence according to the order of the input independence variable x when the domain of independence variable x is limit to positive integer only. The sum of the output functional value y of a function f(x) can also be arranged in an infinite series according to the order of the input independence variable x when the domain of independence variable x is limit to positive integer only. For example, an infinite series of the sum of functional values, i.e. a1+a2+...+ ai+...+an+..., let sn be the sum of the n term of the series, i.e. sn=a1+a2+...+ ai+...+an. Then the corresponding partial sum of the series can be arranged as an sequence according to the order of numer of terms in the series, i.e. s1, s2, ..., si, ..., sn, .... If the sequence has a limit A, then the infinite series is called convergent series and A is the sum of the infinite series. Imply
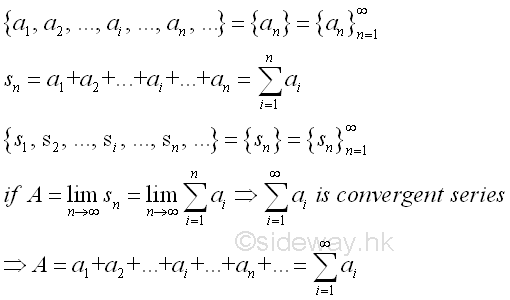
Unlike sequence, if the series is convergence, the last term in the series when tending to infinity should be approaching zero. Therefore the existing of a limit for an infinite series can also be determined by the convergency of the infinite sequence by examinating two successive terms of the infinite sequence. Similar to the limit of an infinite sequence, for any specified small quantity ε, there is always an index n such that the difference between the number an and the previsous number an-1 on the sequence fulfil the criteria of limit exist. i.e. |an-an-1|<ε. And therefore the n term in the series when tending to infinity should be approaching zero.
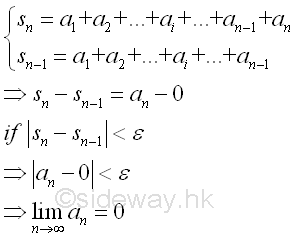
For example:
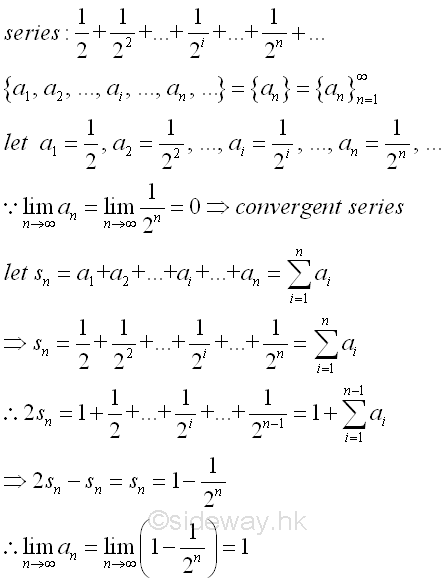
©sideway
ID: 130100002 Last Updated: 1/17/2013 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
