Content
Primality
The Porperty of Mann and Shanks (1972)[1,3]
The Prime
Power Dividing a Factorial (1808)[1]
The Prime
Power Dividing a Binomial Coefficient (1852)[1]
Primality
Prime numbers are natural numbers, e.g. 2, 3, 5, 7,..., which can only be divided by 1 and itself. Although the way to recognize the primality of a natural numbe is very simple, there is difficulty of distinguishing prime numbers from composite numbers when natural numbers become very large.
The Porperty of Mann and Shanks (1972)[1,3]
Another property of prime related to binomial coeffiecent is the property of
Mann and Shanks characterized by the divisibility of the binomial coefficients
relatived to a prime number p in the specified manner. Instead of focusing on
one individual set of binomial coefficients, Mann and Shanks checks the
divisibility of multiple sets of the binomial coefficients relatived to a
prime number p. In order to visualize the relationship, Mann and Shanks tabulate
the Pascal's Arithmetical Triagle by shifting the starting column of each row two places to the right
relative to the prievious row. In other words, the row n of binomial
coefficient with power index n is placed between columns 2n and 3n inclusive. Column number p is a prime number
if and only if row number k divides (k
p-2k) for every largest integer k such that ⌊(p+2)/3⌋, ⌊(p+2)/3⌋+1,...,⌊p/2⌋.
| n\p | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||||||||||||||||||||||||||||
| 1 | 1 | 1 | |||||||||||||||||||||||||||||||
| 2 | 1 | 2 | 1 | ||||||||||||||||||||||||||||||
| 3 | 1 | 3 | 3 | 1 | |||||||||||||||||||||||||||||
| 4 | 1 | 4 | 6 | 4 | 1 | ||||||||||||||||||||||||||||
| 5 | 1 | 5 | 10 | 10 | 5 | 1 | |||||||||||||||||||||||||||
| 6 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||||||||||||||||||||||||
| 7 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||||||||||||||||||||||||
| 8 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | ||||||||||||||||||||||||
| 9 | 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | |||||||||||||||||||||||
| 10 | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | ||||||||||||||||||||||
| 11 | 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | |||||||||||||||||||||||
| 12 | 1 | 12 | 66 | 220 | 495 | 792 | 924 | 792 | |||||||||||||||||||||||||
| 13 | 1 | 13 | 78 | 286 | 715 | 1287 | |||||||||||||||||||||||||||
| 14 | 1 | 14 | 91 | 364 | |||||||||||||||||||||||||||||
| 15 | 1 | 15 | |||||||||||||||||||||||||||||||
The binomial coefficients for each row in term of row number n is (n
i) where k=0,1,2,...n. Or in term of column number p is (p/2
i) where i=0,1,2,...p/2., since p/2=n. From the table, the only
possible column p such that the whole column of the binomial coefficients are
divisible by the first row number index is equal to n*2+n-1=p with binomial
coefficient (n
n-1) or m*2+m-2=p with binomial coefficient (m
m-2) for n,m>2. In other words, the first row number is equal
k=⌊(p+2)/3⌋ and the binomial coefficient is equal to (k
p-2k). Similarly, the possible whole column of the binomial coefficients are divisible
by the last row number index is equal to n*2+1=p with binomial coefficient (n
1). In other words the last row number
index n is equal to n=(p-1)/2 or k=⌊(p)/2⌋. the binomial
coefficient is equal to (k
p-2k), Therefore the property can be specified as before.

For prime number p greater than 3, the row number index p can be expressed as
p=6k+1=3n-2 or p=6k-1=3n-1. Consider p=6k+1=3n-2, imply n=2k+1 and the
corresponding binomial coefficients in the column is (2k+i
3i-1). where the row index i=1,2,...,k. Since the
two binomial coefficients of successive rows are (2k+m-1
3m-4), and (2k+m
3m-1) ), imply (2k+m-1
3m-2)(2k+m)=(2k+m
3m-1)(3m-1). If row number 2k+m does not divide the binomial
coefficient, then gcd(2k+m,3m-1)>1. Therefore gcd(6k+3m,3m-1)>1 , imply
(6k+1,3m-1) or (p,3m-1)>1. In other words p is divisible and p is not a
prime number. Therefore if p is a prime number, each binomial coefficients in
the same column must be divisible by its row number. Similarly, if p=6k-1=3n-1,
imply n=2k and the corresponding binomial coefficients in the column is (2k+i
3i+1). where the row index i=0,1,2,...,k-1. Since the two
binomial coefficients of successive rows are (2k+m-1
3m-2), and (2k+m
3m+1) ), imply (2k+m-1
3m)(2k+m)=(2k+m
3m+1)(3m+1). If row number 2k+m does not divide the binomial
coefficient, then gcd(2k+m,3m+1)>1. Therefore gcd(6k+3m,3m+1)>1 , imply
(6k-1,3m+1) or (p,3m+1)>1. In other words p is divisible by 3m+1 and p is not a
prime number. Therefore if p is a prime number, each binomial coefficients in
the same column must be divisible by its row number.

Since all even column number p have a non divisible binomial coefficients for (p
0), all even column number p is not a prime. For all odd composite column
number p=s(2t+1) where s is prime factor and t≥1. Let row number n=st where n
does not divide the binomial coefficient at column p. The binomial coefficient
at n row and p column is (st
s)=t(st-1
s-1) , therefore ther row number n=pk does not divide the binomial
coefficient.
The Prime Power Dividing a Factorial (1808)[1]
In 1808, Legendre determined the exact prime power pm
that divideds a factorial a! and m can also be expressed in terms of the p-adic
development of a, that is ((a-(a0+a1+a2+a3+...+ak))/(p-1). By definition a!=pmb, where p∤b. Let a>p, then a=q1p+r1 with 0≤q1, 0≤r1<p. Imply q1=⌊a/p⌋.
For multiples of p not bigger than a, i.e. p,2p,...q1p≤a,
then by definition, pq1(q1!)=pmc where p∤c
as a is divided into q1 segments.
Let m=q1+n1, then pq1(q1!)=pq1+n1c or pn1
divides q1!. For each 1≤i≤k,
there are ⌊q1/pi⌋-⌊q1/pi+1⌋ numbers between 1 and q1
is divided by the greatest power i of p only. So the greatest power of p
dividing q1! is
∑ k
i=1 i(⌊q1/pi⌋-⌊q1/pi+1⌋)=∑ k
i=1 (⌊q1/pi⌋). Therefore
n1 is equal to
⌊q1/p1⌋+⌊q1/p2⌋+.... Since
⌊q1/pi⌋=⌊⌊a/p⌋/pi⌋=⌊a/pi+1⌋, imply
n1=⌊a/p2⌋+⌊a/p3⌋+⌊a/p4⌋+.... From
m=q1+n1, imply m=⌊a/p⌋+n1=⌊a/p1⌋+⌊a/p2⌋+⌊a/p3⌋+⌊a/p4⌋+....

Let a=akpk+...+a1p+a0. where pk≤a<pk+1
and 0≤ai≤p-1 for i=0,1,...,k. Then ⌊a/p⌋=akpk-1+...+a2p+a1, ⌊a/p2⌋=akpk-2+...+a3p+a2, ..., ⌊a/pk⌋=ak,
Therefore m=∑ k
i=1 (⌊q1/pi⌋) can be
expressed as (akpk-1+...+a2p+a1)+(akpk-2+...+a3p+a2)+(akpk-3+...+a4p+a3)+...+(ak)=
a1+a2(p+1)+a3(p2+p+1)+...+(ak)(pk-1+pk-2+...+p+1)=
((a1(p-1)+a2(p2-1)+a3(p3-1)+...+ak(pk-1))/(p-1)=
((a1p+a2p2+a3p3+...+akpk)-(a1+a2+a3+...+ak))/(p-1)=
(a-(a0+a1+a2+a3+...+ak))/(p-1).
and is equal to the p-adic valuation of a!

The Prime Power Dividing a Binomial Coefficient (1852)[1]
In 1852,
Kummer extends the Legendre's result to determine the exact prime power pm
that divideds a binomial coefficient (a+b
a)=(a+b)!/a!b!, where a≥1,b≥1. Similar to Legendre, Let
a=atpt+...+a1p+a0. and b=btpt+...+b1p+b0. where 0≤ai≤p-1
and 0≤bi≤p-1 for i=0,1,...,t. with either at≠0 or
bt≠0. Let Sa=∑ t
i=0ai, Sb=∑ t
i=0bi
be the sums of p-adic digits of a, b. Let ci be 0≤ci≤p-1 and εi=0
or 1. such that a0+b0=ε0p+c0, ε0+a1+b1=ε1p+c1, ε1+a2+b2=ε2p+c2, ..., εt-1+at+bt=εtp+ct.
Therefore c0=a0+b0-ε0p, c1=ε0+a1+b1-ε1p, c2=ε1+a2+b2-ε2p, ..., ct=εt-1+at+bt-εtp.
Or (c0+c1+c2+...+ct)= ((a0+a1+a2+...+at)+(b0+b1+b2+...+bt))+(ε0+ε1+...+εt-1)-(ε0p+ε1p+ε2p+...+εtp)=
((a0+a1+a2+...+at)+(b0+b1+b2+...+bt))+(ε0+ε1+...+εt-1+εt)-(ε0p+ε1p+ε2p+...+εtp)-εt=
((a0+a1+a2+...+at)+(b0+b1+b2+...+bt))+(ε0+ε1+...+εt-1+εt)(1-p)-εt. By multiplying
all equations with 1,p,p2,...pt
.accordingly, imply a0+b0=ε0p+c0, (ε0+a1+b1)p=(ε1p+c1)p, (ε1+a2+b2)p2=(ε2p+c2)p2, ..., (εt-1+at+bt)pt=(εtp+ct)pt. After adding all equations together, imply
a+b+(ε0p+ε1p2+...+εt-1pt)=(ε0p+ε1p2+...+εt-1pt+εtpt+1)+(c0+c1p+c2p2+...+ct-1pt-1+ctpt). Therefore a+b=(c0+c1p+c2p2+...+ct-1pt-1+ctpt+εtpt+1)
and is equal to the expression of a+b in the base p. Similar to Sa, Sb, Sa+b=∑ t
i=0(ci)+εt. But when adding all
equations only, then a0+b0+ε0+a1+b1+ε1+a2+b2+...+εt-1+at+bt=ε0p+c0
+ε1p+c1+ ε2p+c2+...+εtp+ct. imply a0+a1+a2+...+at+b0+b1+b2+...+bt+ε0
+ε1
+...+εt-1=(ε0+ε1+
ε2+...+εt)p+c0+c1+c2+...+ct.
Imply Sa+Sb+(ε0+ε1+...+εt-1)=(ε0+ε1+
ε2+...+εt)p+Sa+b-εt.
Imply Sa+Sb-Sa+b=(ε0+ε1+
ε2+...+εt)(p-1).
Since (a+b
a)=(a+b)!/a!(a+b-a)!=(a+b)!/a!b! , by Legendre prime power
pmb=a!, m(p-1)=a-(a0+a1+a2+a3+...+ak),
then (a+b)!/a!b!=(pm1c1)/((pm2c2)(pm3c3))=pmc
, imply m=m1+m2+m3
, imply m(p-1)=((a+b)-Sa+b)-(a-Sa)-(b-Sb) .
imply (p-1)m=(Sa+Sb-Sa+b)=(p-1)(`0+ε1+
ε2+...+εt) .
Imply m=(`0+ε1+
ε2+...+εt).
that is "The exact power of p dividing (a+b
a) is equal to (`0+ε1+
ε2+...+εt),
which is the number of 'carry-overs' when performing the addition of a, b,
written in the base p. This theorem of Kummer was rediscovered by Lucas in 1878.
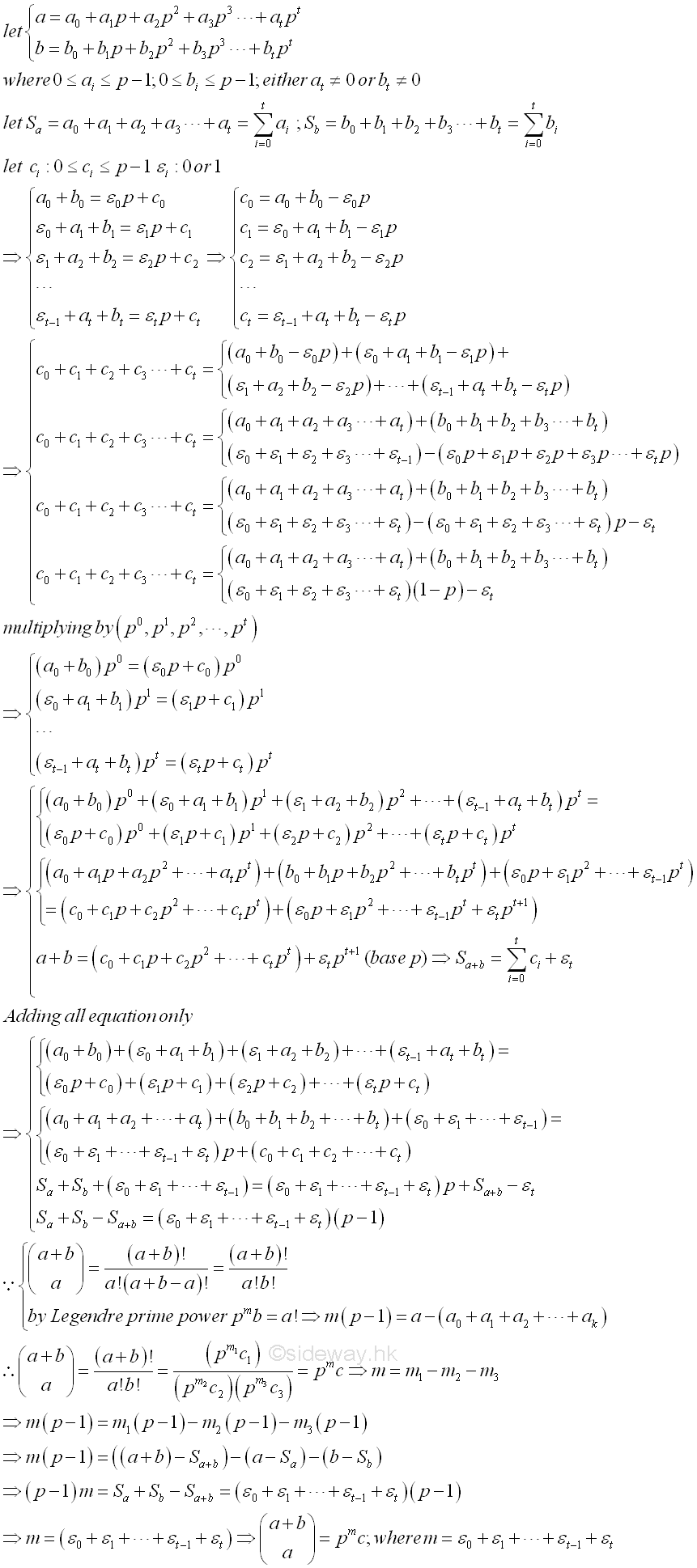
©sideway
ID: 130500001 Last Updated: 5/8/2013 Revision: 0 Ref:
References
- R. Paulo, 1996, The New Book of Prime Number Records
- Wolstenholme, R.J., 1862, On Certain Properties of Prime Numbers
- Mann, H.B., Shanks D., 1972, A Necessary and Sufficient Condition for Primality, and Its Source
- J.M Pollard, Kangaroos, 1975, A Monte Carlo Method for Factorization
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
