Content

Binomial Theorem and Binomial Series[]

A binomial is an algebraic polynomial expression of form (a+b). The binomial theorem is a theorem descibing the algebraic expansion of the powers of a binomial into an infinite binomial series.

Binomial Expansion[]

The expansion of the powers of a binomial can be obtained by direct multiplication. Imply

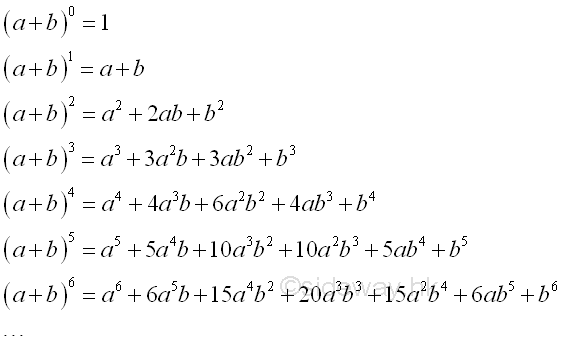
The number of terms of the binomial expansion is alway equal to the power of the binomial plus 1. The exponent of a decreases by 1 from the power of the binomial while the exponent of b increases by 1 from zero or vice versa. Therefore the first term is a to the power of the binomial and the last term is b to the power of the binomial, and the sum of the exponents of a and b is always equal to the power of the binomial. The coefficient of a is a specific integer depending on the power of the binomial and the exponent of a or b or vice versa. The coefficient of each term can be obtained by multiplying the coefficient of previous term by the exponent of a in the previous term and dividing the product by the item number of the previous term instead of direct multiplaction.

Pascal's Triangle[]

The coefficients of powers of binomial, (a+b) can be arranged in the format of Pascal triangle with the first coefficient of the powers of binomial on the same row or column.

The coefficients of powers of binomial can also be arranged in the an "equilateral" triangle pattern of same numbers of coefficients on the edge. Imply

0																	1
1																1		1
2															1		2		1
3														1		3		3		1
4													1		4		6		4		1
5												1		5		10		10		5		1
6											1		6		15		20		15		6		1
7										1		7		21		35		35		21		7		1
8									1		8		28		56		70		56		28		8		1
9								1		9		36		84		126		126		84		36		9		1
10							1		10		45		120		210		252		210		120		45		10		1
11						1		11		55		165		330		462		462		330		165		55		11		1
12					1		12		66		220		495		792		924		792		495		220		66		12		1
13				1		13		78		286		715		1287		1716		1716		1287		715		286		78		13		1
14			1		14		91		364		1001		2002		3003		3432		3003		2002		1001		364		91		14		1
15		1		15		105		455		1365		3003		5005		6435		6435		5005		3003		1365		455		105		15		1

The row number on the left is equal to the power of the binomial with the expanded binomial on the left. Similarly, the exponent of a decreases by 1 from the power of the binomial to zero while the exponent of b increases by 1 from zero to the power of the binomial or vice versa. The number of term in each row is equal to the power of the binomial plus. And the sum of the coefficient of the binomial expansion in each row is equal to 2 to the power of the power of the binomial. With this rearrangement, the coefficient of each term is equal to the sum of the two coefficients of the row above immediately. The coefficients of powers of binomial can therefore be determined by the pattern of a Pascal's triangle, rather than direct multiplication.

Properties of Pascal's Triangle

• The sum of the numbers in any row is equal to 2 to the nth power or 2n, when n is the number of the row. e.g. 24 = 1+4+6+4+1 = 16

• If the 2nd number in a row is a prime number, all the numbers in that row excluding the number 1 are divisible by the number. e.g "1 7 21 35 35 21 7 1" of row 7 are all divisible by 7 except 1.

•  The sum of the numbers of any length, i, in any diagonal is equal to the next number in the cross diagonal of a hockey stick like pattern. e.g. 1+5+15+35=56 or 1+4+10=15

• The cummulative sum of the numbers of any length, i, in a diagonal from first diagonal to is equal to the next number in next diagonal of a parallelogram pattern. e.g. (1+1+1+1+1)+(1+2+3+4+5)=21 the 6th number of third diagonal.

• The first diagonal is  a sequence of 1s.

• The second diagonal is a sequence of counting numbers, 1,2,3,4.

• The third diagonal is  a sequence of triangular numbers, 1,3,6,10....

• The fourth diagonal is a sequence of tetrahedral numbers, 1,4,10,20,35....

• The fifth diagonal is a sequence of pentatope numbers, 1,5,15,35,70,....

• The sequence of numbers after the addition of the next number to the previous number in the third diagonal is a sequence of square numbers, 1, 1+3,3+6,6+10,....

• The numbers in any row, i, is a magic 11's and is equal to 11 to the ith power by considering each number is arranged in decimal dight order. e.g. 118=214358881=1  8  28  56  70  56  28  8 1

• The sequence of numbers after the consecutive addition of the  next number of the previous row to the number in the first diagonal is a Fibonnacci's sequence, 1,  1,  1+1, 1+2, 1+3+1, 1+4+3, 1+5+6+1, 1+6+10+4.

• The numbers in any row is the numbers of figures formed by all possible lines connected by points on a circle. e.g. 7th row: 1 circle, 7 points, 21 segments, 35 triangles, 35 quadrilaterals, 21 pentagons, 7 hexagons, 1 heptagons.

•  By Harian Brothers, constant e can be calculated from the product  of consecutive multiplication of all numbers in a row and is obtained by the product of last row n+1 times the product of third last row n-1 and divided by the square of the product of the second last row when  taking limit as n approaching infinity.

• The Star of David Theorems. The product of a number in a row, the second next number in next row and the next number in second next row is equal to the product of the next number in the same row, the previous number in the next row and the next number in the third row. The greatest common divisors of these two groups of numbers are the equal

• Catalan Numbers

• Sums of the Binomial Reciprocals

• Squares

• Squares of the Binomials

• Cubes

• pi in Pascal

• Sierpinski's Triangle

Binomial Theorem[]

The binomial theorem is developed to expand binomials of any given power directly by describing the algebraic expression of the general form of a binomial expansion. The binomial theorem states that the binomial (a+x) to the power of a nonnegative integer n can be expressed as

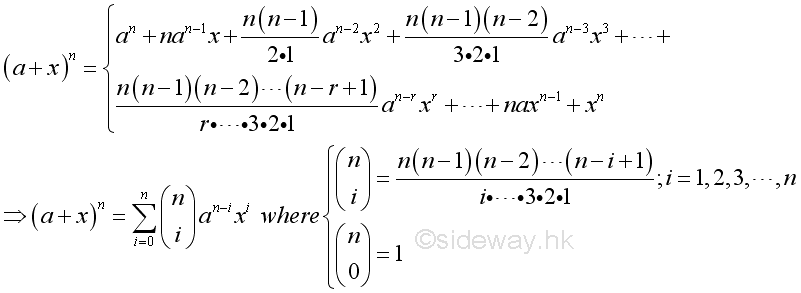
If a=1, then the general binomial series can be reduced to

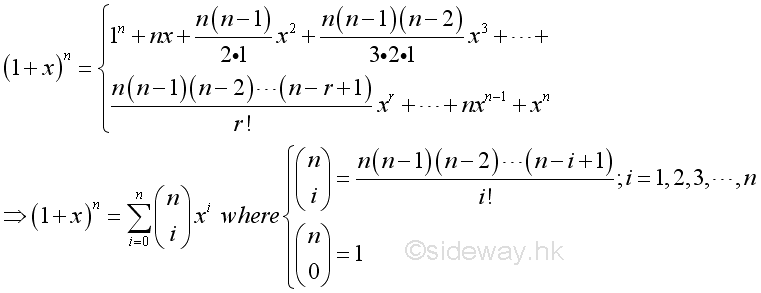
Binomial Series[]

In fact, the number n in the binomial theorem can be extended to any number. For any number n, the expansion of the binomial should be expressed in form of an infinite series, called binomial series.

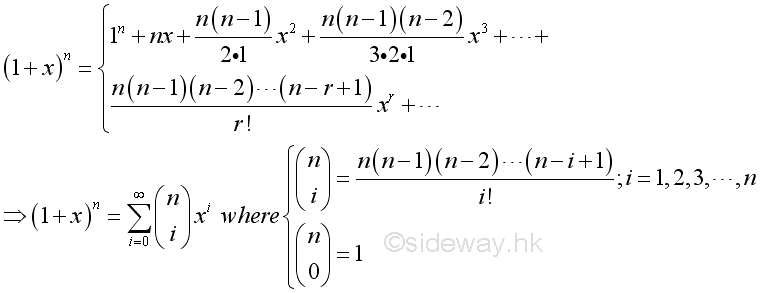
For any number n, if the absolute value of x is less than one, then the series converges absolutely.

If n is a nonnegative integer, the infinite binomial series is reduced to a finite series having the same form of the binomial theorem