Content
Trigonometry
Unit Circle
Circular Functions
The Pythagorean Identity
Reference Angle
Trigonometry
Trigonometry is the study of angles and the angular relationship of triangular figures. Trigonometric functions are important in study triangles and other applications. The two most important trigonometric functions are sine and cosine.
Unit Circle
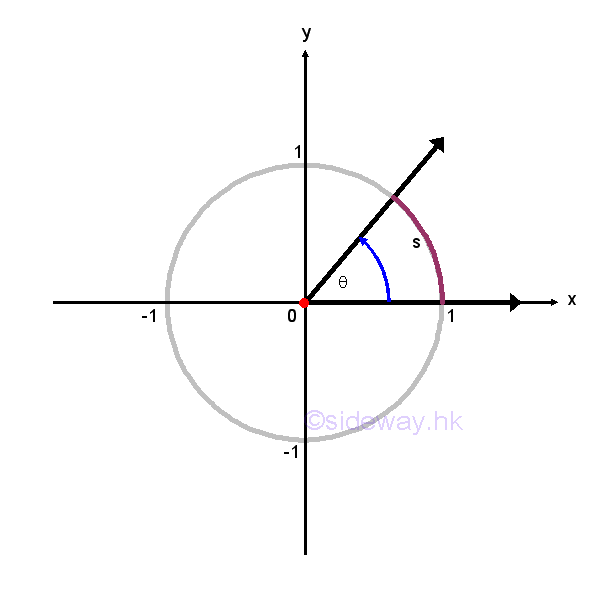
Degree measure is usually used as a decimal measure of an angle, while radian measure is naturally a real number measure of an angle, which is much easier for a continuous angle measurement of an object. Besides, the main advantage of radian measure is the relationship between the angle, θ measure and the are length, s measure. Consider the unit circle, x2+y2=1, on the cartesian coordinate plane, the central subtended angle by the arc in standard position is θ in radian and the corresponding arc is s in lenght. By definition, arc length is equal radius times subtended angle in radian, imply radian θ=s/r=s/1=s.
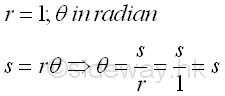
When r=1, the oriented angle can be related to the oriented arc directly. As angle θ in radian equals to arc length s, values of angle θ in radian can be assumed to be lied on the circular real number line wrapped around the unit circle with zero point locating at point (1,0) on the coordinate plane. Since a counter-clockwise angle is positive, a positive angle of t radian is equal to wrap the real number line above x-axis with interval [0,t] counter-clockwise around the unit circle. And since a clockwise angle is negative, a negative angle of -t radian is equal to wrap the real number line below x-axis with interval [-t,0] clockwise around the unit circle. Imply
Circular Functions
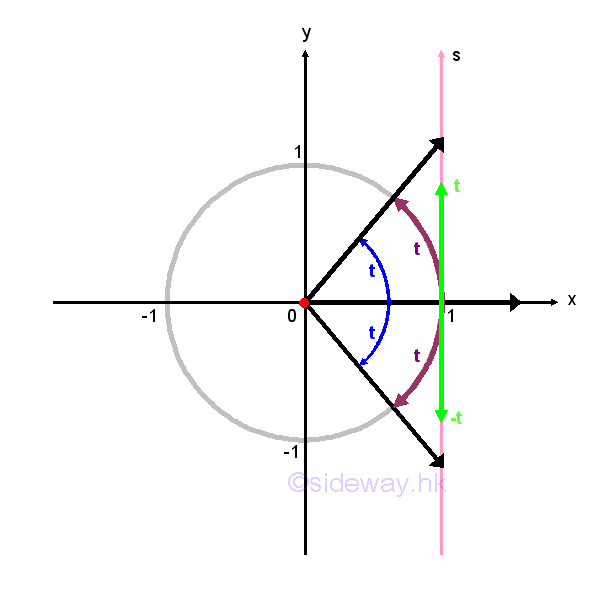
Trigonometric functions are also called circular functions or periodic functions. Although trigonometric functions are defined by the lengths of the sides of a triangle, trigonometric functions can also be defined by making use of the unit circle. For the sine and cosine functions, values of the sine and cosine functions can be determined by the intersection pont of the terminal side of an angle in the standard position with the unit circle on the cartesian coordinate system in a circular way. Imply
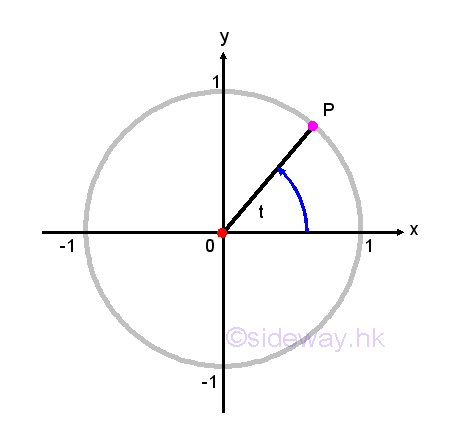
A position of the point P on the unit circle can therefore be assigned to each angle θ in the standard position continuously. By considering the coordinate (x,y) of the point P of intersection associated with the angle θ as the length of the legs of an imaginary right-angled triangle with the length of hypotenuse equal to radius 1. The x-coordinate of P with same definition of cosine is equal to cos(θ), while the y-coordinate of P with same definiton of sine is equal to sin(θ). In other words, there is only one associated value of cos(θ) and only one associated value of sin(θ) for each angle θ. Imply
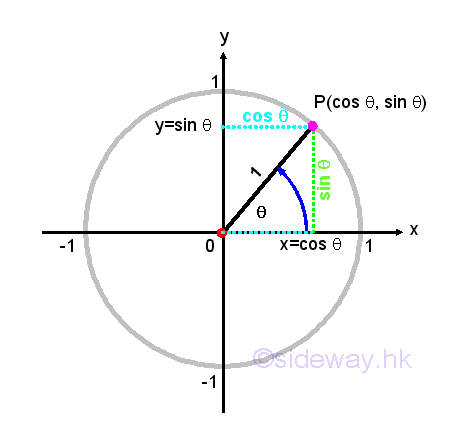
The Pythagorean Identity
As the point P, lied on the unit circle, can be viewed as the leg of a right-angled triangle with hypotenuse equal to 1, the pythagorean theroem can be applied, that is x2+y2=z2. Substituting x=cos(θ), y=sin(θ) and z=1 into the equation x2+y2=1. Imply (cos(θ))2+(sin(θ))2=1 and for convenience the identity is written as cos2(θ)+sin2(θ)=1. The identity implies the theorem is always true for any angle θ. Impy
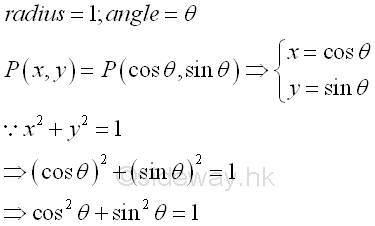
The identity can be used to determine the unknown term up to a sign, ±, when either the cos(θ) or sin(θ) is known. The ambiguity of the sign, ±, can be removed if the terminal side of angle θ lies on the coordinate system in standard position is known. Impy

The Pythagorean theorem can also be applied to a general case for circles of radius r centered at the origin. Let the intersection of the terminal side of angle θ on the unit circle with radius 1 be P(x',y'). Let the new intersection the terminal side of angle θ on the circle with radius r be Q(x,y). Then two similar right-angled triangles ΔOPx' and ΔOQx are formed. And the dimension of the new intersection point Q can be determined by proportional ratio. That is x/x'=r/1=r⇒x=rx' and y/y'=r/1=r⇒y=ry'. The coordinate of new intersection point Q can then be obtained from the intersection point P, that is x=rcos θ, y=rsin θ. Impy
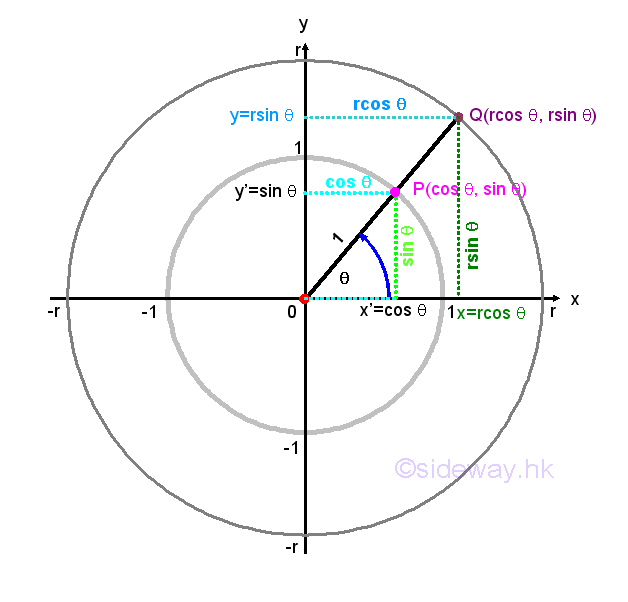
From the pythagorean theorem, x2+y2=r2, then r=√(x2+y2). Since x=rcos θ, y=rsin θ, subsitute into the pythagorean theorem and get, (rcos θ)2+(rsin θ)2=r2 ⇒cos2θ+sin2θ=1 as the Pythagorean identity before. Besides the triangular functions, cosine and sine functions can also determined by the coordinate of the point Q. That is cos θ=x/r=x/√(x2+y2) and sin θ=y/r=y/√(x2+y2). Imply

In general, for an acute angle θ in the standard position on the cartesian coordinate system can always be assumed residing in a right-angled triangle. Let the coordinate of a point on the terminal side of the angle be P(a,b). Then the length of the side adjacent to the angle θ is a and the length of the side opposite to angle θ is b. According to the Pythagorean Theorem, a2+b2=c2, imply the length of the hypotenuse side is c. Imply
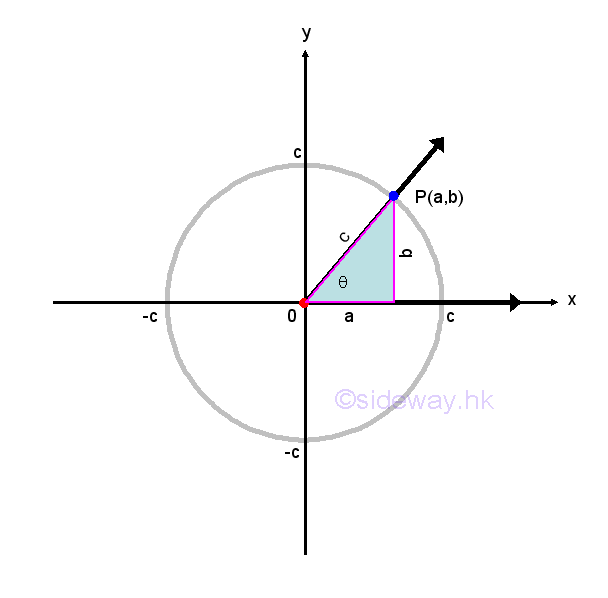
According to the right-angled trigonometry, the sine function sin θ=opposite/hypotebyse=b/c and the cosine function cos θ=adjacent/hypotebyse=a/c. Imply

Reference Angle
Another symmetric property of unit circle in the cartesian coordinate system can also help to determine cosines and sines of angles. Regardless, the values of angle θ, any point P(x,y) lies on the terminal side of angle θ and on the unit circle can have another point Q lying on the unit circle by reflecting the original point P about the x-axis, y-axis or origin. For a non-quadrantal angle θ, the acute angle α made between the termianl side of the angle θ and the x-axis is called the reference angle for θ. Therefore, if angle θ is a quadrant I or IV angle, then angle α is the angle between the terminal side of angle θ and the positive side of x-axis. If angle θ is a quadrant II or III angle, then angle α is the angle between the terminal side of angle θ and the negative side of x-axis. Let angle α be the reference angle for angle θ. Then cos θ=±cos α and sin θ=±sin α and the plus or minus sign depends on the quadrant location of the terminal side of angle θ lies on. In other words, valus of cosine and sine functions for angles on quadrant II, III, and IV can be determined by the corresponding reference angle on quadrant I. Imply
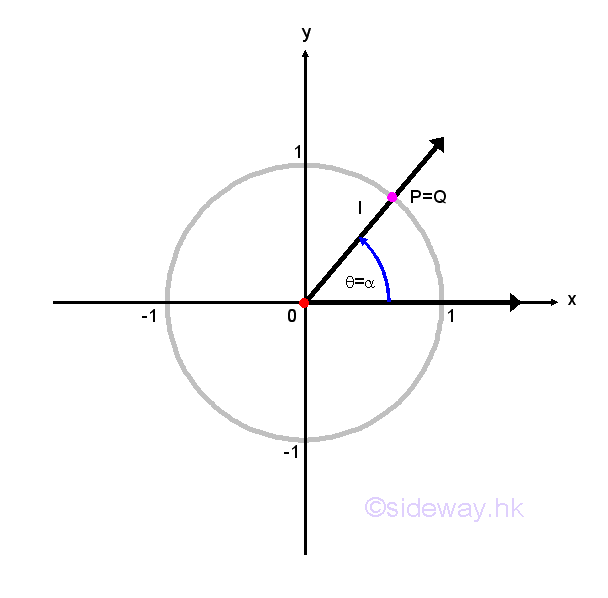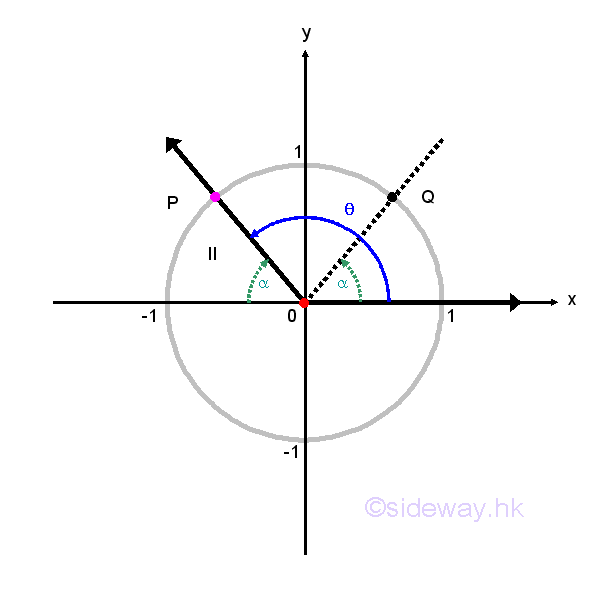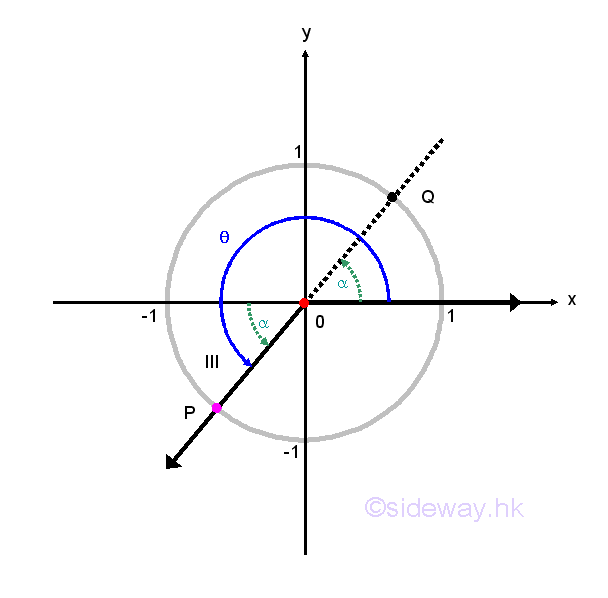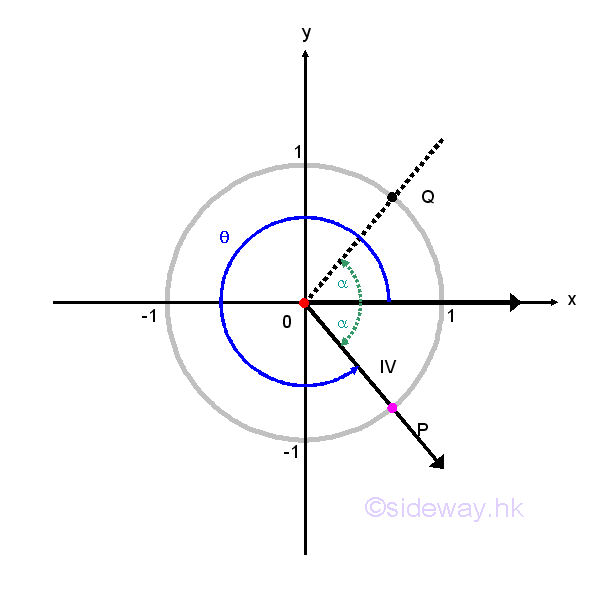
Based on the reference angle theorem, coordinates of common points on the unit circle can be plotted from the known angle of 0, π/6, π/4, π/3, and π/2. Imply
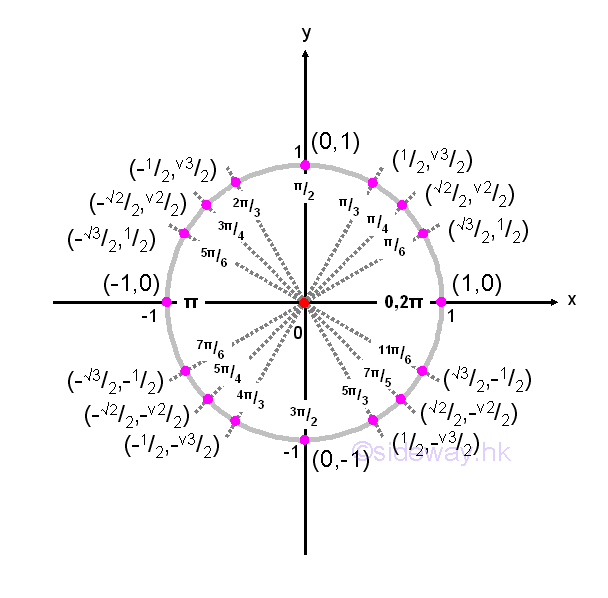
©sideway
ID: 130500026 Last Updated: 5/28/2013 Revision: 1 Ref:
References
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
- Ayres, F. JR, Moyer, R.E., 1999, Schaum's Outlines: Trigonometry
- Hopkings, W., 1833, Elements of Trigonometry
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
