Content

Trigonometry

Although trigonometry is based on the right angled triangle by studying the angle and the angular relationship of triangular figures, trigonometric functions are also called circular functions because trigonometric functions are closely related with the unit circle.

Periodic Functions

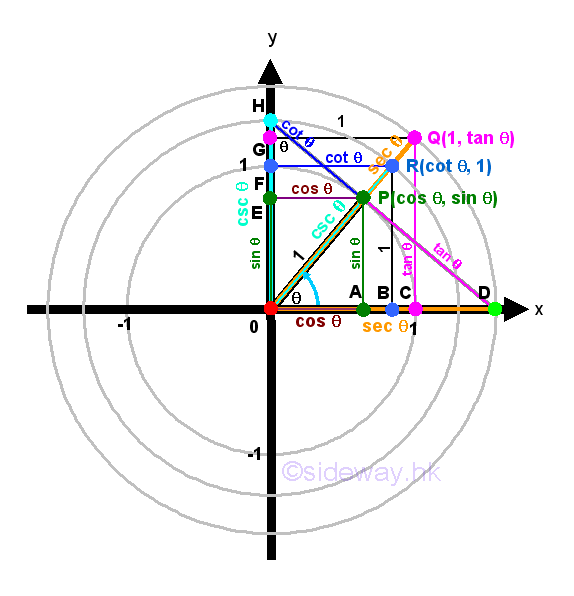
Trigonometric functions are called circular functions or periodic functions because the angles of a trigonometric function can only be varied in a circular way around a circle and the value of the trigonometric functions are function of period 2π. Based on the trigonometric definition of trigonometric functions, trigonometric functions can also be derived or defined using the unit circle concept. All trigonometric functions can then be plotted on the unit circle diagram for easier visualizing the properties of trigometric functions and the relationship between trigometric functions.

Similar and Congruent Triangles

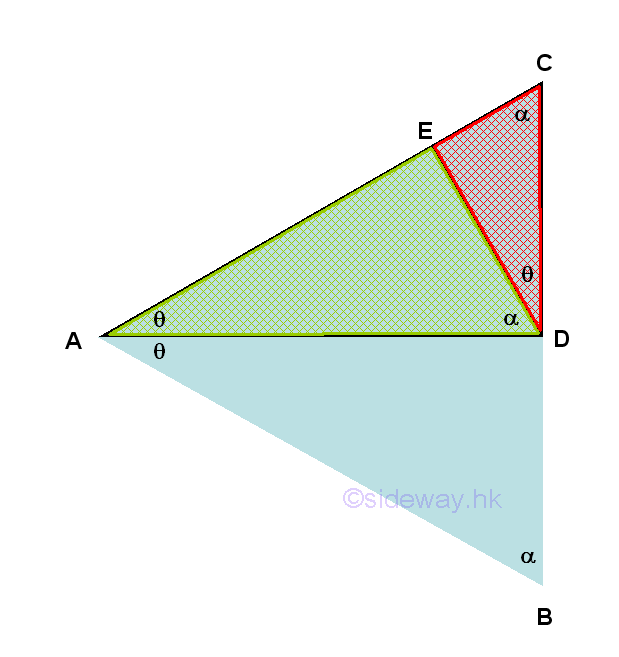
In general, two figures are similar to each other when two figures have the same shape but not necessarily the same size. Scaling a figure by a factor is usually the most common idea to get two similar figures similar to each other. Two triangles are similar when there is a correspondence between the corresponding angles at the vertices of two triangles are congruent or the lengths of the corresponding paired sides of two triangles have the same ratio. These two properties of similar triangles are coexistence because each of these conditions implies the other. Besides, since the sum of the internal angles of a triangle is always equal to 2π, therefore when two of the cooresponding angles are congruent, the third pair of corresponding angle should always be equal also. Based on these properties, besides the AAA Similarity that the three sets of the corresponding paired angles of two triangles are equal, the similarity of two triangles can be determined by either the SSS Similarity that the three sets of the lengths of the corresponding paired sides of two triangles are in proportion of the same ratio or the SAS Similarity that one set of the corresponding paired angle of two triangles is congruent to each other and two sets of the lengths of the corresponding paried sides of two triangles including these angles are in proportion of the same ratio. Therefore by SAS similarity, triangles ΔDAE, ΔCAE and ΔBAD are similar triangles.

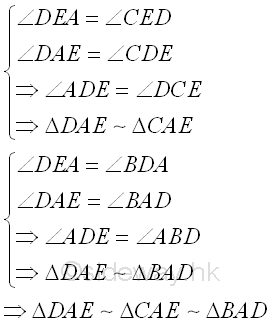
Besides, two figures are congruent to each other when two figures have the same shape and the same sides by maping one figure to anther figure through translation, reflection or rotation or some combination of these transformations without scaling. Two triangles are congruent when there is a correspondence between the corresponding paired sides of two triangles have the same length, while the corresponding angles at the vertices of two triangles are congruent does not guaranty that two triangles are congruent. Based on these properties, besides the SSS condition that the three sets of the corresponding paired sides of two triangles are equal in length, the congruent of two triangles can be determined by the SAS condition that  that one set of the corresponding paired angle of two triangles is congruent to each other and two sets of the lengths of the corresponding paried sides of two triangles including this angle are equal in length. Or the ASA condition that one set of the lengths of the corresponding paried sides of two triangles are equal in length and two sets of the corresponding paired angle of two triangles including these sides is congruent to each other. Or the AAS condition that one set of the lengths of the corresponding paried sides of two triangles are equal in length and two sets of the corresponding paired angle of two triangles that does not includes these sides is congruent to each other.  Or the RHS condition that  one set of the corresponding paired angle of two triangles is congruent to each other, one set of the lengths of the corresponding paried hypotenuse of two triangles are equal in length and one set of the lengths of the corresponding paried other sides of two triangles are equal in length. Therefore by RHS condition, ΔCAD and ΔBAD are congruent triangles. And so ΔCAD is also similar to ΔCD ΔBAD, ΔDAE, and ΔCAE.

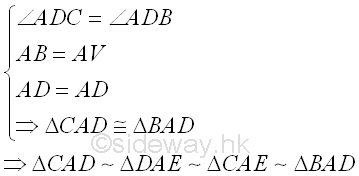
Sine Function

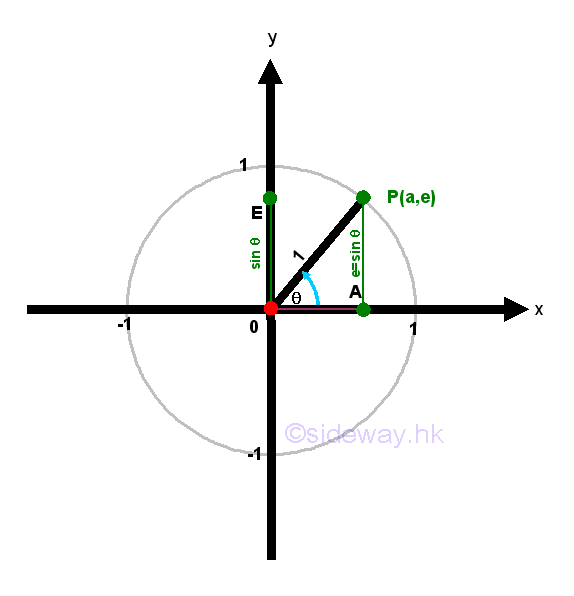
Sine function is a trigonometric function of an angle based on the right angled triangle definition of the ratio of the length of the side opposite to that angle to the length of the hypotenuse of the right angled triangle. By the similarity of triangles, sine function can also be defined using the unit circle approach. Let point P be the intersection between the terminal side of angle θ and the unit circle. Let point A be the vertical projection of point P on x-axis. Let point E be the vertical projection of point P on y-axis. Then the coordinate of point P is P(a,e). Therefore points P, O, and A form a right-angled triangle ΔPOA including angle θ. According to the right angled triangle definition of sine function, sin θ=AP/OP=e/1⇒e=sin θ.

Cosine Function

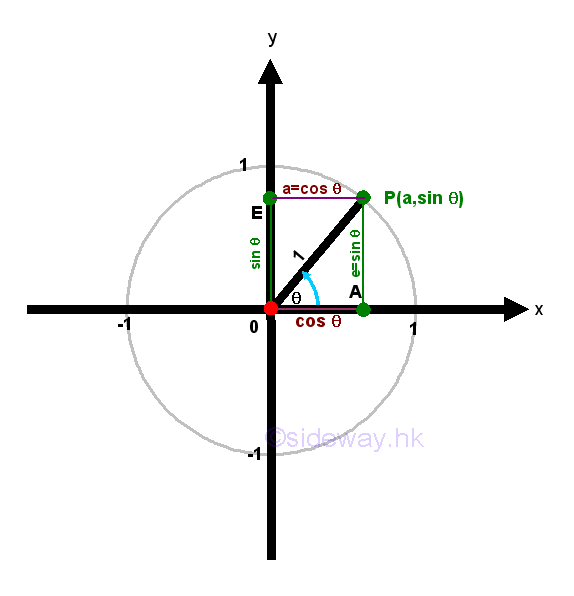
Cosine function is a trigonometric function of an angle based on the right angled triangle definition of the ratio of the length of the side adjacent to that angle to the length of the hypotenuse of the right angled triangle. By the similarity of triangles, cosine function can also be defined using the unit circle approach. Let point P be the intersection between the terminal side of angle θ and the unit circle. Let point A be the vertical projection of point P on x-axis. Let point E be the vertical projection of point P on y-axis. Then the coordinate of point P is P(a,e). Therefore points P, O, and A form a right-angled triangle ΔPOA including angle θ. According to the right angled triangle definition of cosine function, cos θ=OA/OP=a/1⇒a=cos θ.

Tangent Function

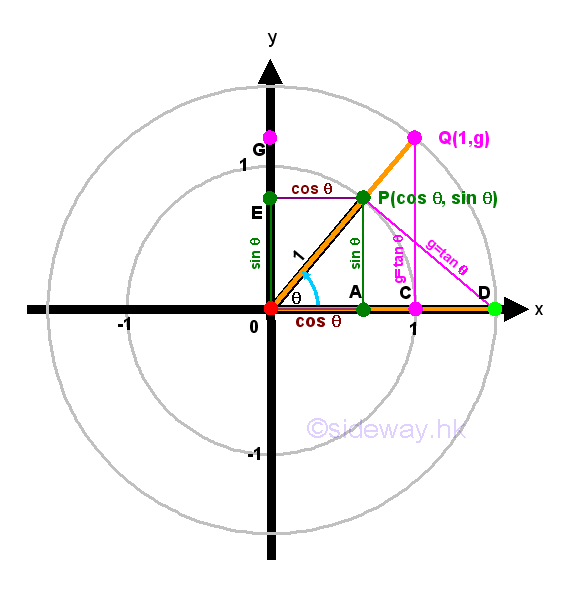
Tangent function is a trigonometric function of an angle based on the right angled triangle definition of the ratio of the length of the side opposite to that angle to the length of the side adjacent to that angle of the right angled triangle. By the similarity of triangles, tangent function can also be defined using the unit circle approach. Let point P be the intersection between the terminal side of angle θ and the unit circle. Let point A be the vertical projection of point P on x-axis. Let point E be the vertical projection of point P on y-axis. Then the coordinate of point P is P(a,e). Therefore points P, O, and A form a right-angled triangle ΔPOA including angle θ. According to the right angled triangle definition of tangent function, tan θ=AP/OA=e/a⇒e/a=tan θ. The expression, e/a only expresses the tangent function in form of a ratio.

There are two ways to derive the value of tangent function by constructing right-angled triangle using unit circle approach. First method, let coordinate of point C be C(1,0) on the x-axis. Construct a vertical line at x=1 from C.  Extend line OP to OQ such that point Q is the intersection of line OQ and CQ. Therefore points Q, O, and C form a right-angled triangle ΔQOC including angle θ. By SAS similarity, ΔQOC is similar to ΔPOA. Imply lengths of the corresponding paired sides of two triangles have the same ratio. That is CQ/AP=OC/OA. Imply g/e=1/a⇒g=e/a=tan θ.

Second method, construct a line from point P and perpendicular to the line OP to the x-axis. Let point D be the point of intersection between the line OD and the x axis. Therefore points D, O, and P form a right-angled triangle ΔDOP including angle θ. By ASA condition, ΔDOP and ΔQOC are congruent triangles. That is OP=OC and PD=CQ. Imply PD/OP=CQ/OC⇒PD/1=g/1⇒PD=g=tan θ.

Cotangent Function

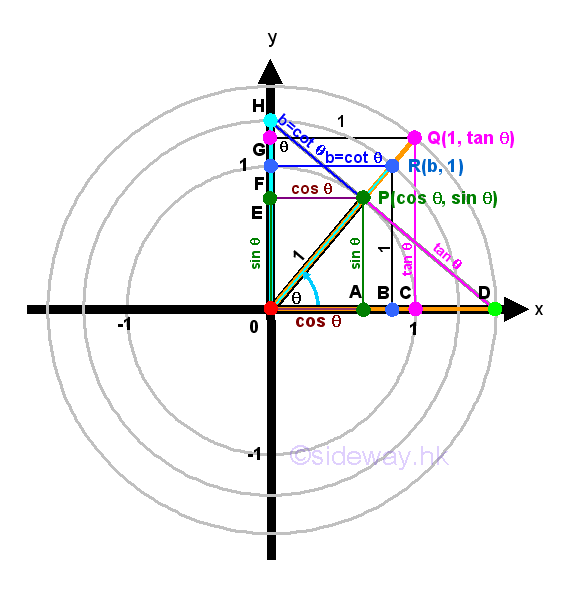
Cotangent function is a trigonometric function of an angle based on the right angled triangle definition of the ratio of the length of the side adjacent to that angle to the length of the side opposite to that angle of the right angled triangle, that is the reciprocal of tangent function. By the similarity of triangles, cotangent function can also be defined using the unit circle approach. Let point P be the intersection between the terminal side of angle θ and the unit circle. Let point A be the vertical projection of point P on x-axis. Let point E be the vertical projection of point P on y-axis. Then the coordinate of point P is P(a,e). Therefore points P, O, and A form a right-angled triangle ΔPOA including angle θ. According to the right angled triangle definition of cotangent function, cot θ=OA/AP=a/e⇒a/e=cot θ. The expression, a/e only expresses the cotangent function in form of a ratio.

There are two ways to derive the value of cotangent function by constructing right-angled triangle using unit circle approach. First method, let coordinate of point F be F(0,1) on the y-axis. Construct a horizontal line at y=1 from F.  Extend line OP to OR such that point R is the intersection of line OR and FR. Then construct another vertical line from R to x-axis such that point B is the intersection of the line RB and x-axis. Therefore points R, O, and B form a right-angled triangle ΔROB including angle θ. By SAS similarity, ΔROB is similar to ΔPOA. Imply lengths of the corresponding paired sides of two triangles have the same ratio. That is BR/AP=OB/OA. Imply 1/e=b/a⇒b=a/e=1/tan θ=cot θ.

Second method, construct a line from point P and perpendicular to the line OP to the y-axis. Let point H be the point of intersection between the line OH and the y axis. Therefore points H, O, and P form a right-angled triangle ΔHOP including angle θ. By ASA condition, ΔOHP and ΔROB are congruent triangles. That is PO=BR and HP=OB. Imply HP/PO=OB/BR⇒HP/1=b/1⇒HP=b=cot θ.

Secant Function

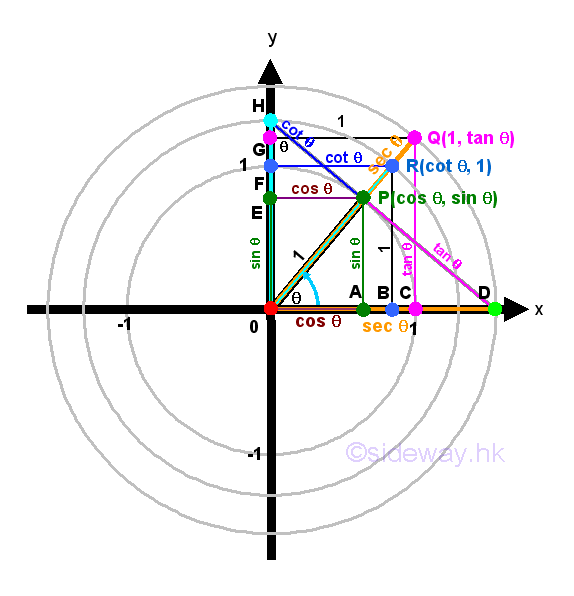
Secant function is a trigonometric function of an angle based on the right angled triangle definition of the ratio of  the length of the  hypotenuse of the right angled triangle to the length of the side adjacent to that angle, that is the reciprocal of cosine function. By the similarity of triangles, secant function can also be defined using the unit circle approach. Let point P be the intersection between the terminal side of angle θ and the unit circle. Let point A be the vertical projection of point P on x-axis. Let point E be the vertical projection of point P on y-axis. Then the coordinate of point P is P(a,e). Therefore points P, O, and A form a right-angled triangle ΔPOA including angle θ. According to the right angled triangle definition of secant function, sec θ=OP/OA=1/a⇒1/a=1/cos θ=sec θ. The expression, 1/a only expresses the secant function in form of a ratio.

There are two ways to derive the value of secant function by constructing right-angled triangle using unit circle approach as in deriving the tangent function. First method, let coordinate of point C be C(1,0) on the x-axis. Construct a vertical line at x=1 from C.  Extend line OP to OQ such that point Q is the intersection of line OQ and CQ. Therefore points Q, O, and C form a right-angled triangle ΔQOC including angle θ. By SAS similarity, ΔQOC is similar to ΔPOA. Imply lengths of the corresponding paired sides of two triangles have the same ratio. That is OC/OA=OQ/OP. Imply 1/a=OQ/1⇒OQ=√(1+g2)=1/a=1/cos θ=sec θ.

Second method, construct a line from point P and perpendicular to the line OP to the x-axis. Let point D be the point of intersection between the line OD and the x axis. Therefore points D, O, and P form a right-angled triangle ΔDOP including angle θ. By ASA condition, ΔDOP and ΔQOC are congruent triangles. That is OP=OC and OD=OQ. Imply OD/OP=OQ/OC⇒OD/1=OQ/1⇒OD=OQ=√(1+g2)=sec θ.

Cosecant Function

Cosecant function is a trigonometric function of an angle based on the right angled triangle definition of the ratio of  the length of the  hypotenuse of the right angled triangle to the length of the side opposite to that angle, that is the reciprocal of sine function. By the similarity of triangles, cosecant function can also be defined using the unit circle approach. Let point P be the intersection between the terminal side of angle θ and the unit circle. Let point A be the vertical projection of point P on x-axis. Let point E be the vertical projection of point P on y-axis. Then the coordinate of point P is P(a,e). Therefore points P, O, and A form a right-angled triangle ΔPOA including angle θ. According to the right angled triangle definition of cosecant function, csc θ=OP/AP=1/e⇒1/e=1/sin θ=csc θ. The expression, 1/e only expresses the cosecant function in form of a ratio.

There are two ways to derive the value of cotangent function by constructing right-angled triangle using unit circle approach. First method, let coordinate of point F be F(0,1) on the y-axis. Construct a horizontal line at y=1 from F.  Extend line OP to OR such that point R is the intersection of line OR and FR. Then construct another vertical line from R to x-axis such that point B is the intersection of the line RB and x-axis. Therefore points R, O, and B form a right-angled triangle ΔROB including angle θ. By SAS similarity, ΔROB is similar to ΔPOA. Imply lengths of the corresponding paired sides of two triangles have the same ratio. That is OR/OP=BR/AP. Imply OR/1=1/e⇒OR=√(1+b2)=1/e=1/sin θ=csc θ.

Second method, construct a line from point P and perpendicular to the line OP to the y-axis. Let point H be the point of intersection between the line OH and the y axis. Therefore points H, O, and P form a right-angled triangle ΔHOP including angle θ. By ASA condition, ΔOHP and ΔROB are congruent triangles. That is PO=BR and HO=OR. Imply HO/PO=OR/BR⇒HO/1=OR/1⇒HO=OR=√(1+b2)=csc θ.