Vectors

In practical applications, many quantities can be descibed by a magnitude completely in the form of size or number of units according to a scale. For examples, mass of a body, volume of a body, etc. These kinds of quantities are called scalars, or scalar quantites. However, there are also many quantities that cannot be descibed by only one single number completely. For example, force of an applied load, velocity of a body. These kinds of quantities require another characteristic specification, a direction to specify the way to act, in order to complete the description of a quantity. In general, these kinds of quantities can be represeneted graphically by directed line segment, arrow, with which the direction is indicated by the arrow cue pointing and the magnitude is represented by the total length of the arrow. As quantities characterized by both direction and magnitude can be represented by a directed line segment, these kinds of quantities are called vectors, or vector quantities.

Definition of Vector QuantityA vector quantity is the mathematical representation of a physical entity that is characterized by magnitude and direction.

Vector Notation

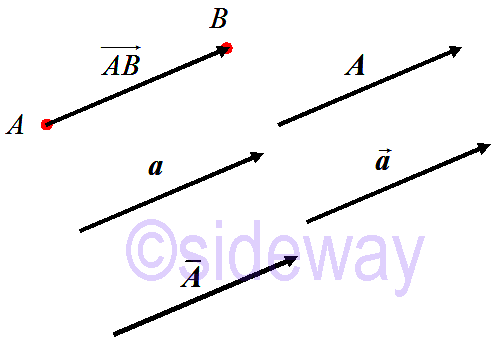Mathematically, a vector is usually denoted by a bold letter, e.g. 𝒂, 𝑨, or with overbar, e.g. 𝑨, or with over arrow, e.g. 𝑨, or initial point, 𝐴 and final point, 𝐵 with over arrow 𝐴𝐵. And the length of a vector is usually denoted by the absolute value symbol e.g. |𝒂|.

Concept of Vector

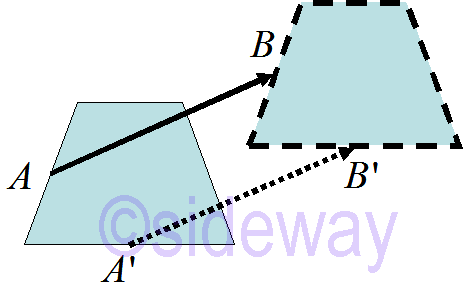One practical application example is the translation of a body. The translation motion of the body is charactered by both the linear displacement and the direction of the movement. Similarly the translation can be graphically represented by a directed line segment linking the original reference position of a point on the body as the initial point 𝐴 and the final reference position of the same point on the body after translation as the terminal point 𝐵. Since the motion of each point on the body is the same, a group of directed line segments of the same length and same direction can be constructed for every point of the body. Therefore graphically a vector, 𝐴𝐵 is a directed line segment used to represent the specified quantity with the length of the directed line segment is equal to the length of the vector and the direction of the directed line segment is equal to the direction of the vector. Since two equal directed line segments imply two equal quantities, two vector quantities are equal if and only if both vectors have the same length and the same direction. the directed arrow is also called the sense of the vector. The length of a vector is also called the magnitude or the Euclidean norm of the vector. The basic definition of a vector can therefore be expressed as following.

Basic Concept of Vector Bound Vctor : In a rectangular Cartesian coordinate system, a bound vector, 𝐴𝐵, is an arrow bounded to an initial point 𝐴 in space. The arrow is a directed line segment displaced from an initial point, 𝐴, to a terminal point 𝐵. A free displacement vector 𝒄 can be determined by the linear displacement from initial point 𝐴 to terminal point 𝐵. That is, 𝒄 is equal to 𝐴𝐵 in magnetude and direction but 𝒄 is not bounded to initial point 𝐴.

             Position Vector : Using similar concept, two position vectors, 𝑂𝐴 and 𝑂𝐵 can be constructed from point 𝐴 and point 𝐵 by bounding them to the origin point 𝑂 to indicate the position of points in space respectively.

             Free Vector :  Since the coordinates of origin 𝑂 are equal to 0, position vectors, 𝑂𝐴 and 𝑂𝐵 are naturally free vectors usually named 𝒂 and 𝒃, and all are equal to their coordinates accordingly.
             Therefore vector 𝒄=𝐴𝐵 can be expressed in terms of free vectors 𝒂 and 𝒃 and is equal to final position minus initial position. That is 𝒄=𝐴𝐵=𝑂𝐵−𝑂𝐴=𝒃−𝒂.

Kinds of Vectors

In practical applications, there are two kinds of vectors, free vector and bound vector.

Free Vector

A free vector is only used to specify the magnitude and direction with reference to a coordinate system of a physical entity. And this is the most general case. For example, a force vector is a free vector used to specify the magnitude and direction with reference to a coordinate system of the line of action through the point of action that the applied force is applied.

Bound Vector

A bound or anchored vector, is used to specify both the magnitude and direction with reference to a coordinate system of a physical entity at a specific location. For example, a displacement vector is a bound vector used to specify the displacement magnitude and direction with reference to a coordinate system of a specific location to another location. Or a wind field vector is an anchored vector used to specify wind velocity, magnitude and direction with reference to a coordinate system at a specific location of interest in space.

Types of Vectors

Some typical vectors are

Zero Vector

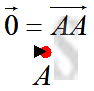A zero vector, or a null vector, is a vector with magnitude equal to zero. Since the magnitude of the vector is zero, the initial point of the vector coincides with the terminal point, i.e. 𝐴𝐴. In other words, the direction of a zero vertor is indeterminate. The zero vector is usually denoted as 𝟎.

Unit Vector

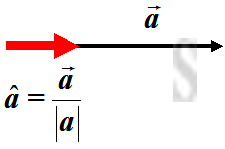A unit vector is a vector with magnitude equal to 1 unit or unity. The unit vector in the direction of a given vector 𝒂 is usually denoted as 𝒂. And the relationship between two vectors is 𝒂=~~𝒂|𝒂|~~. Although all unit vectors have the same magnitude, but the direction of two unit vectors may be in different direction, therefore two unit vectors can not always be considered as equal unless two unit vector have the same direction also.

Position Vector

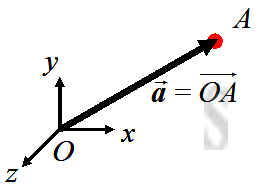A position vector is used to specify the position of a point with respect to the origin reference point. If point 𝑂 is the origin reference of a system and point 𝐴 is the point of interest, then a position vector 𝒂 can be constructed by drawing a vector, 𝑂𝐴, from point 𝑂 to point 𝐴, that is 𝒂=𝑂𝐴.

Displacement Vector

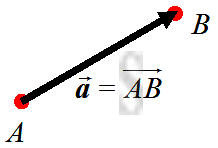A displacement vector is used to specify the magnitude and direction of a displacement with respect to any given reference point to a destination point. Therefore a displacement vector, e.g. 𝐴𝐵, can also be used to denote a displacement from an initial point, 𝐴 to a final point, 𝐵.

Negative Vector

A negative vector is used to specify a vector that is of the same magnetude but in opposite direction of a given vector. That is 𝐵𝐴=−𝐴𝐵 or 𝒃=−𝒂.

Equal Vectors

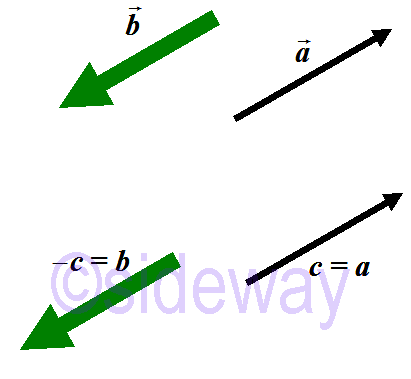Two vectors are said to be equal only when both the magnitude and direction of the two vectors are the same, that is 𝒂=𝒄.

Like Vectors

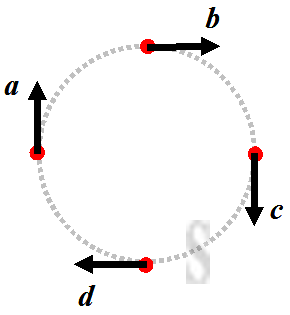
Two or more vectors are called like vectors if both vectors have the same direction irrespective of their magnitudes. e.g. like vectors 𝒂, 𝒄.

Unlike Vectors

Two vectors are called unlike vectors if both vectors have opposite direction with respect to each other irrespective of their magnitudes. e.g. unlike vectors 𝒃, 𝒅.

Coinitial Vectors

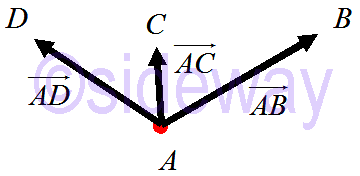Two or more vectors are called coinitial vectors if all vectors have the same initial point irrespective of their magnitudes and direction. For examples 𝐴𝐵, 𝐴𝐶 and 𝐴𝐷 are coinitial vectors.

Collinear Vectors

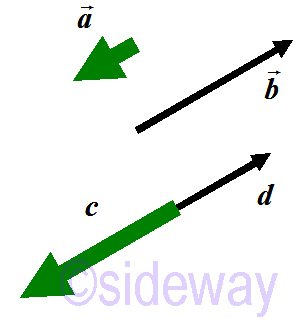Two or more vectors are called collinear vectors, or parallel vectors if all vectors lie along the same line or parallel lines irrespective of their magnitudes and direction. e.g. collinear vectors 𝒂, 𝒃, 𝒄, 𝒅.

Co-planar Vectors

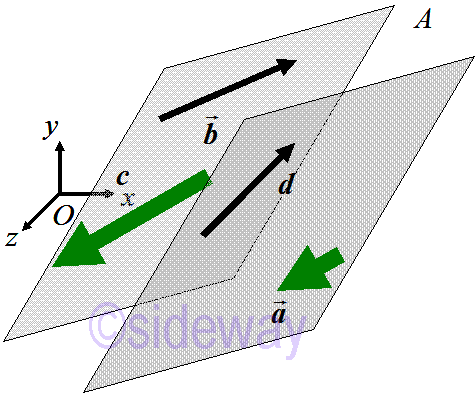Three or more vectors are called coplanar vectors if all vectors lie in the same plane or parallel planes to the same plane irrespective of their magnitudes and direction. e.g. coplanar vectors 𝒂, 𝒃, 𝒄, 𝒅. And two vectors are always coplanar because there is always a plane parallel to any two vectors.