Content
Divisibility
Divisibility Test
Divisibility Test for a Numberr a Number
Divisibility
The divisibility of a positive number by an integer divisor can be determined by some divisibility rule. The divisibility rules are usually a test to test the digits of a number without performing the division directly.
Divisibility Test
A base 10 number, a, can be expressed in terms of digits ai, that is
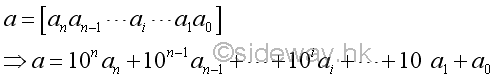
Some standard divisibility tests are as following
-
Testing of Ending Digit Block
A base 10 number can also be expressed as the sum of two parts. If the number a is divided by a divisor, d, the divisor, d, must divides both parts. In other words, for a divisor dividing the power of ten, the divisor divides the given number if and only if the divisor divides the ending digits.
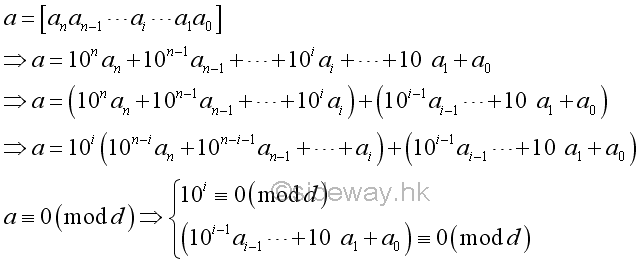
For example,
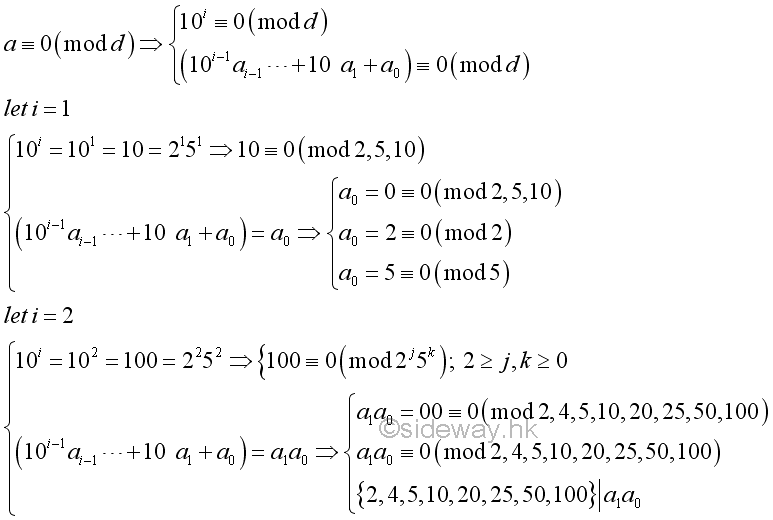
Therefore, this is the divisibility test for numbers by number with prime factor 2 and 5.
-
Testing of the Sum of Digit Blocks
Instead of expressing a base 10 number as the sum of two parts, a base 10 number can also be expressed in forms of parts of fixed size digit blocks. By deducting the sum of digit blocks from the given number, the coefficients of remaining digit blocks become a repeated pattern of digit 9. If the number a is divided by a divisor, d, the divisor, d, must divides the sum of digit blocks and all parts of fixed size digit blocks. In other words, for a divisor dividing the power of ten minus 1, the divisor divides the given number if and only if the divisor divides the sum of digit blocks.

For example,
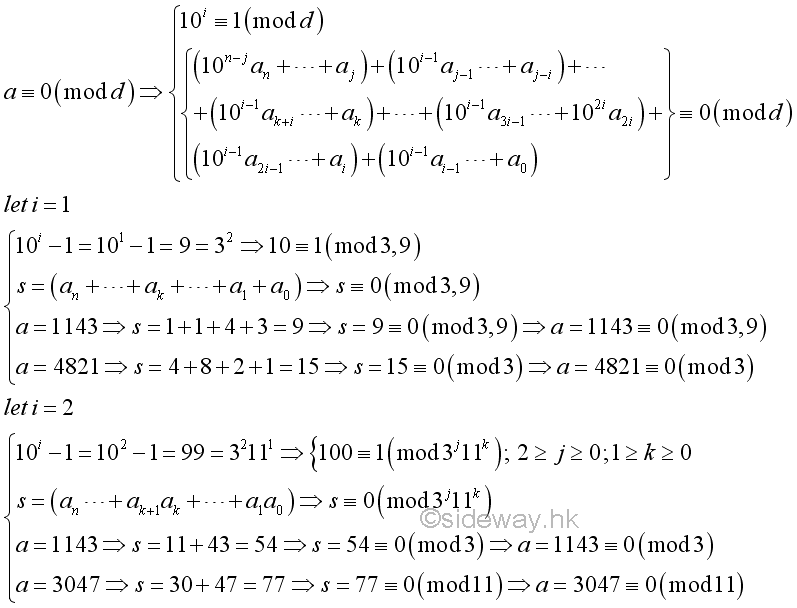
Therefore, this is the divisibility test for numbers by number with prime factor of a digit block with dight 9s, i.e. 9, 99, 999,....
-
Testing of the Alternating Sum of Digit Blocks
Similar to testing of the sum of digit blocks, a base 10 number can be expressed in forms of parts of fixed size digit blocks. Instead of refering to the digit block of "9...9", a digit block of the form "10...01". The relation can be determined by modular arithmetic. By using modular arithmetic, the coefficients of digit blocks become an alternating sum of digit blocks. If a number a is divided by the divisor, d, the divisor, d, must divide the alternating sum of digit blocks also. In other words, for a divisor dividing the power of ten plus 1, the divisor divides the given number if and only if the divisor divides the alternating sum of digit blocks.

The same relation can also be determined algebrically as in testing of the sum of digit blocks. The coefficient of all negative terms are always divided by the first coefficient 10i+1, i.e. 10i+1|10i+2x+1. Besides, The coefficient of all positive terms are also always divided by the first coefficient 10i+1, i.e. 10i+1|10i+2x+1-1.
For example,
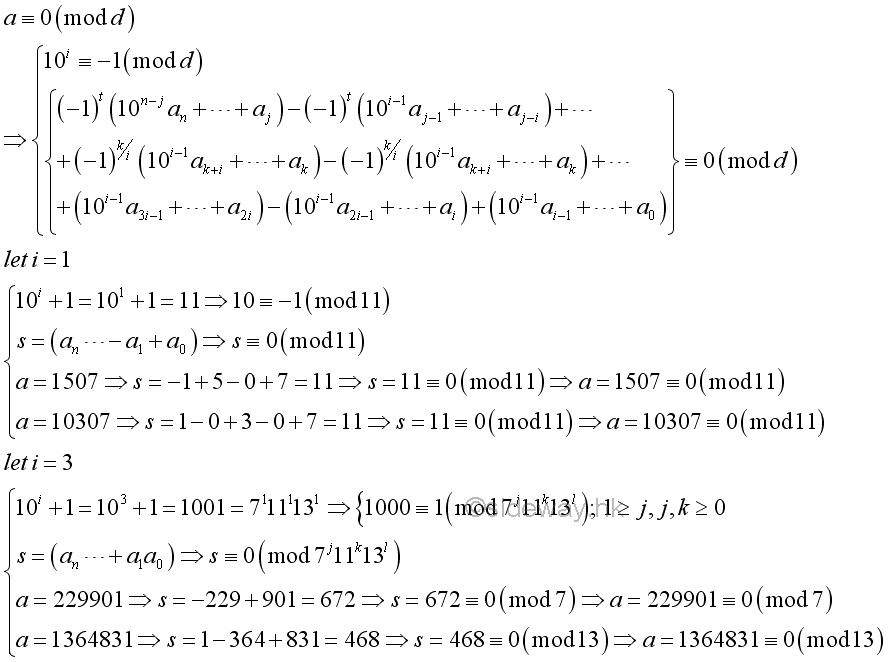
-
Eliminate from the right digit block
Instead of testing the ending digit block, the ending digit block can also be eliminated by reducing the coefficient of the front digit block from the powers of ten to 1 so as to reduce the given number by a digit block from the right.
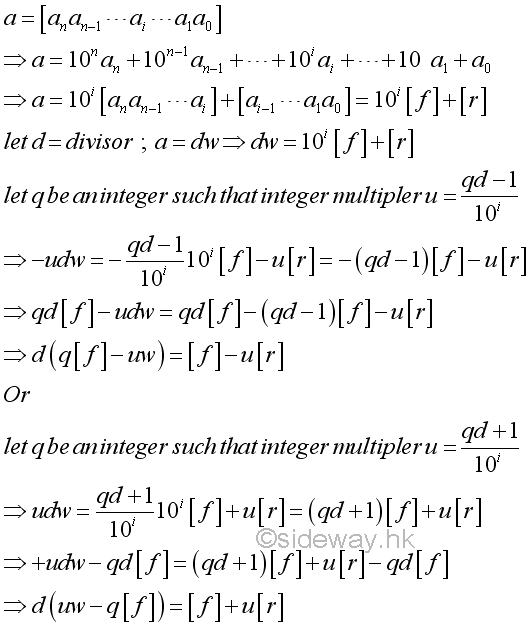
The same relation can also be determined using modular arithmetic. The integer multipler u is expressed as an inverse of 10i modulo d.
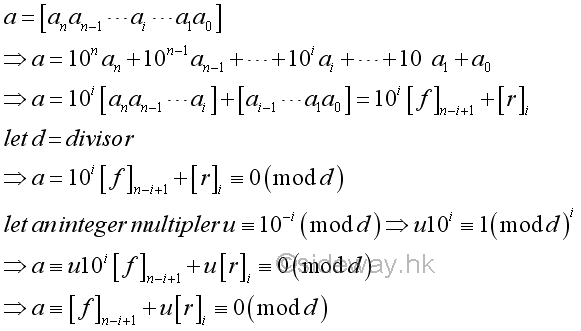
For example,
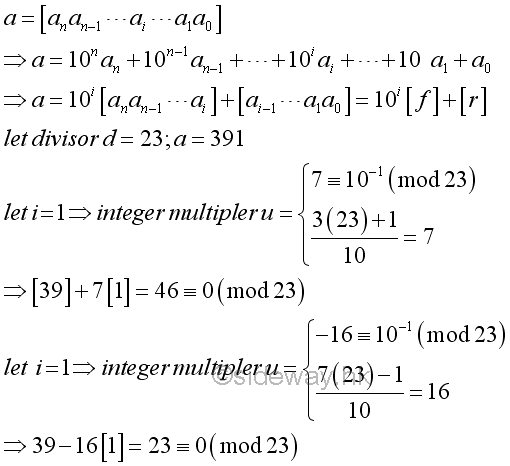
-
Eliminate from the left digit block
Similar to eliminating from the right dight block, the beginning digit block can also be eliminated by reducing the coefficient of the front digit block by powers of ten so as to reduce the given number by a digit block from the left.

The integer multipler u can also be determined algebrically
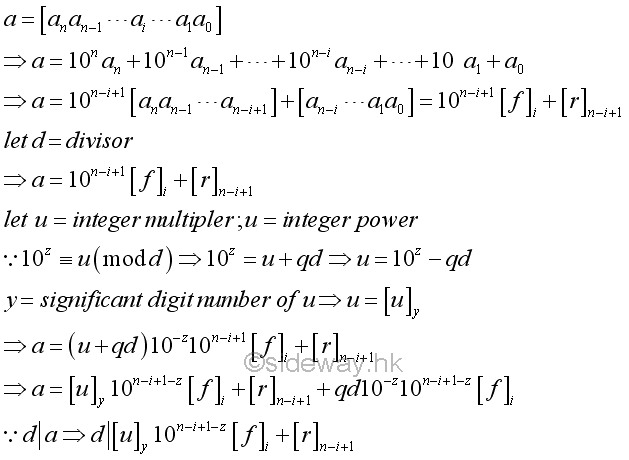
For example,
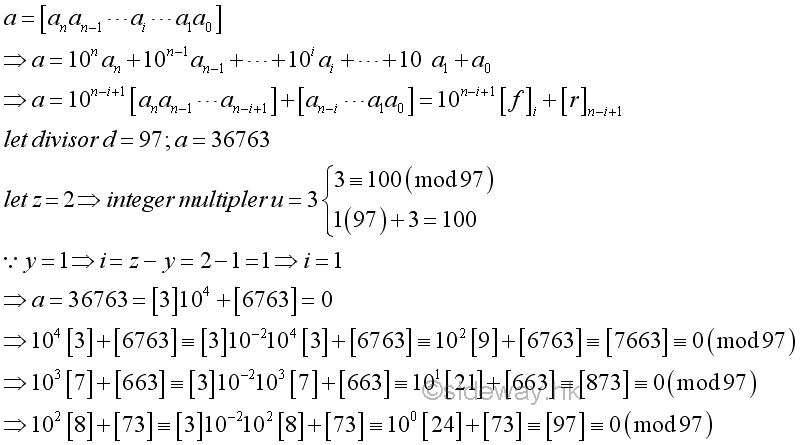
-
Factor the Divisor
For a composite divisor, the divisibility tests for each prime factor of the composite divisor can be used to test the given numebr one by one seperately.
Divisibility Test for a Numberr a Number
The divisibility of an integer number for some integers can be examined by some rules:
-
2 - number with the last digit is even
-
3 - number with the sum of digits is divisible by 3
-
4 - number with the number of the last two digits is divisible by 4
-
5 - number with the last digit is 5 or 0
-
6 - number is divisible by both 2 and 3
-
7 - number with the number without the last digit minus the double of the last digit is equal to 0 or divisible by 7
-
8 - number with the number of the last three digits is divisible by 8
-
9 - number with the sum of digits is divisible by 9
-
10 - number with the last digit is 0
-
11 - number with the sum of every second digit minus the sum of other digits is equal to 0 or divisible by 11
-
12 - number is divisible by both 3 and 4
-
25 - number with the number of the last two digit is 00, 25, 50, or 75
©sideway
ID: 160300002 Last Updated: 3/2/2016 Revision: 0 Ref:
References
- R. Paulo, 1996, The New Book of Prime Number Records
- Wolstenholme, R.J., 1862, On Certain Properties of Prime Numbers
- Mann, H.B., Shanks D., 1972, A Necessary and Sufficient Condition for Primality, and Its Source
- J.M Pollard, Kangaroos, 1975, A Monte Carlo Method for Factorization
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
