Content
Finite Element Analysis
One Dimensional Linear Element: Strain and Stress Approach
One Dimensional Linear Element: Example of a 2 elements system
One Dimensional Linear Element: Energy Approach
Strain Energy
Displacement Function
Total Potential Energy
Principle of Minimum Total Potential Energy
Finite Element Analysis
One dimensional linear element can be used to analysis structural pin jointed problems.
One Dimensional Linear Element: Strain and Stress Approach
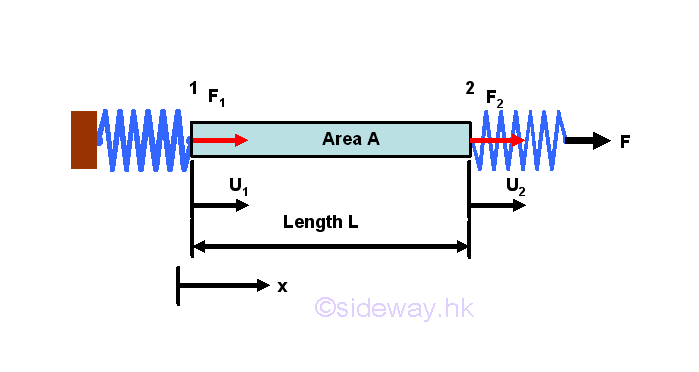
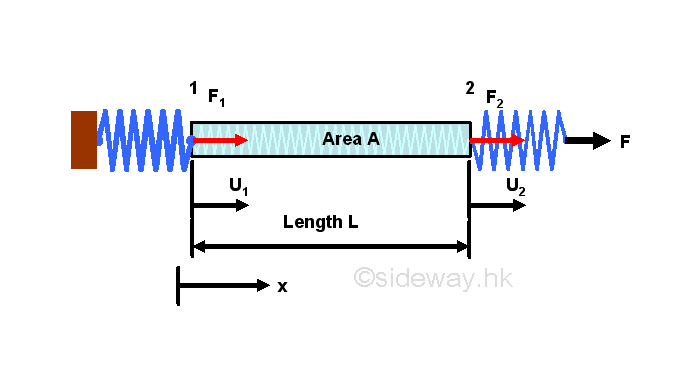
Considering a bar, of length L and cross sectional area A, is subjected to a axial spring loads. Let forces at 1 and 2 are equal to F1 and F2 and the displacements of the bar due to the applied load F is u1 and u2 respectively. Assuming the material of the bar is linear elastic, then the stress-strain relationships of the bar is equal to

Stress is defined as the average force per unit area. That is
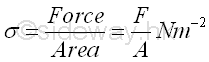
Young's modulus, E or the elastic modulus, is a numerical value to describes the elastic properties of the material undergoing elastic deformation. The unit of Young's modulus is also Nm-2 since strain does not have any unit. Strain is defined as the ratio of total deformation over the original dimension of the bar. That is
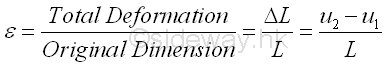
Subsitute equations of stress and strain into the stress-strain relationships of the bar, and a force-deformation relationship expressed in terms of force and displacement is obtained.
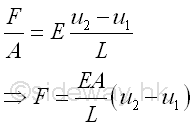
When considering the bar as an individual object, forces, F1 and F2 at both ends of the bar can be expressed analytically as following by assuming a fixed end opposite to the interested force with one consistent coordinate system.
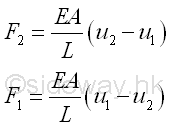
The bar can also considered as an element of the system, in which both forces F1 and F2 and displacement u1 and u2 are expressed as one individual element. This can be done by expressing the two force equations in matrix form as
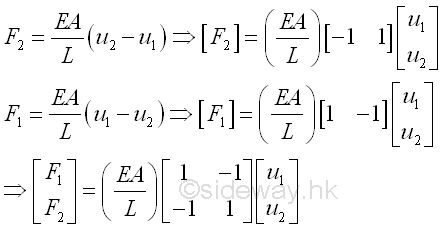
And expressed concisely in an element-wise matrix form which can be used in numerical method as
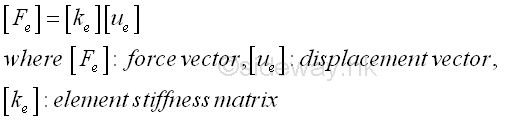
One Dimensional Linear Element: Example of a 2 elements system
Consider a simple system with 2 elements of same material of Young's modulus E, length L and area A. Two elements are connected by a hinge, with one end of element 1 is fixed to a wall, while one end of element 2 is under an applied load F.
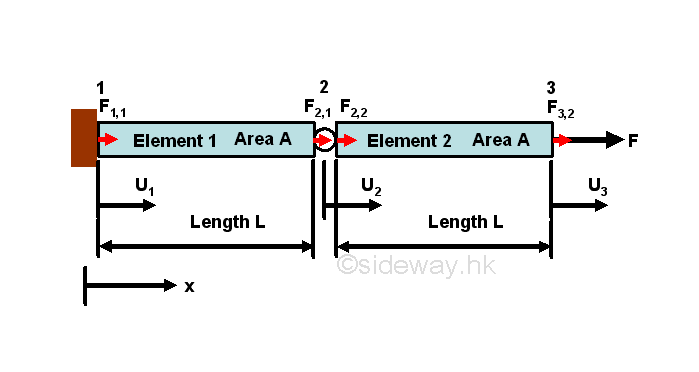
Using the standard coordinate system, the force-displacement equations for elements 1 and 2 are
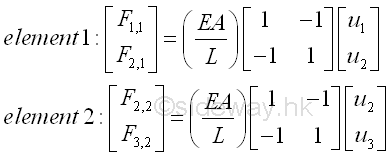
The two force-displacement equations for elements are only elemental equations of the 2 element sytem. Numerically, the force-displacement equations can be combined together to form a bigger system matrix form.
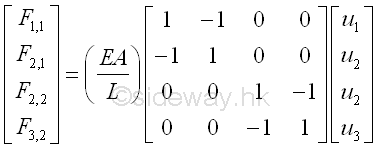
As node 2 is a common point for force F2,1 and F2,2, forces acting on node 2 can further be combined by assembling or grouping the two related force and displacement equations into one equation only. The global matrix form can be reduced to have equations for 3 nodes only.
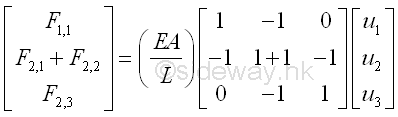
The 3 equations are used to represent the mechanical properties at the 3 nodes. In other words, the magnitudes of force and displacement global element matrix are bounded by the mechanical properties of the physical system. At node 1, the displacement u1 is equal to zero, and the reaction force F1,1 is unknown and is equal to the total reaction force F1 at node 1. At node 2, the displacement u2 is unknown, and the resultant force F2,1+F2,2 is equal to zero since the total reaction force F2 at node 2 is in equilibrium. At node 3, the displacement u3 is unknown, and the resultant force F3,2 is equal to the applied load F, the total reaction force F3 at node 3. That is
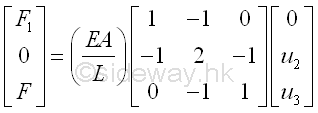
Since there are three force and displacement equations and three unknown, the force and displacement equations can solved.
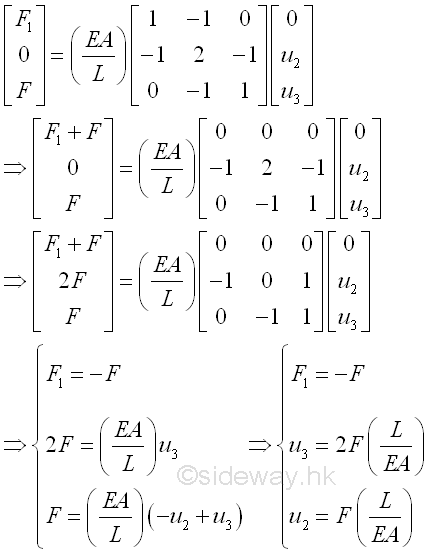
One Dimensional Linear Element: Energy Approach
Strain Energy
The force analytical approach to derive the element stiffness matrix gives an fundamental idea on the numerical method in finite element analysis. An energy approach is an alternative way to derive the element stiffness matrix. The elastic deformation of the bar under applied load reacts like a mechanical spring, strain energy is stored by the system when undergoing deformation. The strain energy, U, per unit volume is equal to
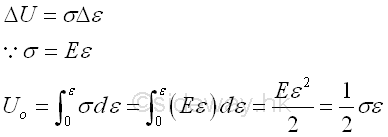
Since displacement is a function of x, local x, along x direction, strain energy for the bar of length L with constant sectional area is equal to
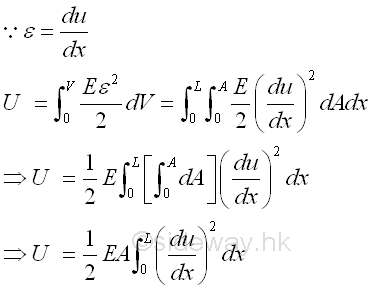
Displacement Function
For a two-node linear element, the linear displacement function can be assumed to be a linear function of x. That is
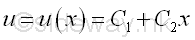
Similar to other boundary problems, this trial displacement function for the bar must satisfy the boundary displacement conditions at two nodes. That is
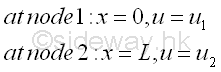
The displacement function is therefore equal to
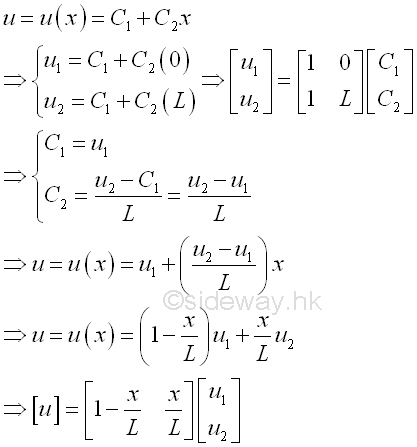
The displacement function can therefore be used to describe the displacement of each particle along the bar. The functions that used to multiply the nodal displacements u1 and u2 are therefore called shape functions or interpolation functions. The differentiation of the displacement function is equal to
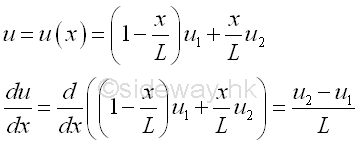
Total Potential Energy
The total strain energy stored in the bar element is therefore equal to
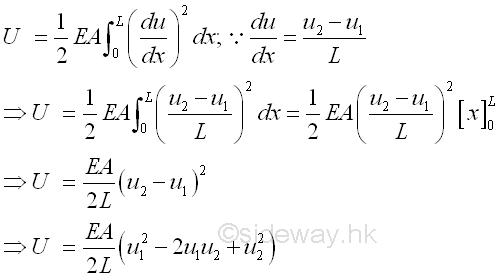
Work done is defined as the applied force times the travelled distance along the direction of the applied force. That is
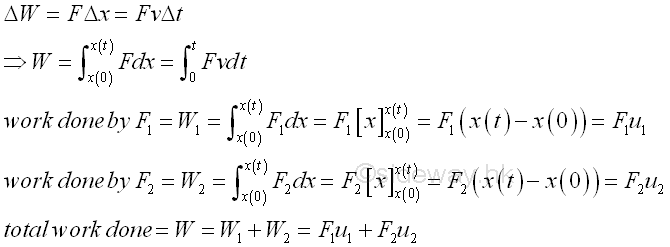
Work potential is defined as the negative of the work done by the external forces acting on the structure. Since the deformed state of the bar element attained upon the application of applied loads is in the equilibrium state, the total potential energy (TPE) or potential energy (PE) of the bar element is defined as the sum of the strain energy (SE) and the work potential (WP). That is
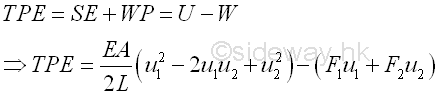
Principle of Minimum Total Potential Energy
The total potential energy (TPE) equation provides a relationship between the applied forces and displacements of element nodes. The deformation due to the applied forces are in static equilibrium. From the principle of minimum total potential energy, a conservative system is in equilibrium if the total potential energy of the system is stationary. The principle implies that the conservative system will only attain a unique deformation at an equilibrium point to achieve the equilibrium state with respect to the independent variables for the given forces. The unique deformation corresponds to the extreme value of the minimum total potential energy, the equilibrium of the system is stable if the total potential energy of the conservative system is a minimum. Since the external applied forces is the only external source of energy included in the total potential, the virtual infinitesimal change in total potential with respect to a virtual infinitesimal change of the independent variable corresponding to an infinitesimal physical change of the conservative system should be equal to zero. That is
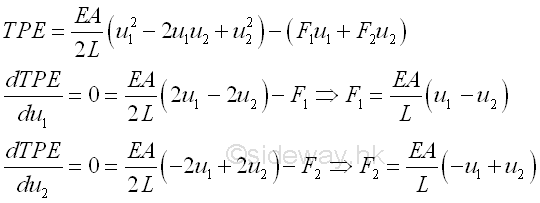
Similarly, the bar can also considered as an element of the system, in which both forces F1 and F2 and displacement u1 and u2 are expressed as one individual element. This can be done by expressing the two force equations in matrix form as the force analysis approach before. That is
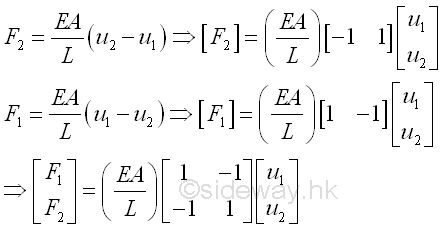
.
©sideway
ID: 140600016 Last Updated: 6/28/2014 Revision: 0 Ref:
References
- Paulo Ribenboim, 2000, My Numbers, My Friends: Popular Lectures on Number Theory
- Kenneth H. Rosen, 2012, Discrete Mathematics and Its_Applications
Latest Updated Links
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 22
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
FiniteElement 2
Natural Sciences
Matter 1
Electric 27
Biology 1
