Content
Number
Decimal
Number and Number Line
Rational
Number
Irrational
Number
Prime, Composite & natural
Complex Number
Decimal Notation & Binary Notation
Number
In general, number is used as the representation of a quantity. And the word "number" is usually refers to the member of a given set of numeral system. The most widely used numeral system is the decimal numeral system which has ten as its base. The notational symbols that represents a number is called numerals. The numerals of a decimal numeral system are 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. The notational symbol "0" can also be considered as an empty place holder.
Decimal Number and Number Line

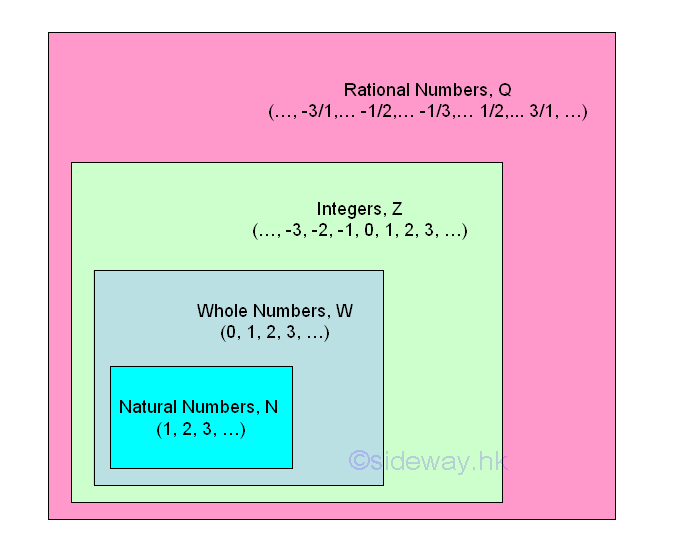
The decimal numeral system is an ordered number set. Every number can be graphically represented by a point on a number line. After defining a position on the straight line as the zero point and a unit length of the straight line as one unit length, then points can be added starting from the zero point on the line through marking the unit length on the line repeatedly. Each point is associated with the number of counting the unit length with positive numbers are to the right of zero and negative numbers are to the left of zero. Numbers are orderly located on the line geometrically with the number on the right is always greater than the number on the left. Number to the right of zero is the counting numbers e.g. 1,2,3... and is called natural numbers. Sometimes zero is included to the set of natural numbers N, but the set of number including zero is called Whole number. And the set of numbers marked on the number line of one unit length apart starting from zero, e.g. -3,-2,-1,0,1,2,3, is called integer Z.

An integer is also called a whole number, i.e. no fraction, which can be positive, negative, or zero. Numbers can then be grouped into
-
integers: ...,-3,-2,-1,0,1,2,3,...
-
positive integers: 1,2,3,...
-
nonnegative integers: 0,1,2,3,...
-
nonpositve integers: 0,-1,-2,-3,...
-
negative integers: -1,-2,-3,...
Rational Number

Since the unit length between two successive numbers is not equal to zero, more numbers can be inserted between points of integers. The most effective method of inserting point to the line segment is by method of equal division. For example, 9 more points or numbers can be obtained by dividing the number between 0 and 1 into ten equal divisions, the numbers from left to right are 0.1=1/10, 0.2=2/10,...,0.9=9/10. More numbers on the number line can also be obtained similarly, e.g. 1/3, 2/3. The numbers on both ends can be expressed as a fraction p/q, e.g. 0=0/10, 1=10/10. These numbers are called rational numbers Q, which can be expressed as a fraction p/q where p and q are integers, and p and q have no common divisor other than one. Therefore integers are a subset of rational numbers
Irrational Number
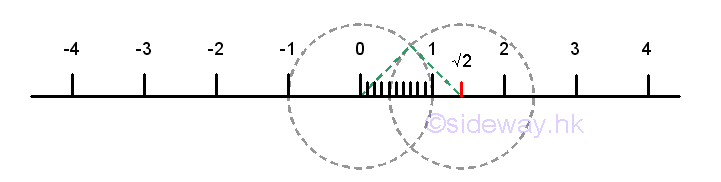
Although, much more points can be plotted on the number line using the method of equal division, the rational number points cannot fill up the number line. There are points on the number line that cannot be expressed as a fraction p/q. For example, √2. The position of the point √2 on the number line can be located using the pythagorean theorem by constructing a right angle triangle with two sides equal to one unit length with the hypotenuse equals to √2. The point at √2 is not a rational point and can be proved by contradiction. If √2 is a rational , then √2 can be expressed as a fraction p/q. Imply
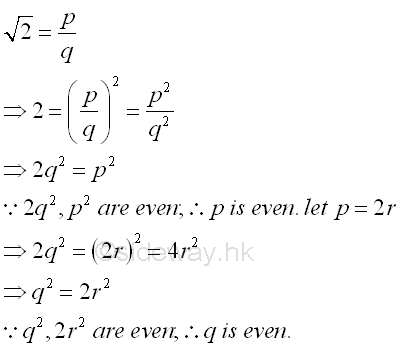
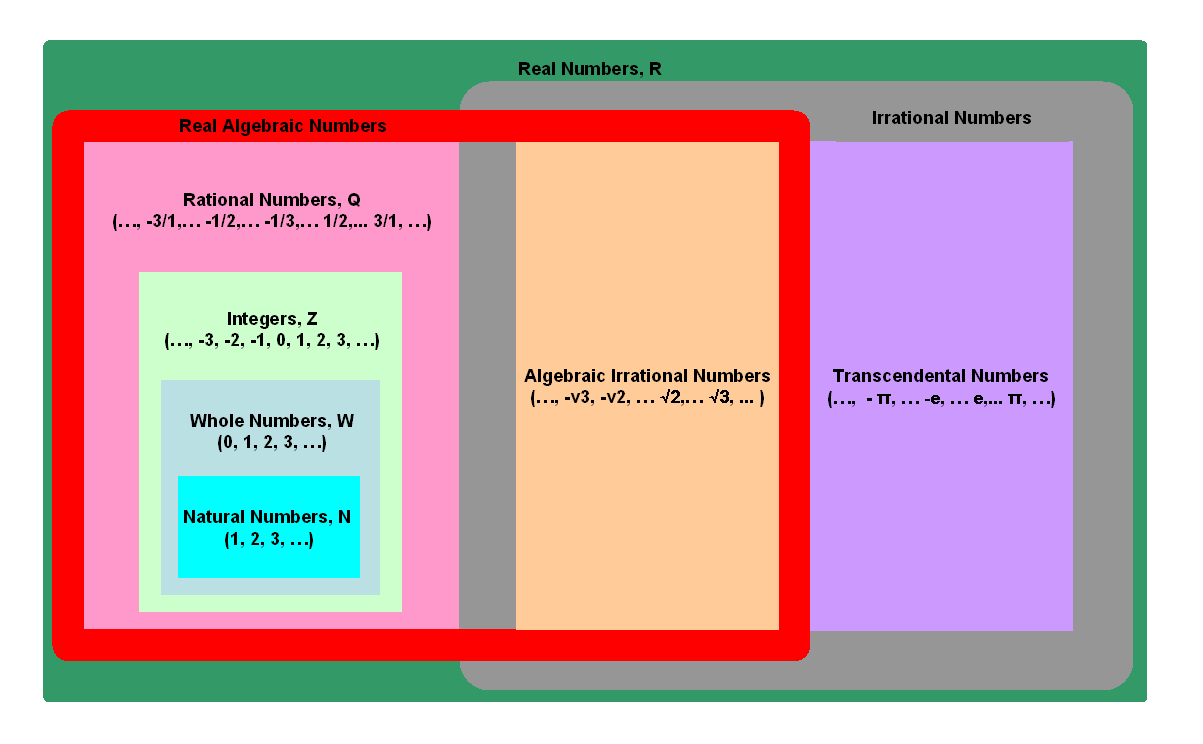
Both p and q are even, 2 is a common factor of p and q. Through the repetition of steps, 2 is always the common factor of the numbers generated. Since p and q always have an even common factor, this contradicts the definition of rational and the assumption that √2 is a rational is false. The point cannot be expressed as a fraction p/q is called irrational point. There are many other examples of irrational points, for example, √3, √5,... Numbers associated with these irrational points that cannot be expressed as a fraction p/q numbers are called irrational number Ir. Therefore √2 is an irrational number from algebraic operation. There are another type of irrational numbers, for example, π, e,... These non-algebraic irrational numbers are called transcendental numbers because they are not the root of any integer polynomial. The set of rational numbers Q and the set of irrational numbers I together form the set of real numbers R.
Prime, Composite & natural
The number line concept of the number system provides the big picture of the real number system. Besides the classification of numbers into sets of natural numbers, integers, or real numbers. One important type of number classification is the set of prime numbers, composite numbers, and the naturals. Prime numbers are natural numbers, e.g. 2, 3, 5, 7,..., which can only be divided by 1 and itself. For other natural numbers, neither 1 nor prime number, they are called composite numbers. In general, a composite number can be expressed as a product of two factors, i.e. n=xy. 1 is not a prime because 1 can only be divided by 1 and 1 has one divisor, 1 only. Besides, prime numbers are always positive numbers. And 1 and 0 are neither prime nor composite. 1 and 0 are naturals to represent yes and no, true and false only.alse only.
Complex Number
Besides the one dimensional number line concept to reprsent a number system, there is also another common two dimensional plane concept to represent a complex number on a complex plane with the horizontal axis representing the real part and the vertical axis representing the imaginary part. A complex number can also be a root of an integer polynomial.
By introducing the concept of complex number, an algebraic number can be any complex number including real numbers which is a root of a non-zero polynomial equation in one variable. While those real and complex numbers thar are not algebraic are classified as transcendental numbers.
Decimal Notation & Binary Notation
A decimal numeral system uses ten numerals, 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9 to denote a natural number n. But for a binary numeral system, only numeral 0 and 1 are used to denote any natural number n.
©sideway
ID: 130400006 Last Updated: 6/3/2018 Revision: 1
Latest Updated Links
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)
- Tefal BL83SD PerfectMix Cook Blender(last updated On 11/25/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/24/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/23/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/22/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
