Content
Primes
Sieve of Eratosthenes
Sieve of
Sundaram
Sieve of
Atkin
Primes
A prime is defined as natural number that can only be divided by 1 and itself. For examples, numbers 2, 3, 5, 7,... are primes. Prime numbers are one of the important types of numbers but there is no easy way to identify or find prime numbers.
Sieve of Eratosthenes
The sieve of Eratosthenes is a simple ancient algorithm developed by Eratosthenes to identify all prime numbers by eliminating all multiples of found primes in any given limit, n iteratively.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| … | … | … | … | … | … | … | … | … | … |
The concept of the sieve of Eratosthenes is simple but the sieve method is more complicated to be implemented.
-
The first step to generate an incremental sequence of positive consecutive integers with n elements.
-
Since number 1 is neither prime nor composite, number 1 is ignored by the sieve.
-
As number 2 is the smallest number in the list, by definition, number 2 must be the first prime of the incremental sequence.
-
The sieving mechanism is to cross off all multiples of found prime in the list of remaining numbers iteratively.
-
According to the mechanism of sieve of Eratosthenes, only the remaining numbers on the list are sieved. In other words, the first multiple of the prime p to be cross off is equal to p as all multiples smaller than prime p have already been sieved by those found primes smaller than p. And therefore the last or largest sieving prime p is also limited to the floor of square root of n because all multiples of primes after have already been crossed off.
-
However, there is no simple way to prevent the repeating crossing off problem as crossing out the number in the table of sieve of Eratosthenes.
-
Primes less than or equal to a given limit n are in the list of the remaining numbers after sieving
Sieve of Sundaram
The sieve of Sundaram is a simple deterministic algorithm developed by Sundaram in 1934 for determining all prime numbers except number 2 up to any given n by eliminating all number of the form i+j+2ij within the limit, the floor of (n-1)/2 iteratively and then doubling and increaseing the remaining numbers by one. The two typical ideas are the elimintion of even numbers which are divisible by number 2 and all odd numbers except number 1 are expressed as an arithmetic progression. For example, numbers eliminated in n=200 with limit equals to 99.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 |
Determined primes are
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 |
| 121 | 122 | 123 | 124 | 125 | 126 | 127 | 128 | 129 | 130 |
| 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | 139 | 140 |
| 141 | 142 | 143 | 144 | 145 | 146 | 147 | 148 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 156 | 157 | 158 | 159 | 160 |
| 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 |
| 171 | 172 | 173 | 174 | 175 | 176 | 177 | 178 | 179 | 180 |
| 181 | 182 | 183 | 184 | 185 | 186 | 187 | 188 | 189 | 190 |
| 191 | 192 | 193 | 194 | 195 | 196 | 197 | 198 | 199 | 200 |
The sieving concept of sieve of Sundaram is similar to the crossing off composite numbers mechanism used in sieve of Eratosthenes. Instead of sieving the whole list of the given limit n, sieve of Sundaram only sieves the odd number of the list, and all odd numbers except number 1 are rearranged in an increasing order from one to floor of n/2.
-
Since number 1 is neither prime nor composite, number 1 is ignored by the sieve.
-
The first step to generate an incremental sequence of positive consecutive integers with floor of n/2 elements starting from one to floor of n/2 to represent all odd numbers except number 1.
-
The sieving mechanism is to cross off all numbers of the form i+j+2ij where 1≤i≤j, in the list of remaining numbers iteratively. The form is
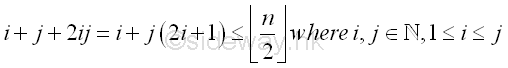
-
Although, all even numbers are excluded in the list, there is still no simple way to prevent the repeating crossing off problem as crossing out the number in the table of sieve of Sundaram as in sieve of Eratosthenes.ber 1 is ignored by the sieve.
-
Primes less than or equal to a given limit n are obtained by doubling all remaining numbers in the list of the after sieving and then increasing all numbers by one.
The sieve of Sundaram is based on sieving the composite odd numbers since all even numbers are ignored. Since an odd number can be expressed as 2k+1, the odd number sequence can therefore be expressed as an ordered sequence in term of k. Let 2i+1 and 2j+1 be any two odd numbers. Therefore any composite odd number can be expressed as (2i+1)(2j+1)=2(i+j+2ij)+1. In other words, all composite number with sequence number k equal to i+j+2ij must be composite odd numbers. Since the sieving mechanism is an iterative operation to sieve all possible composite odd number in the list. The remaining sequence numbers in the list must be prime odd numbers.

Sieve of Atkin
The sieve of Atkin is a simple algorithm developed by Atkin and Bernstein in 2004 to find all prime numbers by eliminating all multiples of number 2, 3, and 5, and testing iteratively with an irreducible binary quadratic equation to which the numbers of solution must be odd providing that the number is a squarefree numbers, in any given limit, n. The first part of the algorithm making use of the idea of sieve of Eratosthenes to eliminate must of the composites which are multiples of number 2, 3, and 5, in the list. The second part of the algorithm making use of the properties of the irreducible binary quadratic form of a number to test where a number is a squarefree composite or not, instead of checking the divisibility of a number.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | 112 | 113 | 114 | 115 | 16 | 117 | 18 | 119 | 120 |
| 121 | 122 | 123 | 124 | 125 | 26 | 127 | 28 | 129 | 130 |
| 131 | 132 | 133 | 134 | 135 | 36 | 137 | 38 | 139 | 140 |
| 141 | 142 | 143 | 144 | 145 | 46 | 147 | 48 | 149 | 150 |
| 151 | 152 | 153 | 154 | 155 | 56 | 157 | 58 | 159 | 160 |
| 161 | 162 | 163 | 164 | 165 | 66 | 167 | 68 | 169 | 170 |
| 171 | 172 | 173 | 174 | 175 | 76 | 177 | 78 | 179 | 180 |
| 181 | 182 | 183 | 184 | 185 | 86 | 187 | 88 | 189 | 190 |
| 191 | 192 | 193 | 194 | 195 | 96 | 197 | 98 | 199 | 200 |
| … | … | … | … | … | … | … | … | … | … |
Remaining numbers are divided into 3 groups with each number congruent to 1 modulo 4, 1 modulo 6, and 11 modulo 12. In order to have a common arithmetic progression, three sets of modulo 60 residues are {1,13,17,29,37,41,49,53}, {1,7,13,19,31,37,43,49}, and {11,23,47,59} .
©sideway
ID: 140600001 Last Updated: 6/6/2014 Revision: 0
Latest Updated Links
- Travel Singapore Sight Central(last updated On 1/8/2026)
- Panasonic HHGTQ1001B13 LED Floor Light(last updated On 1/7/2026)
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 38
Reference 79
Hardware 55
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
