The Euclid's Elements of Geometry

Geometry is the study of figures. Euclid's Elements provides the most fundamental way of learning geometry geometrically.

Book I

Book I of Elements introduces the fundamental elements and notionsof geometry.

Definitions

The definition part is used to introduce the notion of point, line and surface, and the fundamental geometric figures which is defined as a set of loci of points on a plane with boundary of one, or boundaries of three, and four lines that can be constructed by means of a rule and a compass. And finally the parallel concept between two lines by which more than one line is needed in order to bound a geometric figures.

1. A point is that which has no part.
   Remarks: A point A is the notion of position with no length, breadth, and thickness.
2. A line is a length which has no breadth, and thickness.
   Remarks: A curved line a is the notion of locus, which is constructed by means of a rule and a compass, with breadthless length. In other word, a line may be straight, curved, or the combination of straight and curved. In general, a line may be not on the same plane.
3. The extremities of a line are points.
   Remarks: Points A and B are located at the ends of a line a to locate the position of endings of the line.
4. A straight line is a line which lies evenly with the points on itself.
   Remarks: Let points A and B are located at the ends of a straight line a, points can be evenly located on the straight line by means of a rule and a compass on the plane, where points A and B are located, in any way.
5. A surface is that which has length and breadth only.
   Remarks: A surface α is the notion of an area of loci of points, which is made up of length and breadth, but no thickness. Similar to the notion of a line, a surface may be in irregular shape and not on the same plane,
6. The extremities of a surface are lines.
   Remarks: A surface α is bounded by a line which is made up of lines a, b, c, andd. And in turn these lines are bounded by points A, B, C, and D.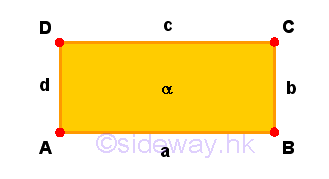
7. A plane surface is a surface which lies evenly with straight lines on itself.
   Remarks: A plane surface α must be bounded by lines on the same plane. Let lines a, b, c, and d are the extremities of the plane surface α but not necessary be straight lines. Let points A, B, C, and D are located at the ends of lines a, b, c, and d. Since point A, B, C, and D are located on the same plane, straight lines can alway be constructed by means of a rule and a compass on the same plane from one extremity to another extremity. As points can be evenly located on the straight line, straight lines can also be constructed in the similar manner on the plane surface evenly in any way.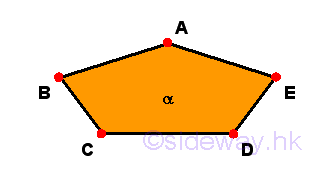
8. A plane angle is the inclination of two lines to one another when the two lines in a plane meet one another and are not lying in a straight line.
   Remarks: In a plane surface α, there exists some straight lines, e.g. lines a and b or AB and BC, that meets at a common point, e.g. B and incline to one another at an angle, e.g. θ. The angle of inclination between two lines on the same plane is called plane angle, i.e the angle θ. But in general case, there always are two ways to denote the angle of inclination between two crossed lines, so angle θ is also called ∠ABC in terms of three points.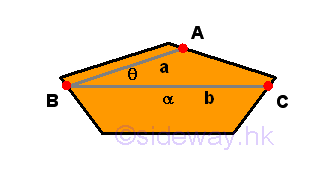
9. An angle is called rectilineal angle when the angle contained by the lines are straight.
   Remarks: Assume lines a and b or AB and BC lie on the same plane and meet at a common point B. If both lines AB and BC are straight lines, then the type of contained angle θ or ∠ABC is called rectilineal angle. In this case, there are also two ways to denote a rectilineal angle, but only the smaller angle are considered.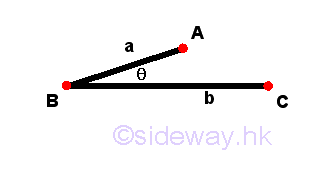
10. Each of the adjacent angles making by a straight line standing upon another straight line is called right angle when these adjacent angles are equals to one another. And this condition of the straight line standing on the other is called a perpendicular to that on which the straight line stands.
    Remarks: Assume straight lines a and b or AB and CD lie on the same plane and straight line b stands upon straight line a. Point C is also a common intersecting point of both straight lines. Since there are a common straight line CD and a common point C for the angles, ∠ACD and ∠BCD, two angles are adjacent angles. Since there is one and only one condition of the two adjacent angles equal to one another upon a straight line, a special name, perpendicular, is used to name this condition, that is the straight line CD is a perpendicular to the straight line AB, and a special name, right, is also given to each of the adjacent angles.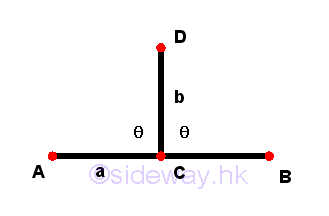
11. An obtuse angle is an angle greater than a right angle.
    Remarks: Assume a line c or EC is added to the system of lines at definition 10. If the line c lies on the same plane and meets at the common point C, then lines b and c incline to one another at an angle, e.g. ϕ or ∠ECD. In Euclid's geometry, angles are usually refered to the magnitude of angle less than two right angles. The angle of inclinaton is called obtuse angle, when the magnitude of an angle ϕ or ∠ECD is greater than a right angle but less than two right angles. In general, an obtuse angle can also be used to describe a non-rectilineal angle.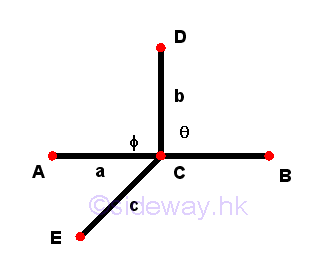
12. An acute angle is an angle less than a right angle.
    Remarks: Assume a line d or FC is added to the system of lines at definition 11. If the line d lies on the same plane and meets at the common point C, then lines b and d incline to one another at an angle, e.g. σ or ∠FCD. In Euclid's geometry, angles are usually refered to the magnitude of angle less than two right angles. The angle of inclinaton is called acute angle, when the magnitude of an angle σ or ∠FCD is less than one right angles. In general, an acute angle can also be used to describe a non-rectilineal angle.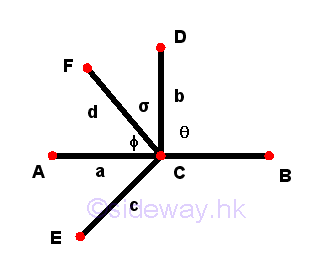
13. A boundary is that which is an extremity of anything.
    Remarks: Further to definitions 3 and 6, a more general term, boundary, is used to name the set of of loci of points at the extremity of anything. For example: Lines a, b, c, d, e, f, g, and h are the boundaries of the surface α. Points A, B are the boundary of line a, points B, C are boundary of line b, points C, D are boundary of line c,... etc.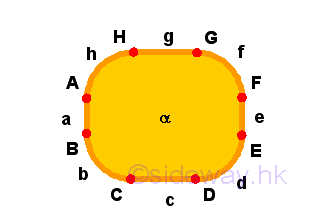
14. A figure is that which is contained by any boundary or boundaries.
    Remarks: Figure is a general term used to name the set of of loci of points contained by any interested boundary or boundaries. For example: Surface α is a figure which is contained by the boundary, line a.
15. A circle is a plane figure contained by one single line, such that all the straight lines falling upon the line radiating from one single point among those lying within the figure are equal to one another.
    Remarks: Circle is a name given to a plane figure α contained by a boundary with one single line a to which there is alway one single point within the figure such that all the straight lines, e.g. line b, radiating from the point, e.g. point A, to a point, e.g. point B, of the line of boundary, e.g. line a, are all equal to one another.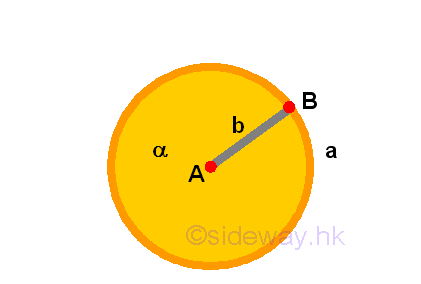
16. The point of which straight lines radiating from is called the centre of the circle.
    Remarks: The point A, from which striaght lines radiating to the boundary of the figure, on the circle figure α is called the centre of the circle. From another point of view, the point A is also the centre of the boundary line a.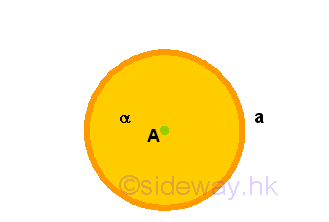
17. A diameter of a circle is any straight line being drawn through the centre and terminated in both directions by the circumference of the circle. Such a straight line also bisects the circle.
    Remarks: Any straight line c drawn throught the centre and terminated in both directions by the circumference of the circle α can be considered as two straight lines radiating from the centre to the boundary of the circle. Therefore, the straight line c is equal to two straight radiating lines b and is the maximum distance between two points on the circumference of the circle. This type of straight line is called diameter of a circle. Since two straight radiating lines b can always be constructed, which are prependicular to the diameter, on the two divided half sides of the circle, the diameter of a circle must bisect the circle.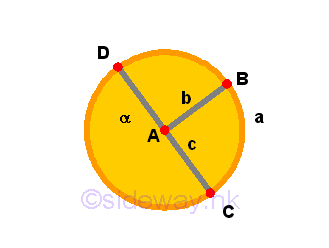
18. A semi-circle is the figure contained by the diameter and the circumference cuts off by the diameter. The center of the semi-circle is the same point as the centre of the circle.
    Remarks: A semi-circle α is simply the name given to the figure contained by diameter c and the circumference a cuts off by the diameter d. And the centre of the circle is still the point from which striaght lines radiating to the boundary, line a, of the semi-circle. Unlike circle, a semi-circle is made up of a straight line and a curved line.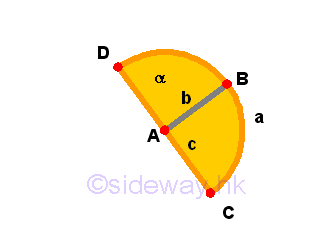
19. Rectilineal figures are those figures contained only by straight line. Trilateral figures are those being contained by three, quadrilateral are those contained by four, and multilateral are those contained by more than four straight lines.
    Remarks: For those figures contained only by straight line with no curved boundary, these figures are called rectilineal figures. A semi-circle is not a rectilineal figure. For those figures contained by only three straight lines with no curved boundary, these rectilineal figures are called trilateral figures. For those figures contained by only four straight lines with no curved boundary, these rectilineal figures are called trilateral figures. For those figures contained by more than four straight lines with no curved boundary, these rectilineal figures are all named by the general name multilateral figures.
20. Of the trilateral figures, an equilateral triangle is that having three equal sides, an isosceles triangle having only two equal sides, and a scalene triangle having three unequal sides.
    Remarks: When considering the magnitude of the sides of a trilateral figure, trilateral figures can be classified into three groups, equilateral triangle, isosceles triangle, and scalene triangle. When a trilateral figure has three equal sides, these trilateral figures are called equilateral triangle.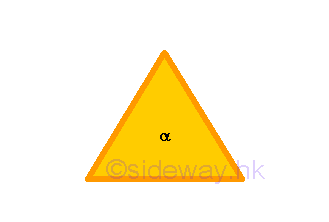  When a trilateral figure has two equal sides,these trilateral figures are called isosceles triangle. 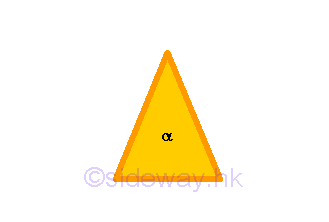When a trilateral figure has no equal sides, that is three unequal sides, these trilateral figures are called scalene triangle.
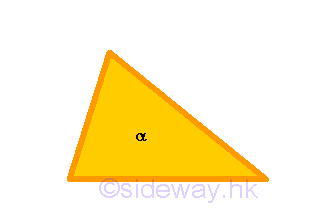
21. Further of the trilateral figures, a right-angled triangle is that having a right-angle, an obtuse-angled triangle having an obtuse angle, and an acute-angled triangle having three acute angles.
    Remarks: When considering the magnitude of the angles of a trilateral figure, trilateral figures can be classified into three groups, right-angled triangle, obtuse-angled triangle, and acute-angled triangle. When a trilateral figure has a right angle, these trilateral figures are called right-angled triangle.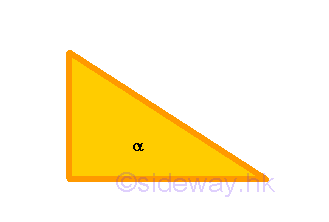 When a trilateral figure has an obtuse angle, these trilateral figures are called obtuse-angled triangle. When a trilateral figure has three acute angles, these trilateral figures are called acute-angled triangle.
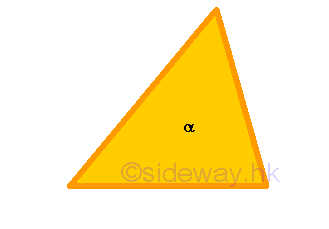
22. Of the quadrilateral figures, a square is that which is right-angled and equilateral, a rectangle or oblong is right-angled but not equilateral, a rhombus is equilateral but not right-angled, and a rhomboid is having opposite sides and angles equal to one another which is neither right-angled nor equilateral. Quadrilateral figures besides these features is trapezia.
    Remarks: For the quadrilateral figures, there are many way to construct the figures by using four straight lines. But if the angles of the quadrilateral figures are only classified according to all right angled or not-all right angled, the classification of quadrilateral figures becomes much simpler. When considering the magnitude of both the sides and the right-angledness of a quadrilateral figure together, quadrilateral figures may be classified into five groups, square, rectangle or oblong, rhombus, rhomboid, and trapezia. When a quadrilateral figure has 4 right angles and 4 equal sides, these quadrilateral figures are called square. When a quadrilateral figure has 4 right angles but 4 sides are not equilateral,these quadrilateral figures are called oblong or rectangle. When a quadrilateral figure has no right angles but 4 sides are equilateral, these quadrilateral figures are called rhombus. When a quadrilateral figure has no right angles and 4 sides are not equilateral, but the opposite sides and angles of the quadrilateral figure are equal to one another, these quadrilateral figures are called rhomboid. When a quadrilateral figure can not be grouped into the above four groups, those quadrilateral figures are called trapezia. But trapezia are usually refered to quadrilateral figure with a pair of parallel straight lines.
23. Parallel straight lines are straight-lines which, being in the same plane, and being produced indefinitely in both directions, do not meet one another in neither directions.
    Remarks: When two straight lines, which lie in the same plane, do not meet one another in neither directions when being produced indefinitely, the two straight lines are parallel to each other.

Postulates

1. To draw a straight line from any point to any point.
   Remarks: For any given two points, A and B, a straight line a can be always be drawn from point A to point B with the extremities point A and point B.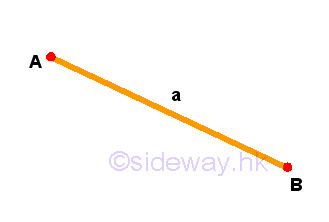
2. To produce a finite straight line continuously in a straight line
   Remarks: For any straight line, a, the line itself can be always be drawn from a point A to another point B, and to point D of any finite length in a straight line continously, or in other direction from a point B to another point A, and to point D of any finite length in a straight line continously.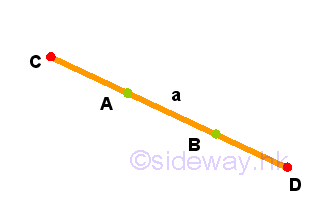
3. To describe a circle with any centre and distance.
   Remarks: From the properties of a circle figure, any circle figure α can be constructed by a compass with a given point A of the centre of circle and a given distance of the radiating line a between the two extremeities.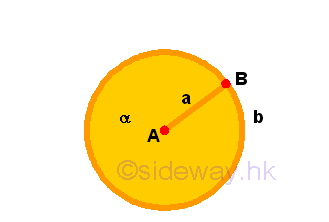
4. That all right angles are equal to one another.
   
5. If a straight line falling across two straight lines makes internal angles between the two straight lines on the same side less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which sum of internal angles less than two right angles.
   

Common Notions

1. Things equal to the same thing are also equal to one another.
2. If equals are added to equals, then the wholes are equal.
3. If equals are subtracted from equals, then the remainders are equal.
4. Things which coincide with one another equal one another.
5. The whole is greater than the part.