Content
Quadratic Equations
Roots of Quadratic Equations[1]
Quadratic Formula of Quadratic Equations[1]
Discriminant of Quadratic Equations[1]
Alternate Form of Quadratic Formula
Forms of Quadratic Function
Sign of Quadratic Expression[1]
Quadratic Equations
A quadratic function is a polynomial function in a single variable, x, of the form equivalent to f(x)=ax2+bx+c with a≠0. The expression of a quadratic function is therefore called a polynimial of degree 2, or the second order or second degree polynomial with the highest exponent of the single variable, x equal to 2. And a quadratic equation is any equation of the form equivalent to ax2+bx+c=0 by setting the quadratic function equal to zero. Therefore a quadratic equation is only a typical example of a quadratic function.
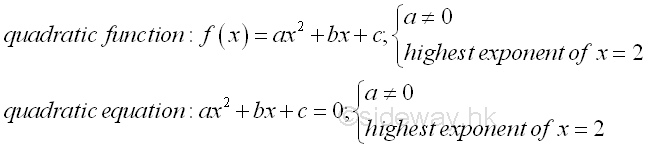
Roots of Quadratic Equations[1]
The solutions of a quadratic equation is also called roots of a quadratic equation. Since a quadratic equation is a second order polynomial equation, a quadratic equation must has two solutions according to the fundamental theorem of algebra. In general, the solution may be both real, or both complex. Assume α and β are the roots of the quadratic equation, ax2+bx+c=0, the quadratic equation can then be written as (x-α)(x-β)=ax2-(α+β)x+αβ=0, imply (α+β)=-b/a and αβ=c/a by equating the coefficients of two polynomials.
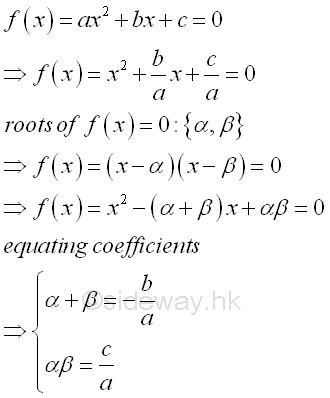
Quadratic Formula of Quadratic Equations[1]
Analytically, the solutions of quadratic equation can be found by the method of "completing the square". The idea of determining the roots of a quadratic equation is making use of the symmetry of the quadratic function g(x) about a vertical axis parallel to the y-axis by transforming the quadratic equation f(x)=0 into a symmetry quadratic function g(x). The obtained formula for calculating the roots of the quadratic equation is called the quadratic formula. Imply
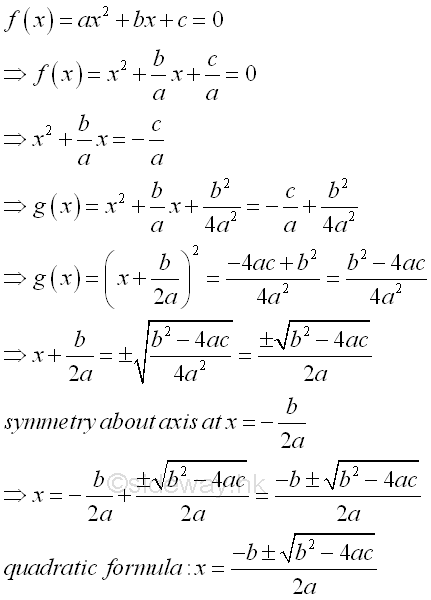
Assuming α≥β then the values of the α and β are
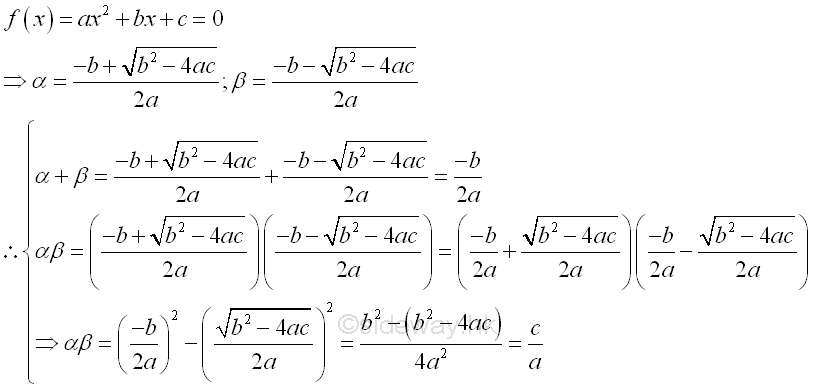
Discriminant of Quadratic Equations[1]
According to the quadratic formula, the roots of a quadratic equation is charactered by the square root components of the quadratic formula. Depending on the value of expression (b2-4ac), the roots of a quadratic equation can be coincident, rational, real or complex numbers. And (b2-4ac) is therefore called the discriminant of the quadratic equation. In general, the discriminant, b2-4ac, can have four cases:
-
b2>4ac, imply discriminant, b2-4ac>0, if b2-4ac is a perfect or complete square then two distinct roots are rational.

-
b2>4ac, imply discriminant, b2-4ac>0, if b2-4ac is not a perfect or complete square then two distinct roots are real or irrational.

-
b2=4ac, imply discriminant, b2-4ac=0, two roots are rational and coincident. That is two equal roots, one double root or one single solution.
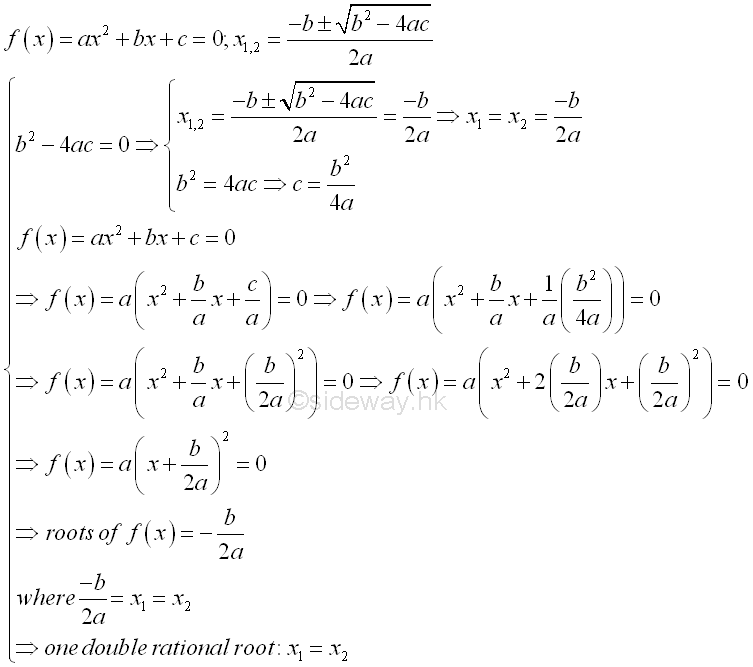
-
b2<4ac, imply discriminant, b2-4ac<0, two distinct roots are complex or imaginary.

Alternate Form of Quadratic Formula
The quadratic equation is obtained by setting the quadratic function equal to zero and x is not equal to zero, the quadratic formula can be derived in an alternative way.

Forms of Quadratic Function
The quadratic function f(x)=ax2+bx+c is usually called the standard form of a quadratic function. Since a quadratic equation has two roots, the standard form of a quadratic function can be expressed in terms of the two roots, f(x)=a(x-x1)(x-x2), called factored form.
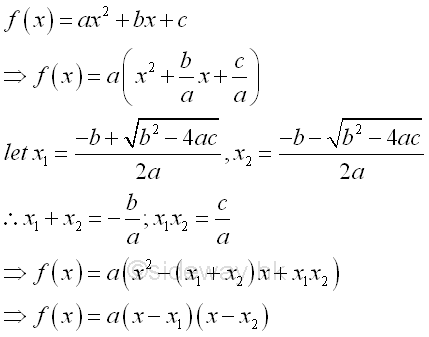
Besides the quadratic function is symmetric about a line, the standard form of a quadratic function can be expressed in terms of the vertex of the function, f(x)=a(x-x0)2+y0, called vertex form.
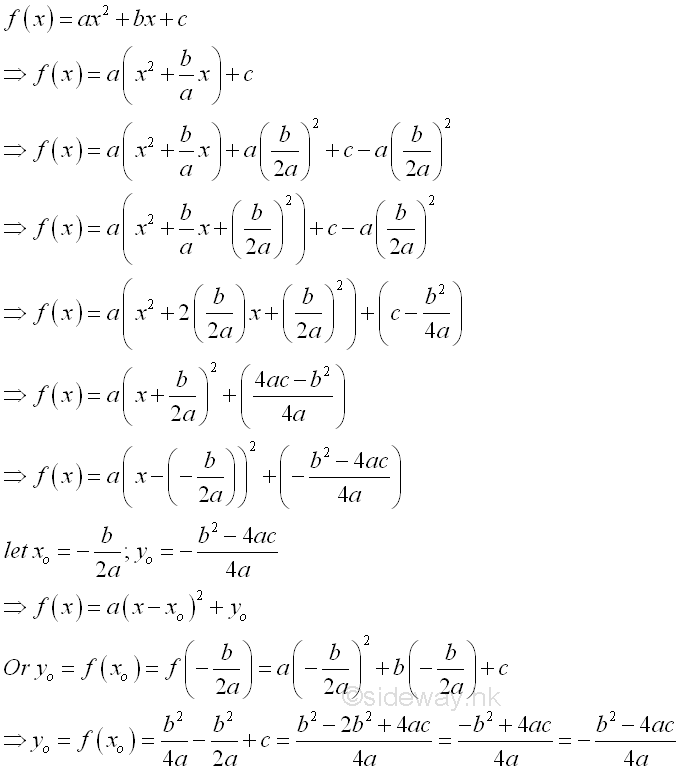
Sign of Quadratic Expression[1]
Let E be the quadratic expression of the quadratic function f(x)=ax2+bx+c. If α and β are the roots of quadratic equation ax2+bx+c=0 and α≥β, then the sign of the quadratic expression can also be determined accordingly. In general, assuming the quadratic expression with two distinct real roots, when a is positive, E is positive if x>α or x<β and E is negative if α>x>β. Or when a is negative, E is positive if α>x>β and E is negative if x>α or x<β. In other words, E has same sign as coefficient a for x>α or x<β, and E has opposite sign as coefficient a for α>x>β. This case can also be considered as the case b2-4ac>0 with two distinct real root for the corresponding quadratic equation. Imply

In the case b2-4ac=0 with double real root for the corresponding quadratic equation, this is a special condition of the general case where α equal to β and therefore the condition α>x>β becomes α=x=β is equal to zero. E has the same sign as the coefficient a.
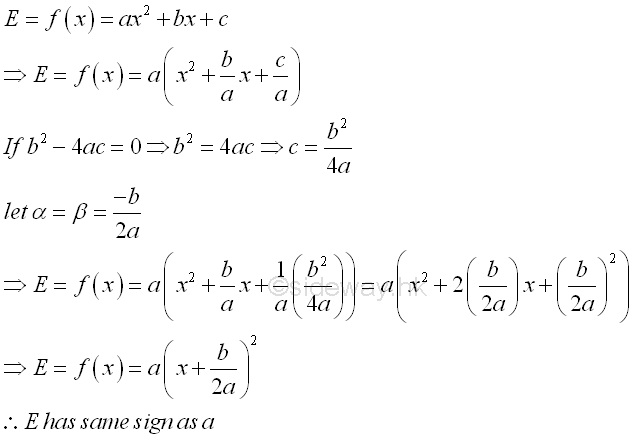
In the case b2-4ac<0 with two distinct complex root for the corresponding quadratic equation, this is a special condition of the general case where quadratic expression, E, does not equal to zero for all real x. E has the same sign as the coefficient a..
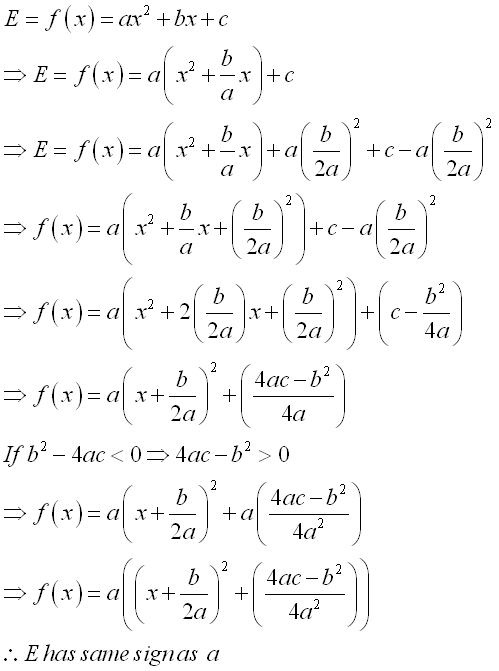
©sideway
ID: 130500017 Last Updated: 5/17/2013 Revision: 0 Ref:
References
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
- Wheatstone, C., 1854, On the Formation of Powers from Arithmetical Progressions
- Stroud, K.A., 2001, Engineering Mathematics
- Coolidge, J.L., 1949, The Story of The Binomial Theorem
Latest Updated Links
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/10/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 26![]()
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
