Content
Kinetics: Momentum
Inertia and Mass
Momentum
Newton's Second Law of Motion
Equation of Kinetic Motion
Dynamic Equilibrium
Kinetics: Momentum
Momentum is one of the most important properties in study kinetics.
Inertia and Mass
From the law of inertia, inertia is defined as the tendency of an object to resist a change in motion. Mass, in general, is defined as a quantity to measure the inertia of a body at rest relative to the frame of reference. Besides, in practical sense, mass is also used to denote as the quantity of matter that is the inertial mass of an object. And by the Newton's second law of motion, the external force F changing the motion of an object can be determined by the mass m of the object multiplied by the acceleration a of the object. That is F=ma.
Momentum
Momentum p can be defined as a quantity to measure the inertia of an object in motion relative to the frame of reference. In other words, momentum is defined as a quantity to measure the motion of an object and the tendency of an object's kinetics to resist a change in motion. That is p=mv.
Newton's Second Law of Motion
From Newton's second law of motion, the acceleration of an object due to the force F acting upon an object is proportional to the magnitude of the force and the acceleration is in the direction of the force. In other words, the ratio of the applied force used change to the motion of an object and the acceleration of the object is a constant value. Since this constant value is the characteristic of the measured object, it is called the mass of the object. According to Newton's first law of motion, force is applied upon the object to change the motion of the object, the mass propoerty can be used as a quantitative measurement to measure the tendency of an object to resist a change in motion, mass m of an object can also refer to the inertial mass of an object.
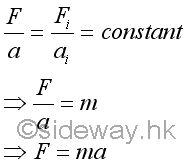
Acceleration is defined as the rate of change of velocity. Therefore force can be expressed in terms of velocity. Since the mass of the object is constant, force can then be expressed in term of the rate of change of the product of mass and velocity. By definition of momentum, the product of mass and velocity is equal to the momentum of the object. In other words, the force F acting upon an object is equal to the rate of change of the momentum of the object.
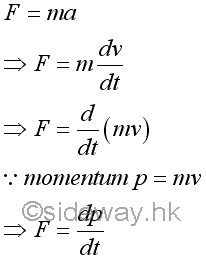
Equation of Kinetic Motion
Through force addition, force acting on an object can be the resultant force of several forces acting on the object simultaneously. That is
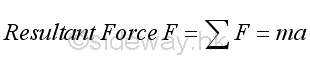
If the resultant force F acting upon an object is equal to zero, the acceleration a of the object must be equal to zero also. In other words, the rate of change of the velocity is equal to zero or the initial velocity remains unchange. That is, if the object is at rest, initial velocity equal to zero, vi=0, the object remains at rest, v=0. If the object is moving with a velocity, initial velocity equal to vi, vi=v0, the object will remain moving at a constant speed v=v0 along a straight line. And this is the statement of Newton's first law of equation.

Similarly, the resultant force is also equal to the rate of change of the momentum of an object. That is
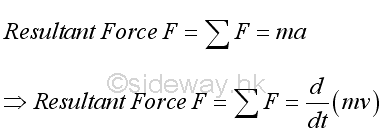
If the resultant force F acting upon an object is equal to zero, the rate of change of momentum is equal to zero. Or the initial momentum remains unchanged in both magnitude and direction. Therefore for an object with no momentum change, the motion of the object does not change its state of motion, either remains at rest or continues to move at a constant velocity. This is an alternative statement of Newton's first law. In other words, force can be converted into momentum, or vice versa. The relationship between force and momentum is the principle of momentum convservation.
Or through force decomposition, force acting on an object can be decomposited according to the interested components. For example, force can be resolved into rectangular components
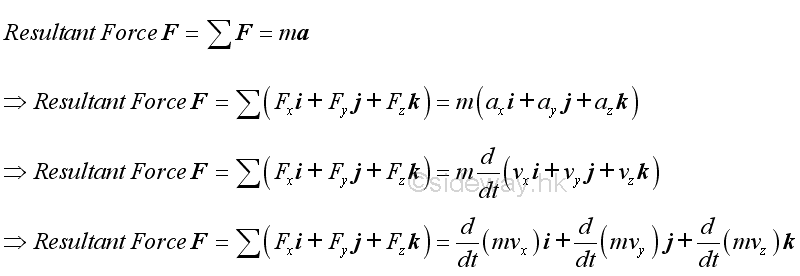
For example, force acting on an object can be resolved into tangential motion with tangential and normal components when the object moves in a plane.

Although momentum play an important role in kinetics, force expressed in term of acceleration is still an important equation of kinetic motion. But all acceleration should be measured with respect to a newtonian frame of reference. For example, in most engineering problems, accelerations can be determined with respect to any coordinate system attached to the earth. However, relative accelerations between objects measured with respect to moving coordinate system of an accelerated body cannot be used in the equations of motion.
Dynamic Equilibrium
In general, resultant force of an object is equal to zero in static equilibrium. Therefore an object can be either at rest or moving in constant velocity when an object is in static equilibrium. Since the kinetic motion of an object can be expressed in terms of force from the equation of kinetic motion, an equivalent negative force vector can be added to the equation of kinetic motion to form alternative form of equation of kinetic motion. Since the resultant force is equal to zero, the alternative form of equation of kinetic motion can be considered as the equation of dynamic equibilibrium. That is
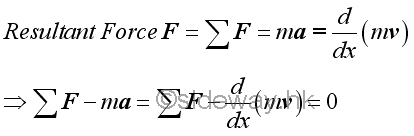
©sideway
ID: 140900003 Last Updated: 9/13/2014 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 37
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
