Content
Kinetics: Linear Momentum and Force
Acceleration of
Particle Object
Newton's Second Law of Motion
Kinetic of Motion
Pendulum
Object on a Banked Curve
Relative Motion
Pulley
Wedge
Kinetics: Linear Momentum and Force
Momentum is used to measure the motion of an object. Momentum is also called linear momentum as momentum is used to measure the instantaneous linear motion of an object. Resultant force is used to measure the rate of change of the momentum of an object. And therefore both force acting upon an object and the acceleration of an object are also important characteristics of an object in motion.
Acceleration of Particle Object
Newton's Second Law of Motion
The rate of change of the momentum of an object can be determined by the resultant force applied on the object using Newton's second law of motion.
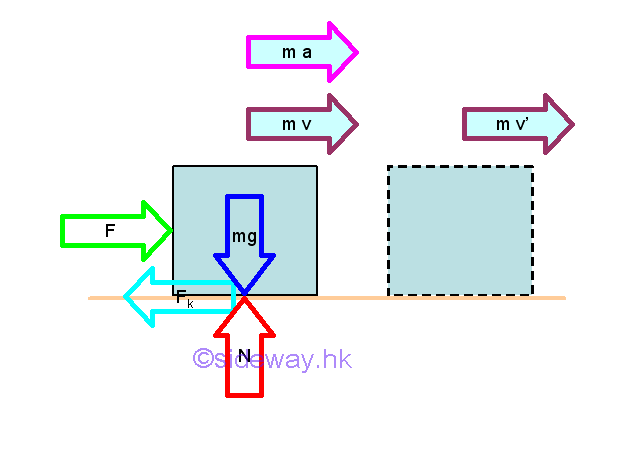
From Newton's second law of motion, an object will be accelerated if the the resultant force acting on it is not equal to zero. Since mass is assumed to be a constant, the rate of change of the momentum of an object is equal to mass time acceleration which is equal to force by definition. In other word, the instantaneuous change in momentum is due to the resultant force. The acceleration of the object is proportional to the magnitude of the resultant force and the acceleration is in the direction of the resultant force.

The velocity of the object can then be determined kinematically.
Kinetic of Motion
Pendulum
For the circular motion of a pendulum, the velocity of the object can be determined by resolving the acceleration vector at the position into tangential and normal components since the normal component of the acceleration is related to tangential velocity of the object.
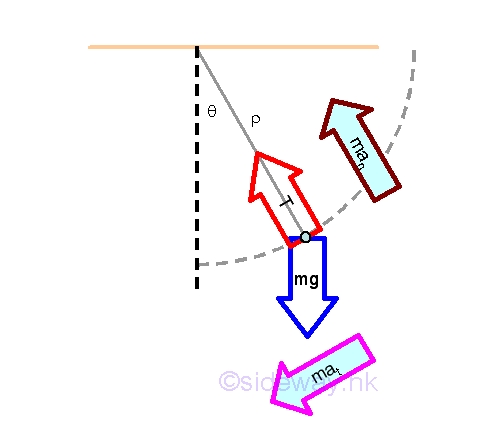
From Newton's second law of motion, an object will be accelerated if the the resultant force acting on it is not equal to zero. The acceleration of the object is proportional to the magnitude of the resultant force, sum of the weight vector and tension vector, and the acceleration is in the direction of the resultant force. From kinematic of circular motion, the normal acceleration component of an object due to the normal component of the resultant force , whch is used to change the direction of motion, is proportional to the square of the tangential velocity and inversely proportional to the radius of curvature at the position accordingly. While the tangential acceleration component is used to change the speed of the tangential velocity.
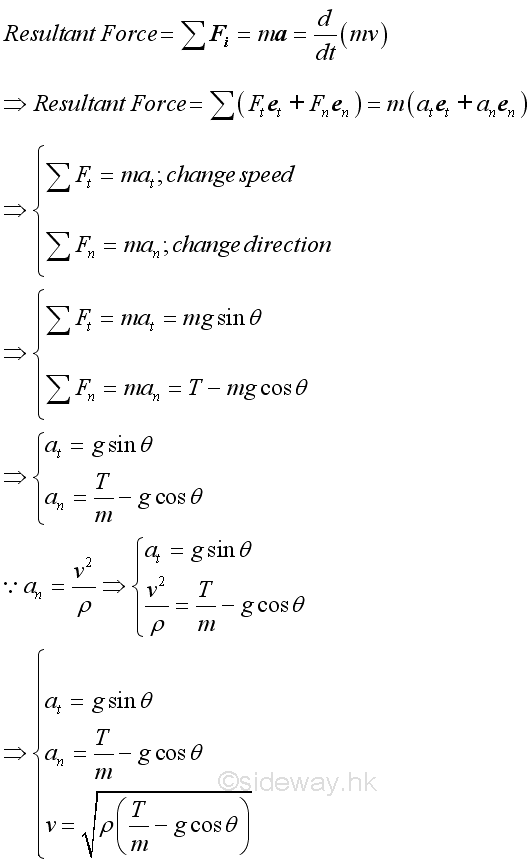
Both the tangential and normal components of the acceleration is a function of angle θ. if the initial tangential velocity of the object is equal to zero, the tension in the cord is then equal to the normal component of the weight of the object. The tension in the cord will be increased as the tangential velocity of the object increases.
Object on a Banked Curve
For the curvilinear motion of an object on a banked curve, the rated speed at which the object moves along the banked curve with no lateral friction force exerted on its, is limited by the banked angle of the curve which provided the lateral stopping force to the object. The rated speed of the object can then be determined by resolving the acceleration vector at the position into tangential and normal components since the normal component of the acceleration is related to tangential velocity of the object.
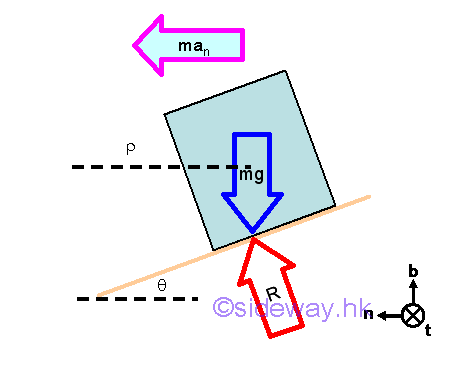
From Newton's second law of motion, an object will be accelerated if the the resultant force acting on it is not equal to zero. The acceleration of the object is proportional to the magnitude of the resultant force, sum of the weight vector and reaction vector, and the acceleration is in the direction of the resultant force. From kinematic of curvilinear motion, the normal acceleration component of an object due to the normal component of the resultant force , whch is used to change the direction of motion, is proportional to the square of the tangential velocity and inversely proportional to the radius of curvature at the position accordingly. While the tangential acceleration component is used to change the speed of the tangential velocity. The binormal component of the resultant force will be equal to zero because the weight of the object will always equal to the binomal component of the reaction.

Velocity v is the rated speed with no lateral friction force. Only the normal component of the acceleration of the object is a function of angle θ. The binormal component of the acceleration is always equal to zero. While the tangential component of the acceleration is the rate of change of the velocity at the position which does not directly affect the instantaneous tangential velocity.
Relative Motion
Pulley
For a pulley system, both the motion of objects and the tension in the cord are related by the configuration of the pulley system.
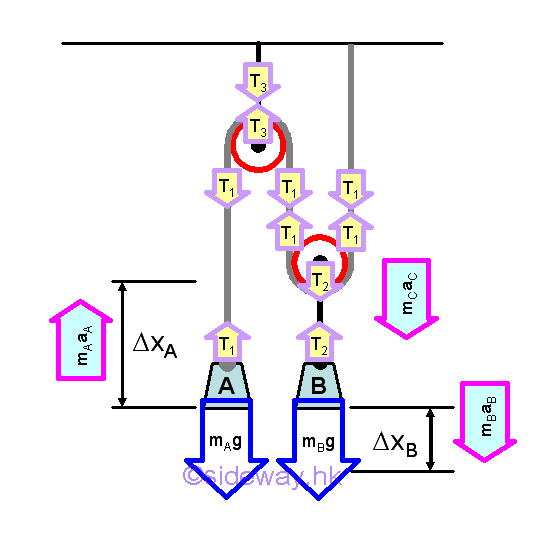
Assume the mass of pulleys and cords are negligible. From Newton's second law of motion, an object will be accelerated if the the resultant force acting on it is not equal to zero. The acceleration of each individual object is proportional to the magnitude of the resultant force acting on it, that is sum of the weight vector and tension vector acting on the object accordingly, and the acceleration is in the direction of the resultant force accordingly also. From kinematic of relative motion, the acceleration of object A and B is related. From the kinetic equilibrium of pully, resultant force acting on it is assumed to be equal to zero since the mass of pulley is assumed to be equal to zero.
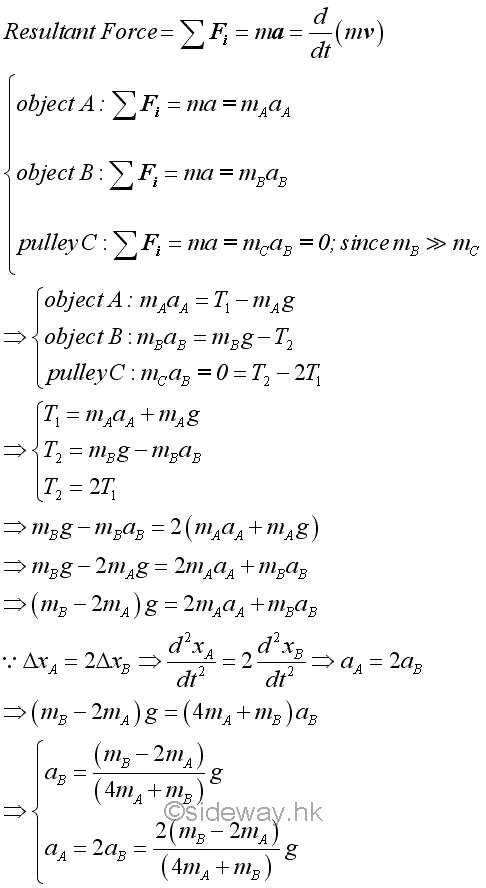
In general, when an object is accelerating, the tension in the cord is not equal to the weight of the object. Tensions acting on the pulley are in equilibrium because the mass of pulley is usually much smaller than the attached load. The acceleration of objects is positive when the mass of object B is greater than 2 times the mass of object A. The acceleration of objects is zero when the mass of object B is equal to 2 times the mass of object A. The acceleration of objects is negative when the mass of object B is less than 2 times the mass of object A.
Wedge
When an object slides smoothly on a wedge from rest, the wedge will move simultaneously if the wedge is supported by a smooth horizontal surface. This is caused by the interaction between two objects.
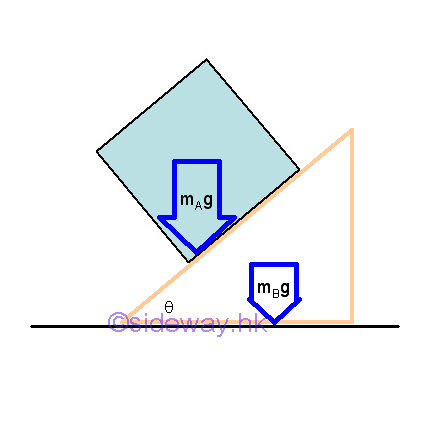
Object A of weight mAg is supported by the reaction force RA , and the component of the resultant force tangent to the slope causes the object A to slide on the wedge. Since object A is sliding and there is no friction force, only the interaction, the reaction force RA between objects A and B and the weight of object B are reacted by the reaction force RB. When object A slide from rest, object A is accelerated relative to the object B along the slope of object B. As object B moves, the object A located on object B will also be moved simultaneously. This is because the interaction force RA between objects A and B will also act on object B.
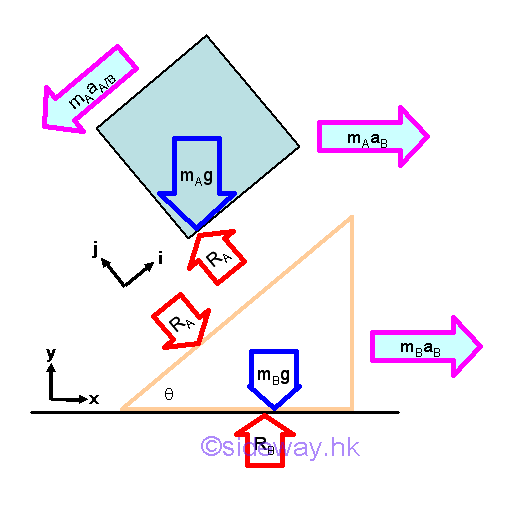
Object A of weight mAg is supported by the reaction force RA, and the component of the resultant force tangent to the slope causes the object A to slide on the wedge. Since object A is sliding and there is no friction force, only the interaction, the reaction force RA between objects A and B and the weight of object B are reacted by the reaction force RB. When object A slide from rest, object A is accelerated relative to the object B along the slope of object B. As object B moves, the object A located on object B will also be moved simultaneously. This is because the interaction force RA between objects A and B will also act on object B. The acceleration of object B is only caused by the reaction RA. Since object B is accelerated, the relative acceleration of object A relative to object A is with respect to an accelerated coordinate system. And the acceleration of object A with respect to a Newtonian or Galilean reference frame is therefore equal to the vector sum of acceleration of object B plus the relative acceleration of object A with respect to object B.

©sideway
ID: 140900004 Last Updated: 9/30/2014 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
