Content
Kinetics: Impact and Momentum
Principle of Impulse and Momentum
Impulse to Stop
the Motion of an Object
Impulses
of a Falling Object when Falling onto a Cart
Impulses to Change the Direction of a Ball
Impact
and Momentum
Impact of Two Free
Objects
Impact of Object
on a Fixed Wall
Impact of a ball on a Constrained Block
Kinetics: Impact and Momentum
Momentum is used to measure the instantaneous linear motion of an object. Impulse is the concept used to cause the change of the momentum of an object over a period of time. When two moving objects collide together, the produced impulsive forces between two objects act and react upon each other such that the momentums of two objects change accordingly. Unlike static applied forces, the impulsive forces are only produced over a very short time interval due to the relative motion of the two objects. During the approaching period of an impact, both objects are deformed by the impulsive forces produced at the area in contact. The impulsive forces vanish when the relative velocity of two objects along with the line of impact is equal to zero. As there is no impulsive force, the diverging period of an impact begins with the restitutive force produced by the restoration of the deformed or compressed object at the point of impact. Therefore the two objects diverge from one another after the collision of an impact.
Principle of Impulse and Momentum
Although the principle of impulse and momentum can be used to solve any problems over a period of time, the concept of impulse is usually used to tackle problems of impulsive motion under an impulsive force over a short time interval. Usually an impulsive force is only used to act upon an object over a short period of time in order to change the momentum of the object.
Impulse to Stop the Motion of an Object
To stop the motion of an sliding object on a frictionless inclined surface by an impulse in a short period of time .

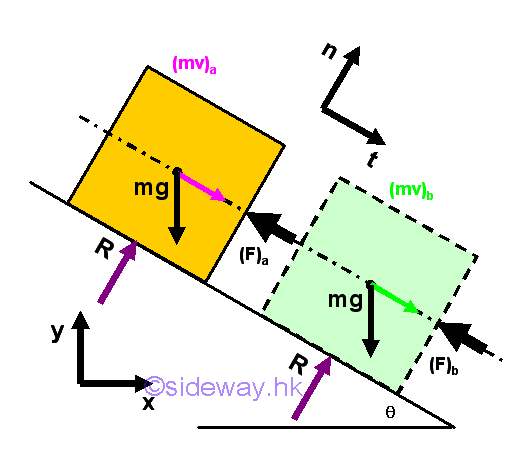
Impulses of a Falling Object when Falling onto a Cart
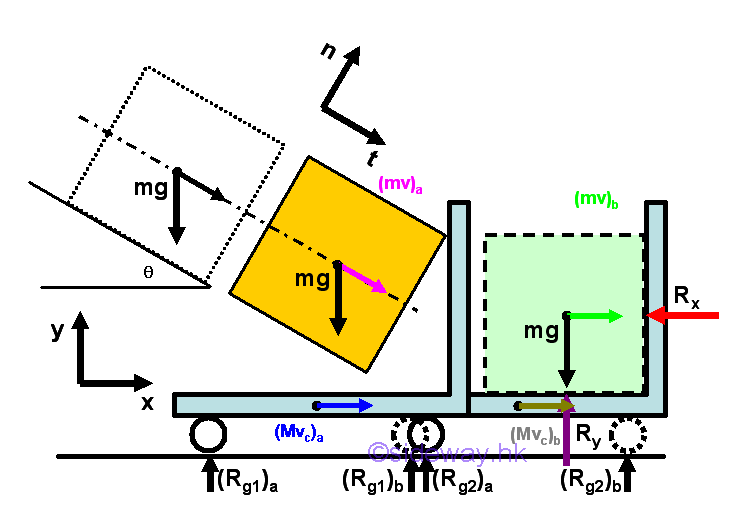
When an sliding object falls from the frictionless inclined surface onto a moving cart, the motion of the falling object produces an impulse acting on the cart. Since the cart also exerts forces on the object, the object finally come to rest on the cart and move together with the cart at the same velocity.
Considering the object and cart as a system, the velocity components along x direction can be obtained by the principle of impulse and momentum. Since there is no external force along x direction, imply
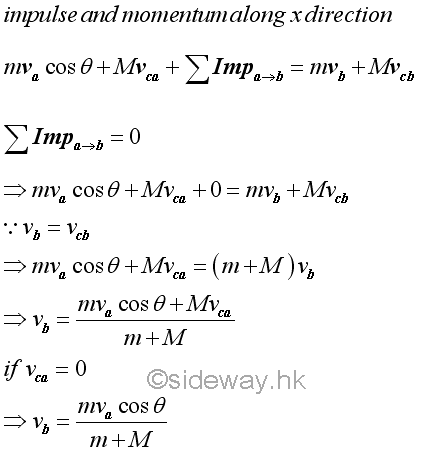
Since both the initial and final velocities of the object are known, the impulses act upon the object can be determined by the principle of impulse and momentum.
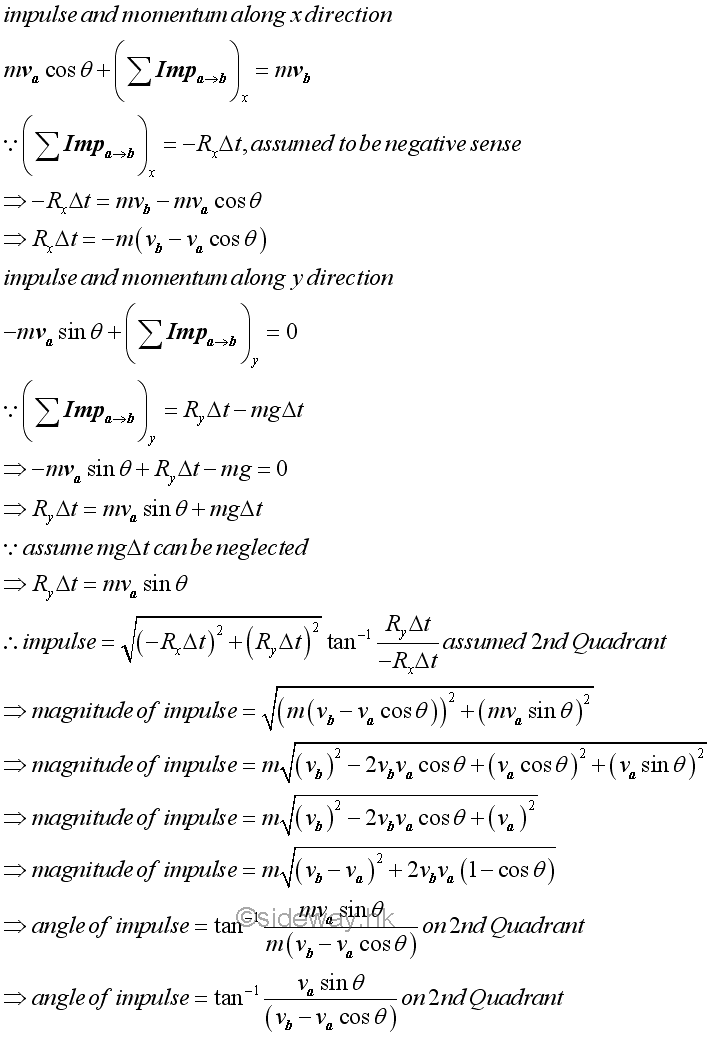
Since the motion of the cart is limited to along x direction only, part of the kinetic energy of the falling object is lost.
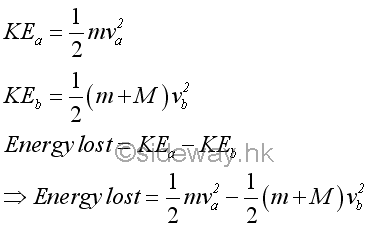
Impulses to Change the Direction of a Ball
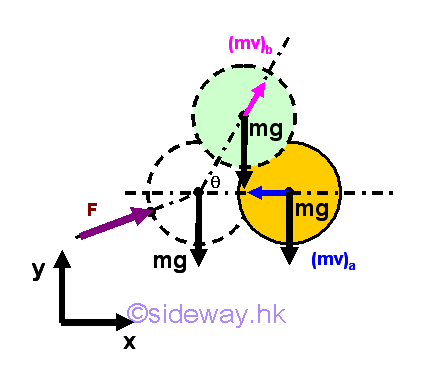
When an moving object is hit by a bat, the impulse produced by the bat can be expressed as an average impulsive force exerted on the object during the contact time t. Usually, the bat and the ball are in contact for a very short period time, e.g. 0.02second, the impulse due to the body force is much smaller than the applied force due to the bat and therefore the impulsive body force can be neglected. The momentum change of the object can be determined by the principle of impulse and momentum.

Impact and Momentum
Impact is a collision between two objects over a short time interval in which momentum changes of the two objects can be explained by the principle of impulse and momentum.
Impact of Two Free Objects
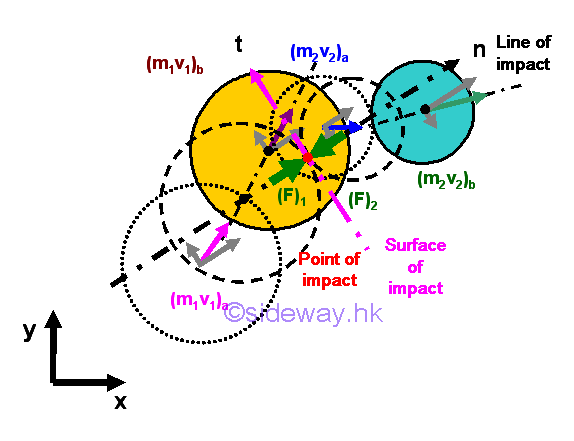
For two free objects, if the body forces acting upon the objects are neglected and there is no external force acting on the two objects, the total momentum of two objects is conserved.

If the contact surfaces of the two objects are perfectly smooth and frictionless, the line of impact is normal to the surface of impact and therefore the impulsive force is always along with the line of impact also. By the principle of impulse and momentum, the momentum changes of the two objects can be resolved into components tangential and normal to the surface of impact.

By the concept of impact, two objects are first deformed at the beginning of the collision and then two objects will be restored after the point of kinetic equilibrium at which two objects move at same velocity along the line of impact. The impulsive forces acting between two objects are therefore divided into the deformation period and the restoration period. Depending on the structural and material property of the two objects, the ratio of the magnitudes of impulses for the two specified colliding objects corresponding to the restoration period and the deformation period respectively is defined as the coefficient of restitution, which can be expressed as the ratio of the relative velocity of the two objects after the impact and the relative velocity of the two objects before the impact.

Since the relative velocities of two objects before the impact and after the impact can be related by the coefficient of restitution, the equations of impact can be solved simultaneously.

Impact of Object on a Fixed Wall
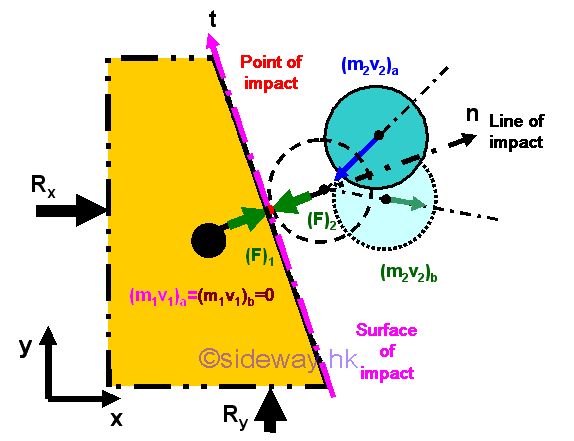
Considering a ball collides with a smooth frictionless fixed wall, there is no external force acting on the two objects, the total momentum of two objects is conserved. However the mass of the fixed wall connected to the earth is infinite, the equation of total momentum cannot be solved. But by the concept of impact, the relative velocities relationship related by the coefficient of resitution can still be applied. Since there is no friction between the ball and the wall, the line of impact must be normal to the surface of contact. The motion of the ball can therefore be resolved into tangential and normal components. As the infinite mass of the fixed wall much greater than the mass of the ball, the rebound velocity of the wall must approach zero inversely.
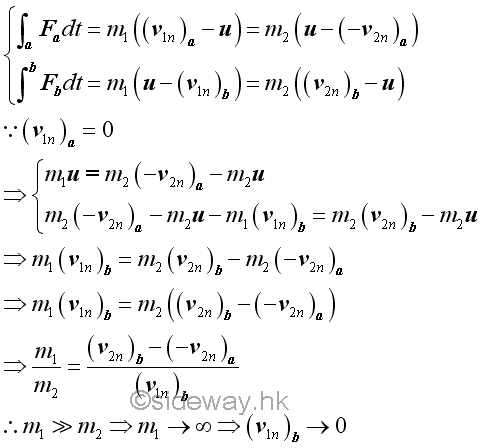
Imply
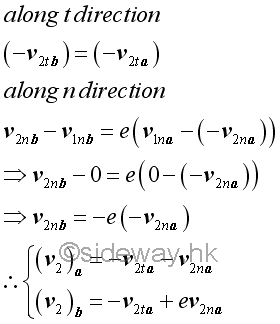
Or restricting to consider a finite frictionless fixed wall section of mass m with additional external reaction forces at the connections to react the impulsive forces acting on the wall at the point of impact such that the motion of the finite fixed wall section is equal to zero.
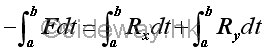
Since the velocity of the finite fixed wall section is always equal to zero, the velocity u of the impact at equilibrium must be equal to zero also. Therefore the velocity of the ball after impact can be determined by the equation of coefficient of restitution directly.
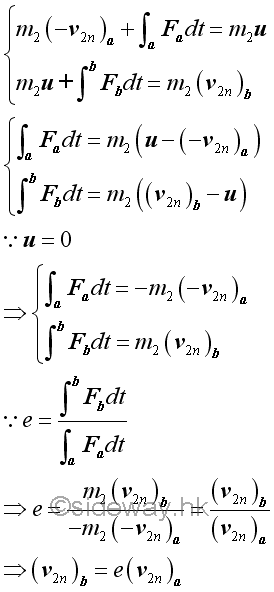
Impact of a ball on a Constrained Block
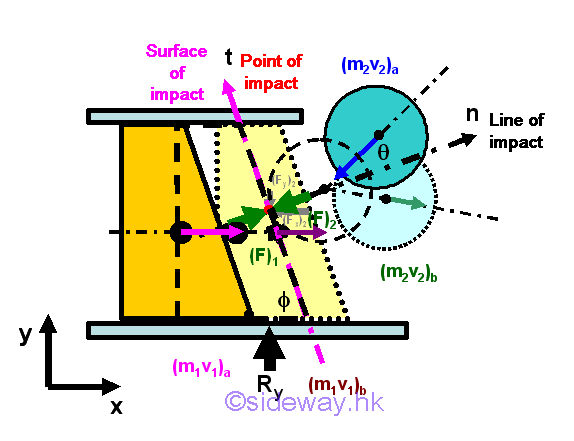
Considering a ball collides with a sliding block which moves in a smooth frictionless guide, if there is no friction between the ball and the block, the line of impact must be normal to the surface of contact. When the body weights of the ball and the block is neglected, the reaction force of the guide acting upon the block to react the block weight is neglected also. However there exists an external reaction impulsive force of the guide acting upon the block to react the impulsive force of the impact. The four unknowns after the impact is the impulsive force over the time interval in y direction, the horizontal velocity of the sliding block, the tangential and normal components of the velocity of the ball. The concepts of impulse and impact are used to relate the motion of two objects before and after the impact.
Since the vertical motion of the block along y direction is limited by the guide, the motion of the block is limited to horizontal motion along x direction only. By the principle of impulse and momentum, there is no external impulse along x direction, the total momentum of the block and the ball is conserved along x direction while the total momentum along y direction is not.
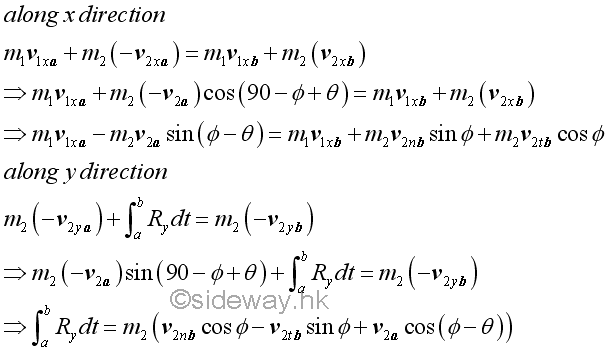
By the concept of impact, the coefficient of restitution expressed in terms of the relative velocityes of the block is

Similarly, the coefficient of restitution expressed in terms of the relative velocityes of the ball is

Therefore the coefficient of restitution is
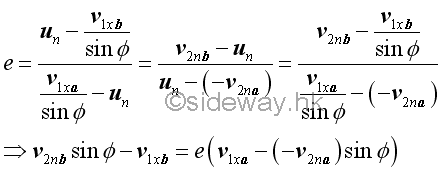
The equations of impacts are

©sideway
ID: 141200005 Last Updated: 1/1/2015 Revision: 1 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
