Content
Kinetics: Kinetic Motions of System of Particles
Equipollent System of Overall Force
Overall Force of A System of Particles
Overall
Moment of A System of Particles
Effective Forces of A System of Particles
Kinetic Motion of a System of Particles
Overall
Linear Momentum of A System of Particles
Overall Angular Momentum of A System of Particles
Overall
Rate of Change of Motion of A System of Particles
Motion
of Mass Center of a System of Particles
Mass Center of a System of Particles
The Rate of Changes for the Motion of Mass Center of a System of Particles
Motion of a System of Particles about Mass Center of the System of Particles
Kinematics of a System of Particles
Overall Momentum of a System of Particles about Mass Center
Overall Force of a System of Particles about Mass Center
Overall Angular Momentum of a System of Particles about Mass Center
Overall Moment of a System of Particles about Mass Center
Conservation of Momentum for System of Particles
Convservation of Momentum of System of Particles about Fixed Point
Convservation of Momentum of Mass Center about Fixed Point
Convservation of Momentum of System of Particles about Mass Center
Kinetics: Kinetic Motions of System of Particles
When considering a system of n particles, n coupled equations of motion can be derived for each individual particle using Newton's second law as used in particle objects. But this is not an easy task if the number of particles n tends to a very large value. However the study can also be focused on the overall motion of a system of particles instead of the detailed motion of each individual particles.
Equipollent System of Overall Force
For a system with n particles, let individual particle pi of mass mi, with position ri, and acceleration ai, where 1≤i≤n, be particles of the system with reference to a newtonian frame of reference. The overall force acting on the system of particles is the initial cause for the motion of the system of particles.
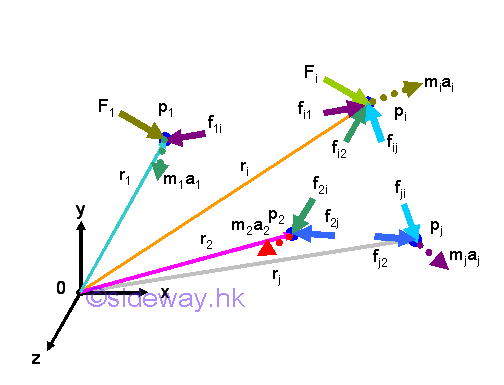
Overall Force of A System of Particles
Since there are more than one particle object in the system, forces acting upon an object pi can be an internal force fij, exerted by another particle pj of the system and an resultant external force Fi of all the external forces acting on the particle pi. Internal force fij, is the force acting on the ith particle due to the iteraction with the jth particle, where 1≤i≤n and 1≤j≤n. By Newton's third law, an internal force fij is equal to the negative sense of the corresponding internal force fji. And internal force acting on itself must be equal to zero because there is no interaction, fij=fii=0 when j=i. By Newton's second law, the dynamic equilibrium equation in terms of forces for the ith particle is
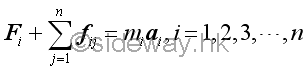
The overall force of a system of particles can therefore be obtained by adding all the n force equations of the particles in the system.
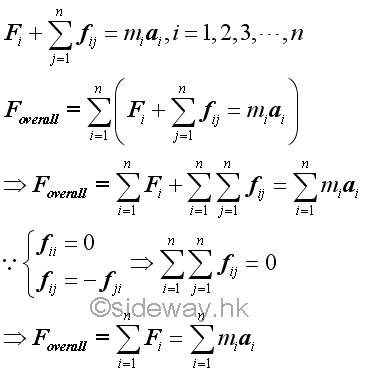
Overall Moment of A System of Particles
The moment of every particle in the system of with respect to the origin O can also be obtained by taking the moments about O of all forces acting upon a particle in the system. The dynamic equilibrium equation in terms of moment for the ith particle is
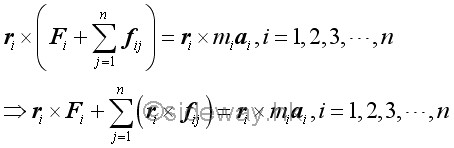
The overall moment of a system of particles can therefore be obtained by adding all the n moment equations of the particles in the system.
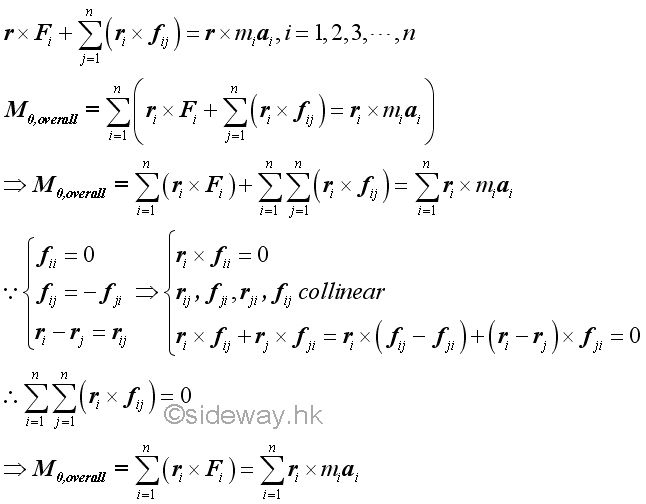
Effective Forces of A System of Particles
Both the resultant force of all the internal forces of the system and the resultant moment of the moments of all internal force of the system are equal to zero, the overall motion of the system of particles is only due to the system of the external forces. The kinetic motions of the system of particles are called the effective forces, i.e. miai. Since the system of the external forces acting on the system of particles and the system of the effective forces of the system of particles have the same resultant force and same resultant moment, the two systems of forces are equipollent.
Although the resultant force of the internal forces of a system of particles is equal to zero, the effects of internal forces acting upon the particles of the system are still one of the primary causes for the motion of the system of particles.
Similary, two systems of external forces with the same overall force and overall moment may not have the same effect on a given system of particles because both the internal forces and the effects on the motion of the system of particles will change with respect to the external forces acting on each individual particle in the system.
Kinetic Motion of a System of Particles
The overall force and overall moment of a system of particles cause an overall acceleration and angular acceleration about 0 on the system of particles. By Newton's first law, the state of the motion of a particle in the system is therefore changed by the force acting on the particle.
Overall Linear Momentum of A System of Particles
The overall momentum of a system of particles can be obtained by adding all linear momentum of the system of particles. Let vi be the velocity of the ith particle. The momentum pi of the ith particle is equal to the product of mivi.
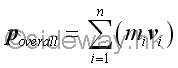
Overall Angular Momentum of A System of Particles
Similarly the overall angular momentum of a system of particles can be obtained by adding all angular momentum of the system of particles. Let vi be the velocity of the ith particle. The angular momentum Li of the ith particle is equal to the product of rixmivi.
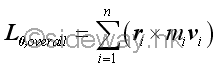
Overall Rate of Change of Motion of A System of Particles
The overall rate of change of the motion of a system of particles can be obtained by differentiation the linear momentum and angular momentum of the system of particles.
Similar to the motion of an object, the rate of change of the overall linear motion of a system of particles is equal to the overall external force of the system of particles.
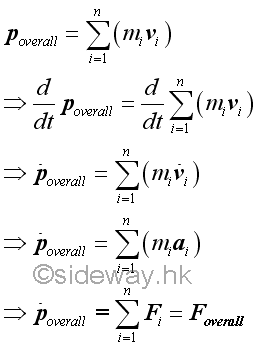
Similar to the motion of an object, the rate of change of the overall angular motion of a system of particles about 0 is equal to the overall moment of the system of particles about 0.
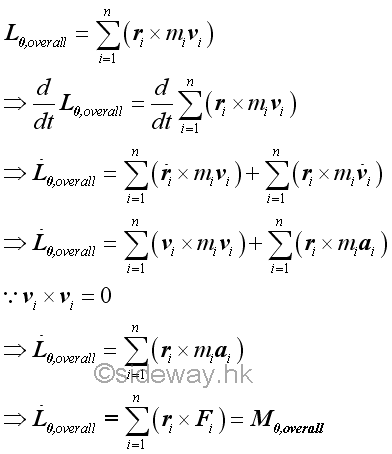
Motion of Mass Center of a System of Particles
Similar to the idealization of an object as a particle, the overall force of the system of particles can also be expressed in terms of the mass center of the system of particles.
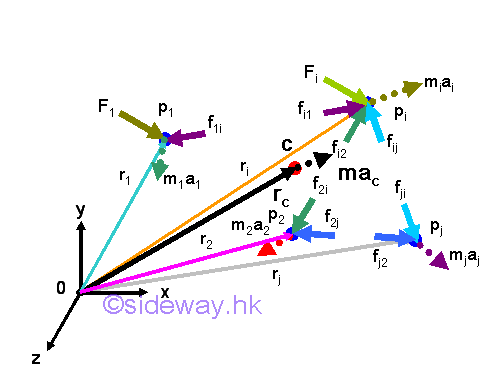
Mass Center of a System of Particles
For a system of moving particles at every instant in time, there is a unique location in space which is the average position of the mass of the system of particles. By definition, the mass center of the system of particles is the point at the position rc, at which the product of the total mass and the position vector of mass center is equal to the sum of the mass of every particle multiply by the corresponding position vector for a discrete system.

The Rate of Changes for the Motion of Mass Center of a System of Particles
Velocity of the mass center, the rate of change of the position of the mass center, of a system of particles can be obtained by differentiation the position vector of the mass center of the system of particles. Acceleration of the mass center, the rate of change of the velocity of the mass center, of a system of particles can be obtained by differentiation the velocity vector of the mass center of the system of particles.
Similar to the motion of an object, the rate of change of the product of total mass and position of the mass center of a system of particles is equal to the overall momentum of the system of particles.
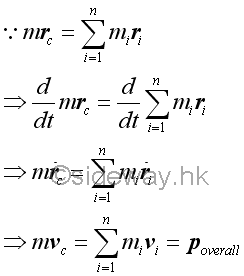
Similar to the motion of an object, the rate of change of the linear motion of the mass center of a system of particles is equal to the overall external force of the system of particles.
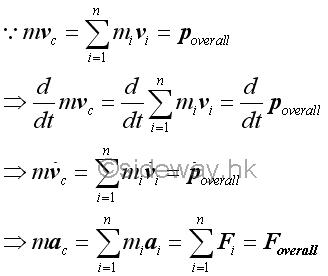
The center of mass and center of gravity can only be used synonymously in a uniform gravity field. Since the gravitation forces acting upon a system of particles are alway pointed toward the center of the Earth, in general the mass center and the center of gravity of a system of particles do not coincide exacly.
From the equation of linear motion for the mass center of a system of particles, the acceleration of the total mass of the system of particles at the mass center is equal to the effective forces of the system of particles. And therefore the acceleration of the mass center is only affect by the external forces, while the internal forces do not affect the motion of the mass center of a system of particles. This is because the internal forces are assumed always pair-wise forces of equal in magnitude and opposite in direction. For example, the motion of an exploding object due to an impulsive internal explosion. In other words, if the external force is equal to zero, the momentum of the mass center of a system of particles is always equal to the sum of the momentum of all particles in the system due to the internal forces at any instant. Or the product of total mass and position of the mass center of a system of particles is always equal to the sum of the product of mass and position of every particle in the system as in deriving the mass center of a system of particles.
Similar to the motion of an object, the rate of change of the overall angular motion of the mass center of a system of particles about 0 is not equal to the overall moment of the system of particles about 0.
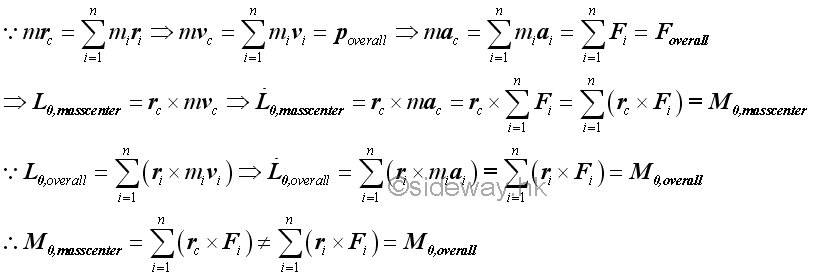
Although the acceleration of the total mass of the system of particles at the mass center is equal to the effective forces of the system of particles or the overall external forces, in general, the moment of effective forces at the mass center about 0 is not equal to the overall moment of the system of particles about 0. The overall external forces acting upon a system of particle and the equivalent force vector in terms of the acceleration of the total mass of the system acting upon the mass center of the system of particle are not equipollent.
Motion of a System of Particles about Mass Center of the System of Particles
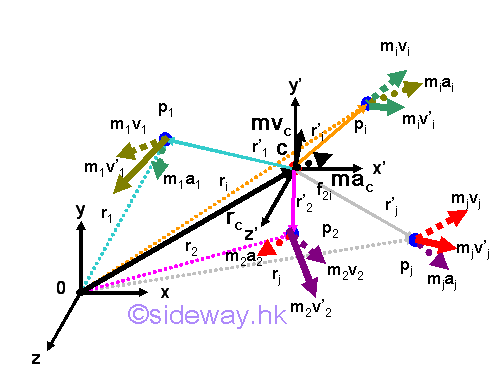
Sometimes the motion of a system of particles is more convenient to be considered with respect to the mass center of the system of particles. When a system of particles moves in space, the mass center of the system of particles also moves accordingly. Therefore a centroidal frame of reference C, in general, is not a newtonian frame of reference, moving in accordance with Newton's first law at most with constant velocity with respect to other Newtonian frames of reference 0. However, at any instant of time, the kinetic motion of the system of particles must hold for any frame of reference as the motion of the system must be in dynamic equilibrium. For example, kinetic motion with respect to frame 0 implies kinetic motion also holds with respect to frame C. The kinetic motion of a system of particles with respect to the moving centroidal frame of reference C can be expressed in standard form accordingly.
Kinematics of a System of Particles
The kinematics of the system of particles with respect to the translated frame C are
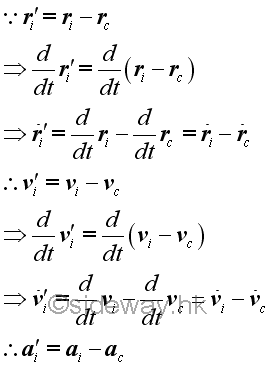
For a discrete system, the sum of the mass of every particle multiply by the corresponding position vector with respect to the mass center of the system of particles must always be equal to zero.
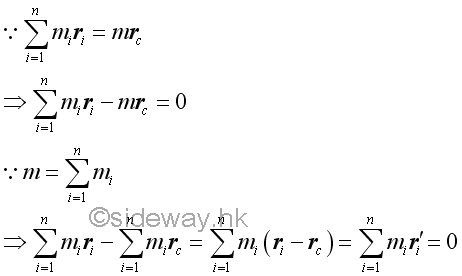
Overall Momentum of a System of Particles about Mass Center
For the overall momentum of a system of particles with respect to the mass center of the system of particles, the overall momentum with respect to the mass center of the system of particles is changed because the velocity with respect to the moving frame C is different from the velocity with respect to the Newtonian frame of reference 0.

Overall Force of a System of Particles about Mass Center
Although the sum of external forces acts on the system of particles is not changed with respect to the moving frame 0, the overall effective force with respect to the mass center of the system of particles is also changed because the relative acceleration with respect to the moving frame C is different from the relative acceleration with respect to the Newtonian frame of reference 0. In other words, the sum of external forces acts on the system of particles is changed with respect to the moving frame C.

Overall Angular Momentum of a System of Particles about Mass Center
For the overall angular momentum of a system of particles with respect to the mass center of the system of particles, the overall angular momentum with respect to the mass center of the system of particles is changed because the velocity with respect to the moving frame C is different from the velocity with respect to the Newtonian frame of reference 0.
However, since the sum of the mass of every particle multiply by the corresponding position vector with respect to the mass center of the system of particles must always be equal to zero equal vector at the mass center of the system of particles, the angular momentums of a system of particles with respect to the moving frame C due to the velocities with respect to the moving frame of reference C and the velocities with respect to the Newtonian frame of reference 0 must be the same.
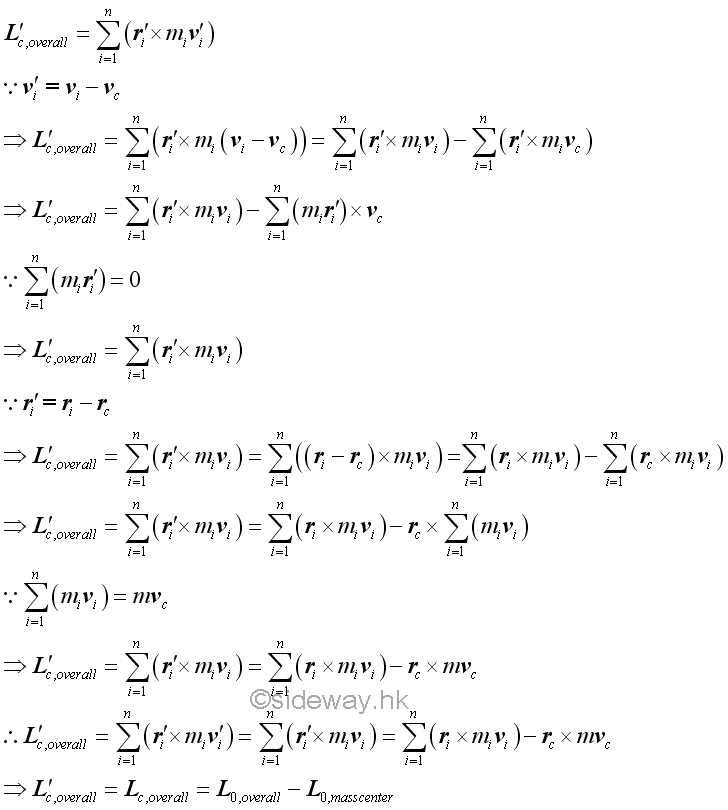
But, the angular momentums of a system of particles with respect to the Newtonian frame 0 due to the velocities with respect to the moving frame of reference C and the velocities with respect to the Newtonian frame of reference 0 are not the same.
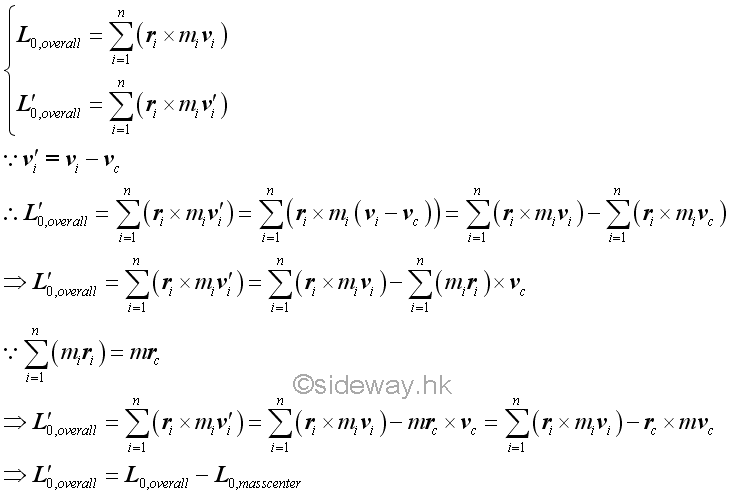
That is.
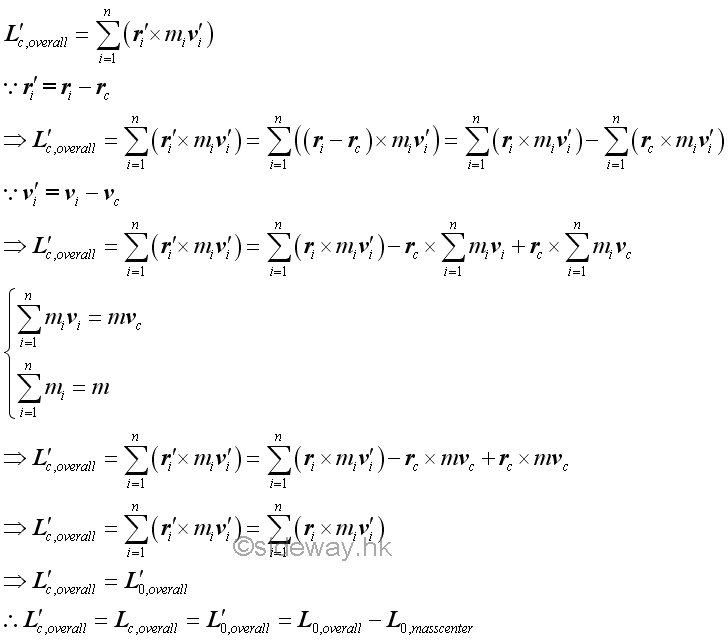
Overall Moment of a System of Particles about Mass Center
For the overall moment of a system of particles with respect to the mass center of the system of particles, the overall moment with respect to the mass center of the system of particles is changed because the acceleration with respect to the moving frame C is different from the acceleration with respect to the Newtonian frame of reference 0.
However, since the sum of the mass of every particle multiply by the corresponding position vector with respect to the mass center of the system of particles must always be equal to zero equal vector at the mass center of the system of particles, the overall moment of a system of particles with respect to the moving frame C due to the accelerations with respect to the moving frame of reference C and the accelerations with respect to the Newtonian frame of reference 0 must be the same.
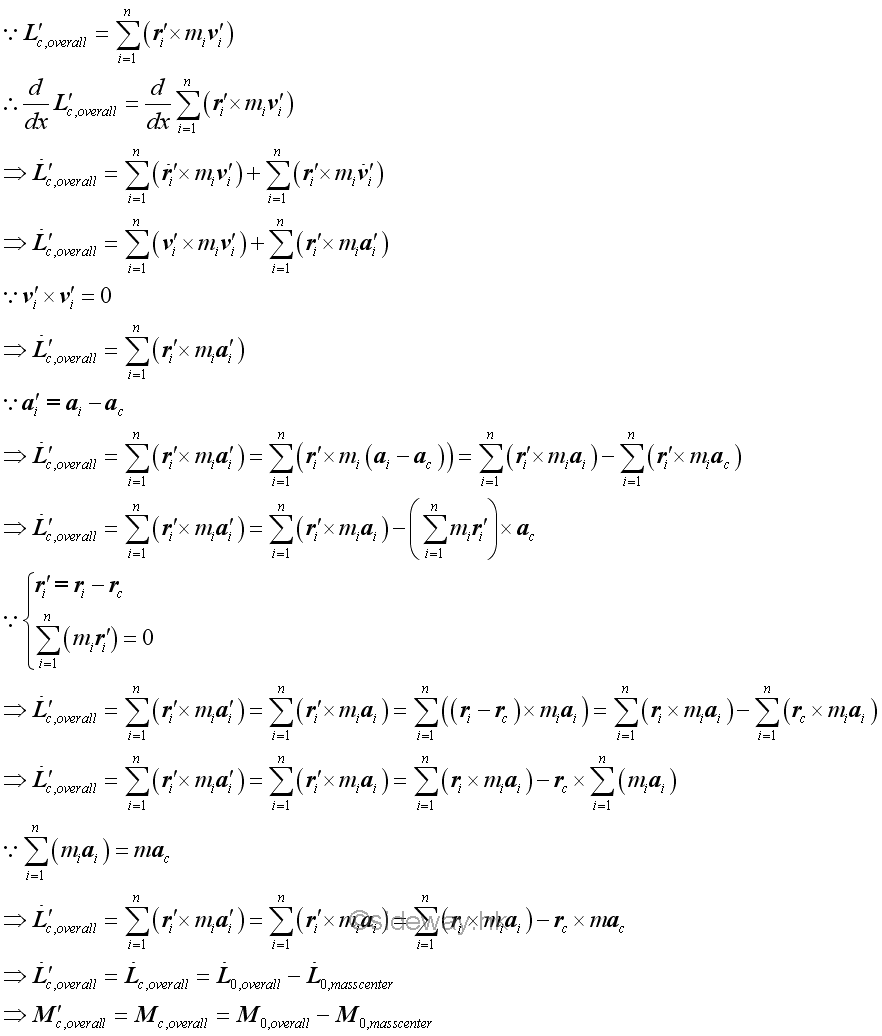
That is.
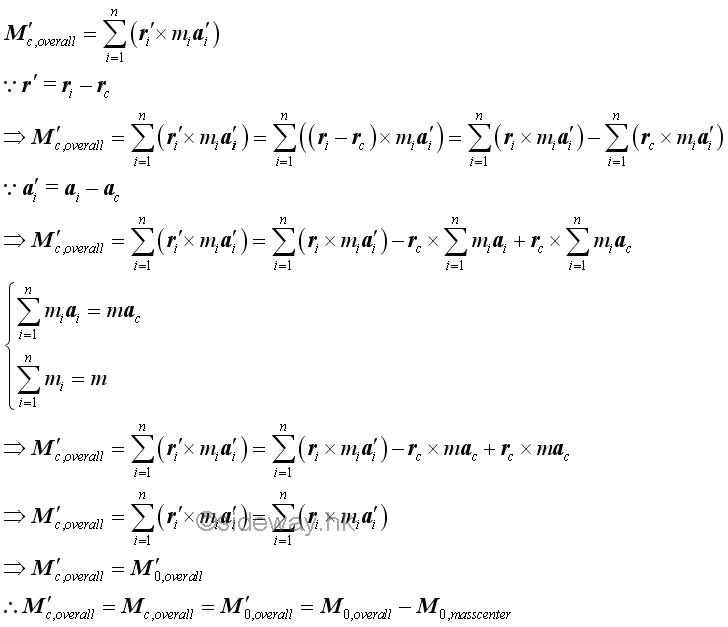
Conservation of Momentum for System of Particles
Convservation of Momentum of System of Particles about Fixed Point
When there is no external force acts upon a system of particles, the overall force acts on the particles of a system must be equal to zero. Since the internal forces act upon the particles of a system may not be equal to zero, the effective force of an individual particle is not equal to zero. However, the sum of the effective forces of the system of particles must be equal to zero also. If no external force acts on the particles of the system, the rate of change of the overall or sum of the linear momentum of the system of particles must be equal to zero. In other words, the overall or sum of the linear momentum of the system of particles must alway be equal to a constant with respect to time. Imply
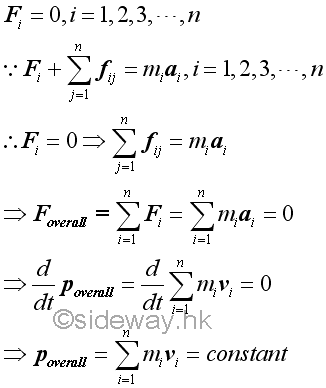
Similarly, when there is no external force acts upon a system of particles, the overall moment of the particles of a system must be equal to zero. Since the internal forces act upon the particles of a system may not be equal to zero, the effective moment of an individual particle is not equal to zero. However, the sum of the effective moment of the system of particles must be equal to zero also. If no external force acts on the particles of the system, the rate of change of the overall or sum of the angular momentum of the system of particles must be equal to zero. In other words, the overall or sum of the angular momentum of the system of particles must alway be equal to a constant with respect to time. Imply
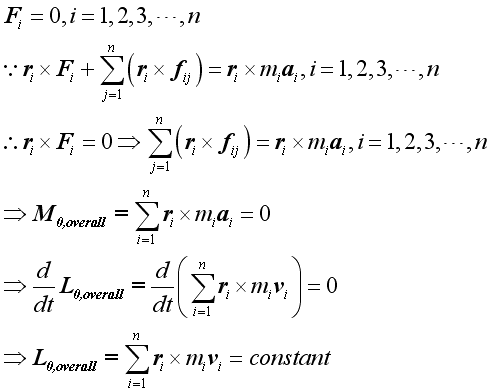
Therefore if there is no external force acts on particles of a system, both the overall linear momentum of the system of particles and the overall angular momentum of the system of particles about a fixed point 0 are conserved.
However, the overall angular momentum of a system of particles about a fixed point 0 can also be conserved, if not all external force acts on the particles of a system is equal zero. For example, the moment of a system of particles under central forces about a fixed point 0 is always equal to zero while the forces act upon the particles of the system are always not equal to zero. And since the moment of particles of a system is always equal to zero, the angular momentum of the system of particles about the fixed point must be constant.
Convservation of Momentum of Mass Center about Fixed Point
If there is no external force acts on particles of a system, both the overall force of the system of particle and the overall force acts on the mass center must be equal to zero. And therefore the acceleration of the mass center is also equal to zero. In other words, the mass center of the system of particles moves in a straight line with constant speed. Therefore the linear momentum of the mass center must be constant.
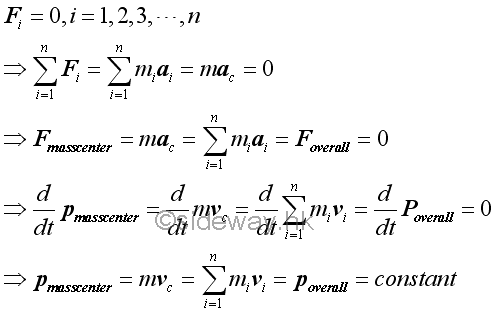
Similarly, if there is no external force acts on particles of a system, the angular momentums of external forces of the system of particles act on the mass center of the system of particles about a fixed point 0 is equal to zero. Therefore the angular momentum of the mass center about the fixed point 0 must be constant.
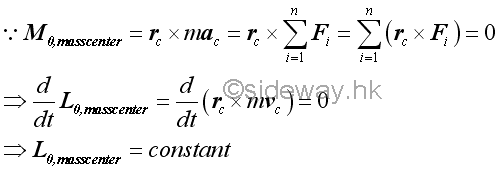
Therefore, if there is no external force acts on particles of a system, both the overall linear momentum of the system of particles and the overall angular momentum of the system of particles about a fixed point 0 are conserved.
Convservation of Momentum of System of Particles about Mass Center
Since the overall force of the system of particles with respect to the moving frame C is always equal to zero, the overall or sum of the linear momentum of the system of particles must alway be equal to a constant with respect to time. Imply
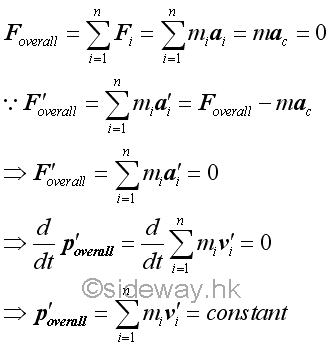
Similarly, when there is no external force acts upon a system of particles, the overall angular moment of the particles of a system and the overall angular moment of the mass center must be equal to zero about fixed frame 0. Therefore the overall angular moment of a system of particles with respect to the moving frame C due to the velocities with respect to the moving frame of reference C and the velocities with respect to the Newtonian frame of reference 0 must be the same and are equal to zero. In other words, the corresponding overall or sum of the angular momentum of the system of particles must alway be equal to a constant with respect to time. Imply

Therefore if there is no external force acts on particles of a system, both the overall linear momentum of the system of particles and the overall angular momentum of the system of particles about a moving frame C are conserved.
©sideway
ID: 150100002 Last Updated: 1/14/2015 Revision: 1 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
