Content
Differentiation
Derivative of a function
Differentiation
Derivative
Higher
Derivative
Differentiation
Differentiation is concerned with the deriving of the derivative of a function.
Derivative of a function
In many daily life problems, knowing how a dependable variable changed with an independable variable is also very important.
For example a function f :
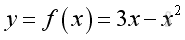
Graph of the function is
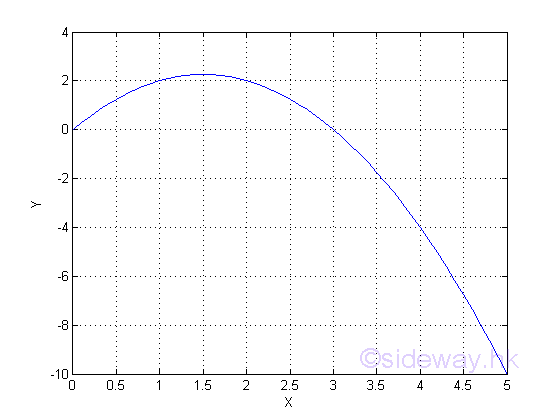
When x=1; y=2; and when x=2; y=2 also. And from the graph, the value of y increases then decreases as the value of x increases. The graph can only give a picture of the function and there is no information on how y vary with x
When considering a small change in the independence variable, there will be a small change in the dependence variable also. Let the small variation of variable x is Δx and the small variation of variable y is Δy. The calculated results of some small changes are:
| x=1 | 1.1 | 1.01 | 1.001 | 1.0001 | x=2 | 2.1 | 2.01 | 2.001 | 2.0001 |
| Δx=0 | 0.1 | 0.01 | 0.001 | 0.0001 | Δx=0 | 0.1 | 0.01 | 0.001 | 0.0001 |
| y=2 | 2.09 | 2.0099 | 2.000999 | 2.00009999 | y=2 | 1.89 | 1.9899 | 1.998999 | 1.99989999 |
| Δy=0 | 0.09 | 0.0099 | 0.000999 | 0.00009999 | Δy=0 | -0.11 | -0.0101 | -0.001001 | -0.00010001 |
| Δy/Δx=0/0 | 0.9 | 0.99 | 0.999 | 0.9999 | Δy/Δx=0/0 | -1.1 | -1.01 | -1.001 | -1.0001 |
From the table, the variation of Δy in relation to Δx is obtained. According to the calculated results, the value of Δy varies on both Δx and x. And the reduction of Δx can also reduce the value of Δy.
Therefore Δy/Δx is not a constant but a function of Δx and x. Since Δy/Δx is indeterminate when Δx=0 and the value of Δy is reduced as Δx becomes small, the variation of Δy/Δx as Δx approaching 0 can be evaluated by its limit. This type of limit is named derivative and the notation is:
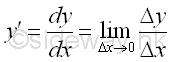
Or in the form of function f with number a be the element x of X:
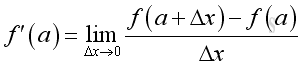
And from the table, the derivative of the function f at a, when a=1 and a=2 are as following:
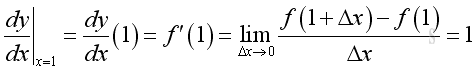
and
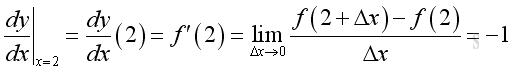
Although the value of y is equal to 2 when x=1 and x=2, the variation of Δy in relation to Δx at x=1 is increasing and equal to 1 while the variation of Δy in relation to Δx at x=2 is decreasing and equal to -1.
Differentiation
Instead of using a number a to find the value of the derivative of the function f at a, the Δy/Δx ratio can be expressed in the form of of Δx and x. Imply
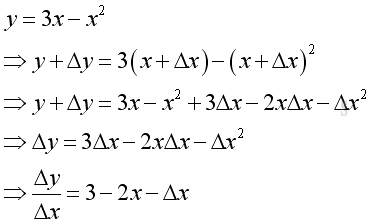
And the derivative of the function f is:
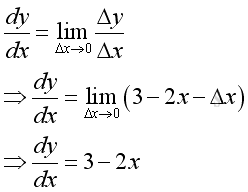
Therefore when Δx approaching 0, the derivative of the function f is a function of x only. And when x=1, dy/dx=1; and when x=2; dy/dx=-1 as before. From the derivative function, a more clear picture of how Δy in relation to Δx as a function of x is obtained.
Derivative
For a given function f, if the derivative of the function f at c exist, the function f is dfferentiable at c. A function can be differentiated if and only if the function is continuous, in other words, f(c) is defined and f(c) equals to the limit of f(x) when x approaching c. However, not all continuous function are differentiable because the derivative should be defined at c also.
Therefore for a function f that is defined on an open interval (a,b), the function f is dfferentiable on an open interval (a,b) if the function f is dfferentiable at every number c in (a,b). Imply the derivative f'(c) of a function f at c exist, that is the following limit exists:
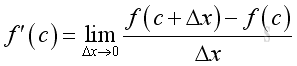
And for a function f that is defined on an closed interval [a,b], the function f is dfferentiable on an closed interval [a,b] if the function f is dfferentiable at every number c on the interior (a,b) and is differentiable from one side at its ends. Imply the derivative f'(c) of a function f at c exist and the following limits exists at the end points of the closed interval [a,b], that is:
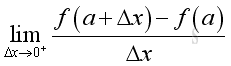 and
and
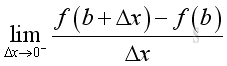
The deriviative of a function f is called the first derivative of the function f and is denoted by:
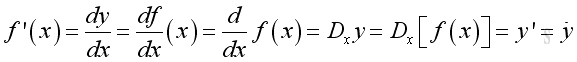
The deriviative of the derivative of a function f is called the second derivative of the function f and is denoted by:
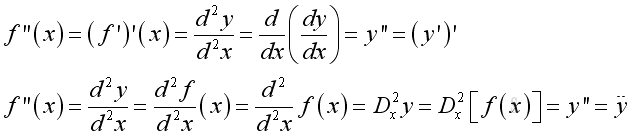
And the nth derivative of a function f can also be denoted in the similar way.
Higher Derivative
The deriviative of the derivative of the previous function f can be derived as following. The Δy'/Δx ratio of the first derivative of the function f can be expressed in the form of of Δx and x also. Imply
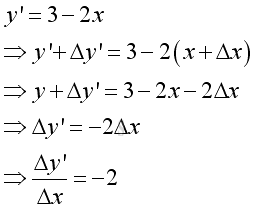
And the derivative of the derivative of the function f is:
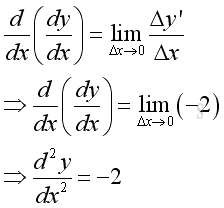
From the second derivative function, a very clear picture of how Δy' in relation to Δx is obtained.
Assumed the mentioned function f is the displacement as a function of time. Then the first derivative is the instantaneous velocity as a function of time. The second derivative is the instantaneous acceleration as a function of time.
And higher derivatives can be obtained by repeating the differentiation process , i.e. third derivative by taking the derivative of the second derivative... etc
©sideway
ID: 110900003 Last Updated: 9/20/2011 Revision: 1 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)
- Tefal BL83SD PerfectMix Cook Blender(last updated On 11/25/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/24/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/23/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/22/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
