Content
Rules of
Differentiation
Derivatives of Polynomials
Rules of Differentiation
In order to simplify the task of finding derivatives, some general rules are developed to help finding derivatives with having to use the defination directly.
Derivatives of Polynomials
-
Derivative of Constant Function
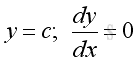
Proof:
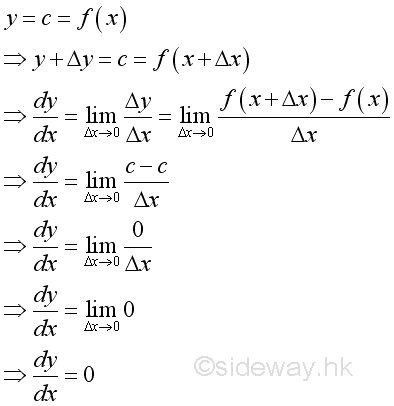
Derivative of Linear Function
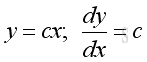
Proof:
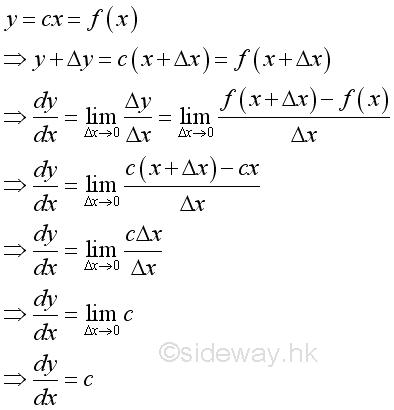
-
Derivative of Power Function
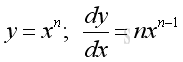
Proof when n is positive:
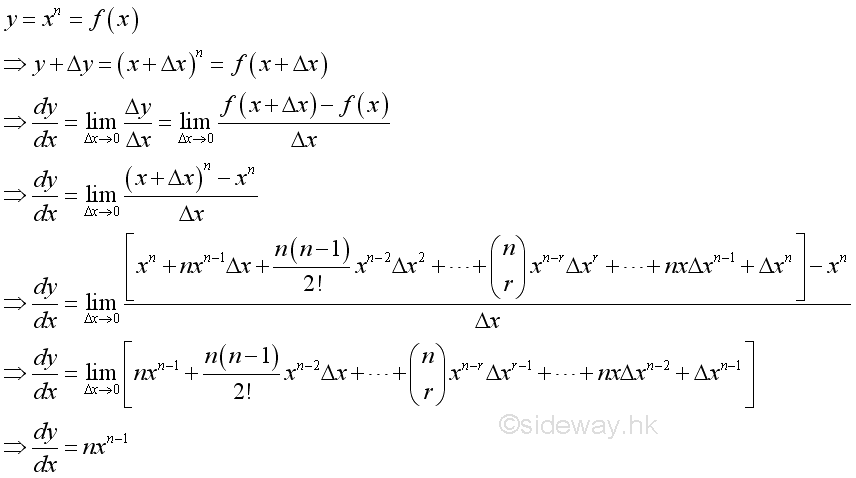
Proof when n is zero and x not equal to zero:
n can be any real number and proof will be included in the later part of rules.
Rule of Constant Multiple Function
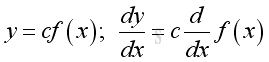
Proof:

Rule of Sum of Functions
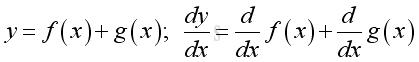
Proof:
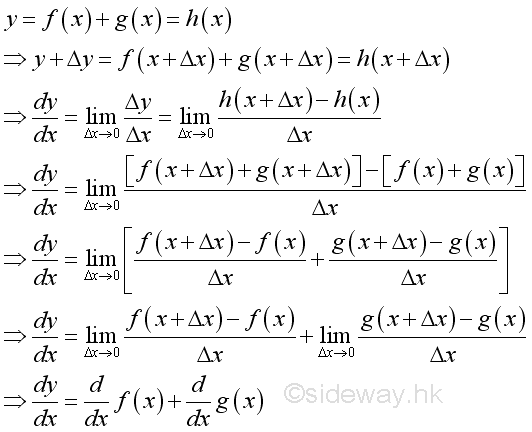
The sum of functions can be extended to the sum of any functions by repeating the sum rule.
Rule of Difference of Functions
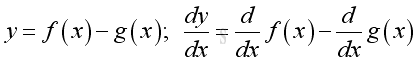
Proof if both functions are differentiable:
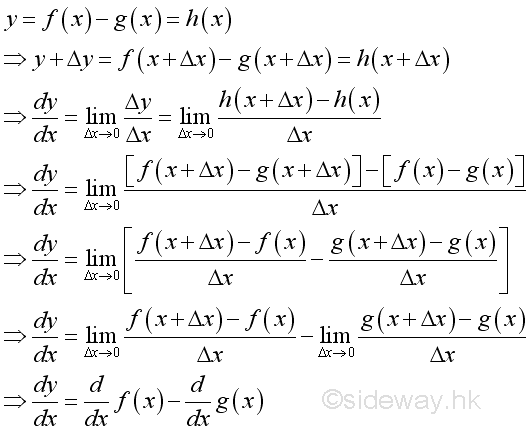
The difference of functions can be extended to the difference of any functions by repeating the difference rule. And the different rule can be obtained by applying the constant multiple rule to the sum rule.
Rule of Product of Functions
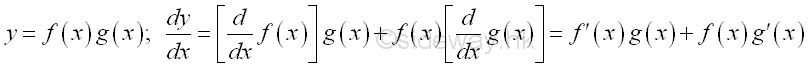
Proof if both functions are differentiable:
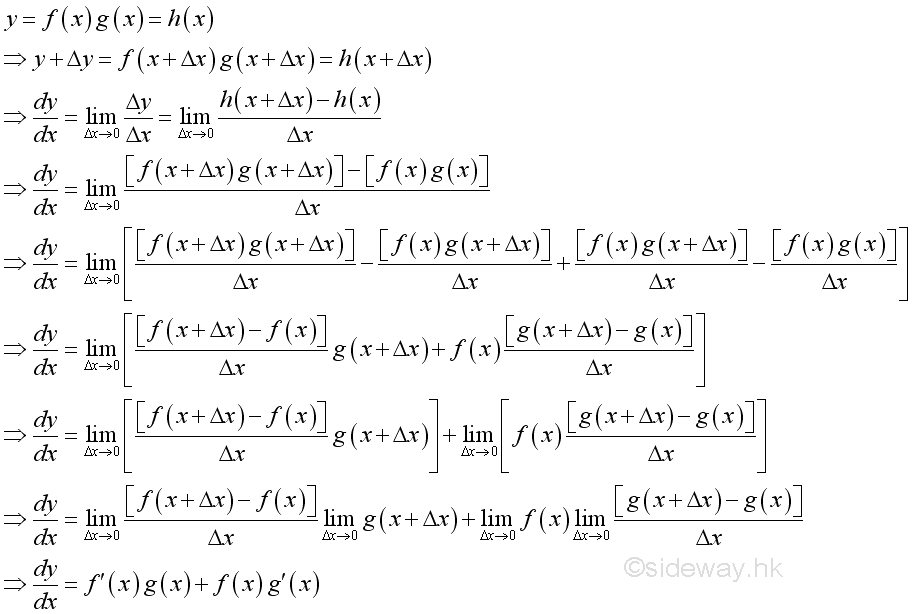
The proof is completed by subtracting and adding an addition expression in the numerator. Since both functions f and g are differentiable, they are continuous and f(x)=f(x+Δx) and g(x)=g(x+Δx) when Δx approaching zero. The product rule can also be extend to any number of functions.
Rule of Quotient of Functions
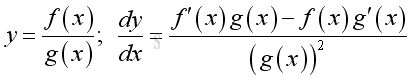
Proof if both functions are differentiable:

The proof is completed by subtracting and adding an addition expression in the numerator. Since function g is differentiable, it is continuous and g(x)=g(x+Δx) when Δx approaching zero.
Proof for the power function when n is negative:
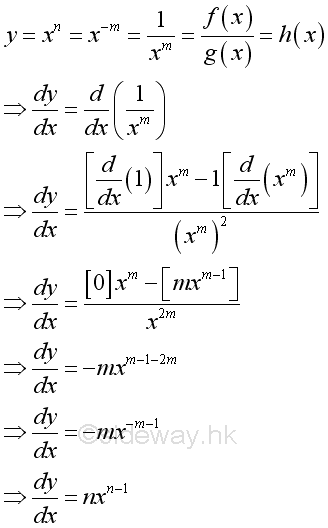
Rule of Composite Function (The chain rule):
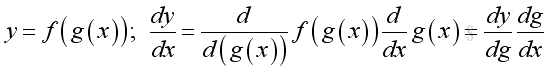
Proof if both functions are differentiable:
For g(x)
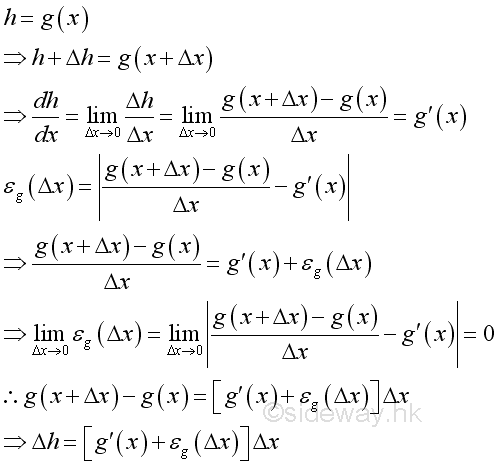
For f(g(x)):
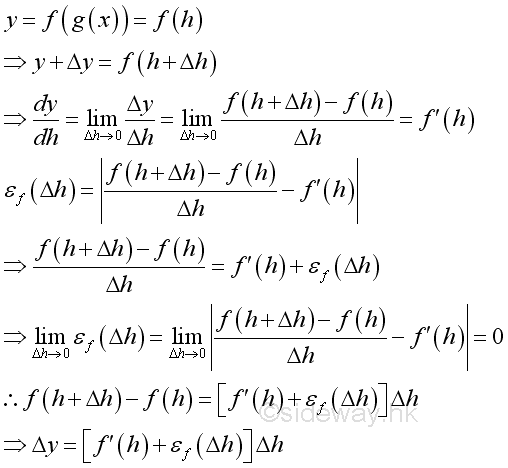
Therefore:

Since function g is differentiable, it is continuous. When Δx approaching zero, εg equals zero and Δh is approaching zero. And therefore εf equals zero as Δx approaching zero also. The rule of composite function can be extended to any number of composite function and the derivative can be expressed in form of a chain.
Rule of Inverse Function
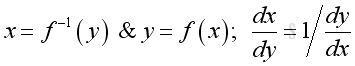
Proof if both functions are differentiable and x is the inverese function of y:
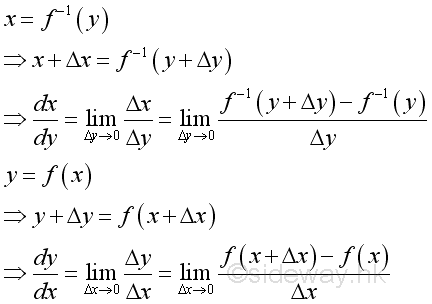
Since x=f-1(y) if and only if y=f(x):
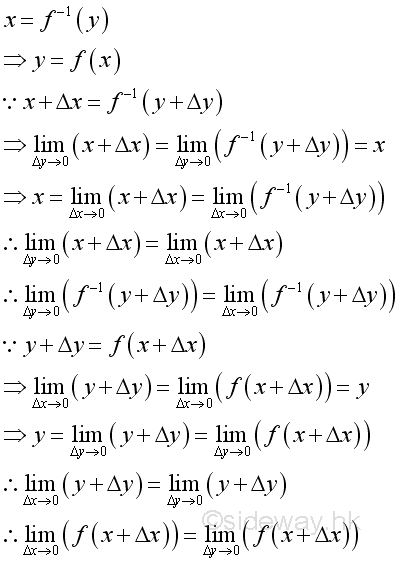
Therefore:
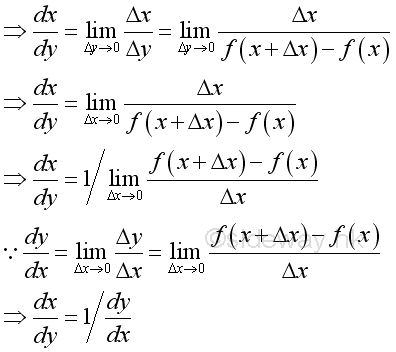
Proof for the power function when n is rational number:
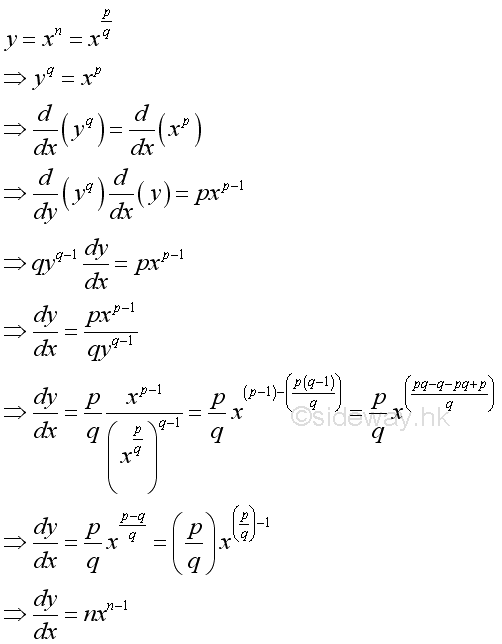
©sideway
ID: 110900005 Last Updated: 10/30/2011 Revision: 2 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Space(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 35
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
