Content
Derivatives of Inverse Hyperbolic Functions
Derivatives of
Inverse Hyperbolic Functions
Derivatives of Inverse Hyperbolic Functions
Inverse trigonometric functions are often found in physical applications.
Derivatives of Inverse Hyperbolic Functions
-
Derivative of Inverse Hyperbolic Sine Function
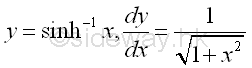
y is the value lying between -∞ and ∞ and x is the value of sinh y from -∞ to ∞. The slope of the curve is always positive, imply dy/dx is always positive.
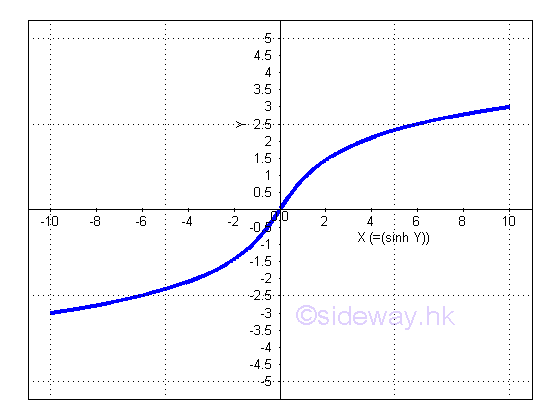
Proof:
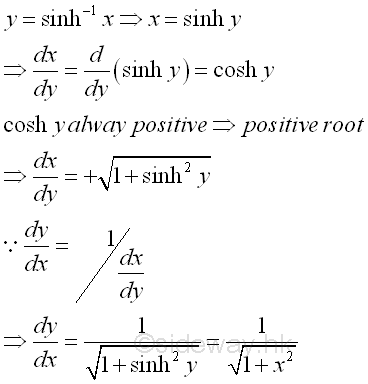
-
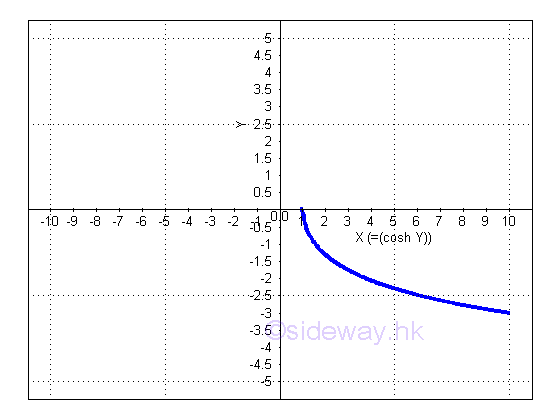
Derivative of Inverse Hyperbolic Cosine Function
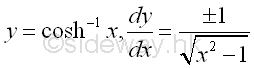
y is the value lying between 0 and ∞ or between 0 and -∞ and x is the value of sinh y from 1 to ∞. The slope of the curve is either always positive or always negative, imply dy/dx is either always positive or always negative.
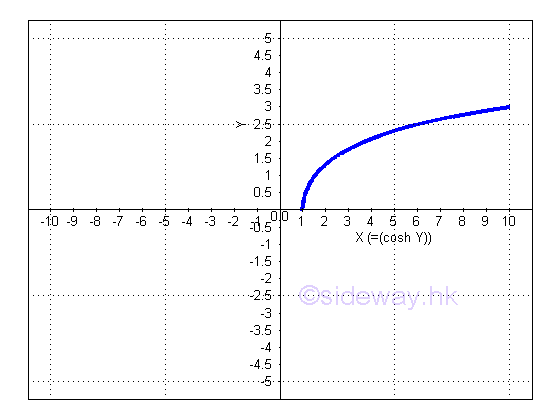 or
or
Proof:
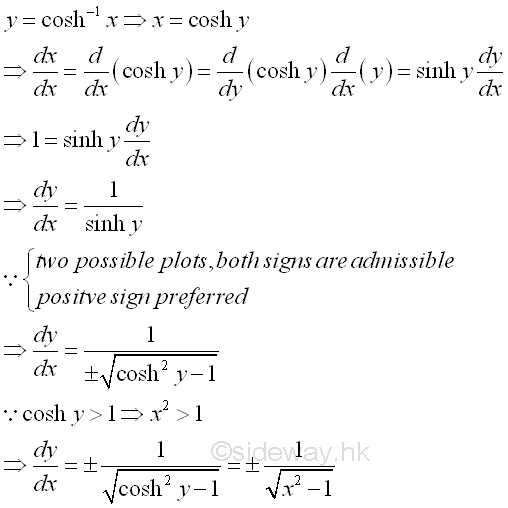
-
Derivative of Inverse Hyperbolic Tangent Function
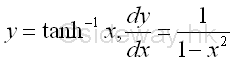
y is the value lying between -∞ and ∞ and x is the value of sinh y from -1 to 1. The slope of the curve is always positive, imply dy/dx is always positive.
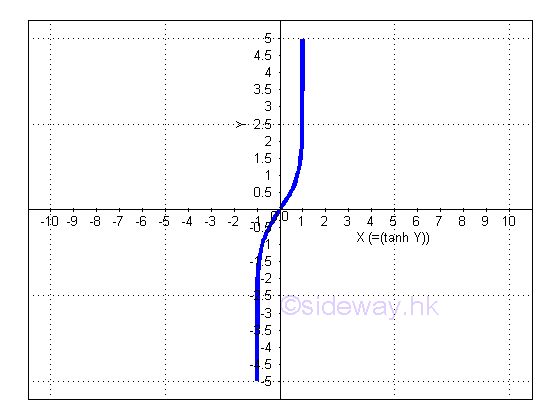
Proof:
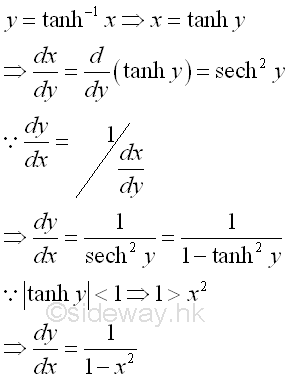
-
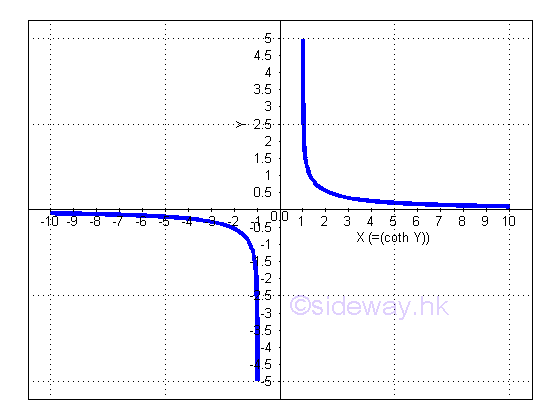
Derivative of Inverse Hyperbolic Cotangent Function
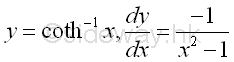
y is the value lying between -∞ and ∞ and x is the value of sinh y from -1 to ∞ and 1 to ∞. The slope of the curve is always negative, imply dy/dx is always negative.
Proof:
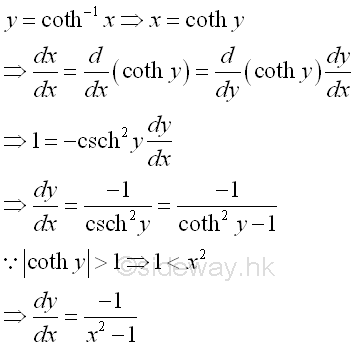
-
Derivative of Inverse Hyperbolic Secant Function
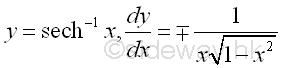
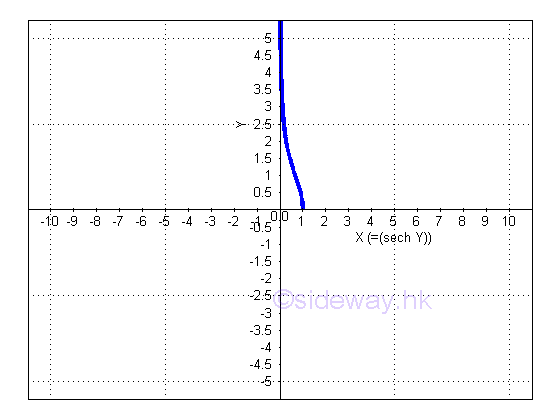
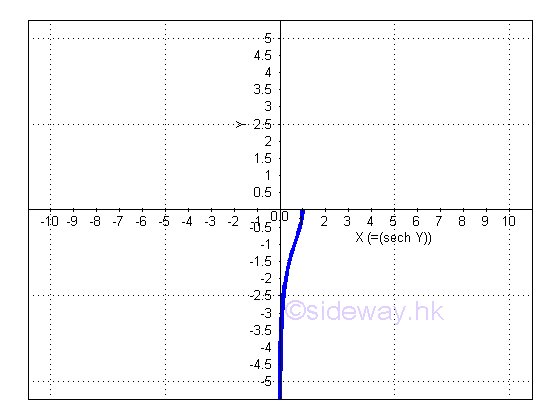
y is the value lying between 0 and ∞ or between 0 and -∞ and x is the value of sinh y from 0 to 1. The slope of the curve is either always positive or always negative, imply dy/dx is either always positive or always negative.
 or
or
Proof:

-
Derivative of Inverse Hyperbolic Cosecant Function
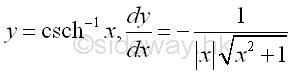
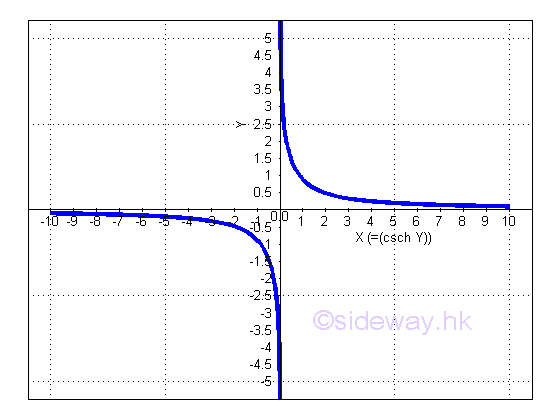
y is the value lying between -∞ and ∞ and x is the value of sinh y from -∞ to -1 and 1 to ∞. The slope of the curve is always negative, imply dy/dx is always negative.
Proof:
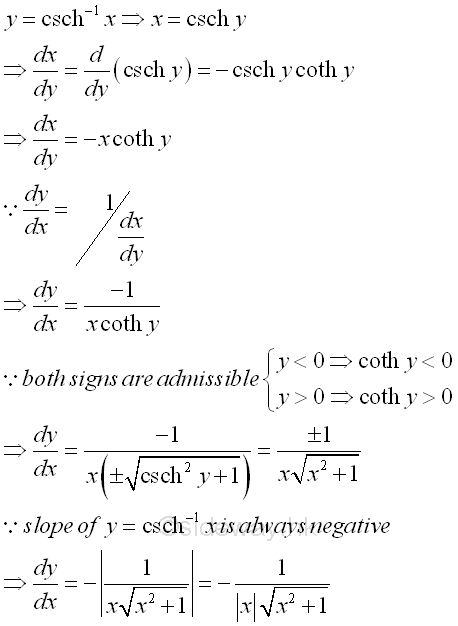
©sideway
ID: 130700018 Last Updated: 7/9/2013 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)
- Tefal BL83SD PerfectMix Cook Blender(last updated On 11/25/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/24/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/23/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/22/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
