Content
Prime Number
Prime Number
Factorization
Primality
Divisibility
Last Digit
Cyclisity
Greatest Common Divisior (GCD)
Euclidean algorithm
Bezout's Identity
Least Common Multiple (LCM)
Modular Arithmetic
Prime Number
Prime Number
Prime numbers are natural numbers, e.g. 2, 3, 5, 7,..., which can only be divided by 1 and itself. For other natural numbers, neither 1 nor prime number, they are called composite numbers. In general, a composite number can be expressed as a product of two factors, i.e. n=xy. 1 is not a prime because 1 can only be divided by 1 and 1 has one divisor, 1 only. Besides, prime numbers are always positive numbers. And 1 and 0 is neither prime nor composite.
There are infinitely prime numbers. 2 is one of most oddest prime number. 2 is the only even prime number because any even number greater than 2 is divisible by 2. 2 is also the smallest prime number. Similarly, 5 is the only prime number ends in 5 because any number end in 5 is divisible by 5. There is no prime number ends in 0 because any number ends in 0 is divisible by 2 and 5. Therefore, except 2 and 5, all prime numbers end in 1, 3,7, or 9. And all prime numbers above 3 can be expressed in the form 6n-1 or 6n+1.
Factorization
Any non-zero natural number, n can be factored into primes and expressed as a product of primes and powers of primes, n=xy=apbqcr. where n, x, y, p,. q, and r are natural numbers, and a, b, and c are prime numbers. The powers p, q, and r must greater or equal to one. Since all facors of an integer are primes, the factorization is call prime factorization. The prime factorization of an integer is unique except for the ordering of the factors.
Primality
Since a prime number, p can only be divided by 1 and itself, one of the method to verify the primality of a integer number, p is by trial division. For a composite number, the integer number n can be factored into two numbers, one of the possible factor is therefore must be less or equal to the square root of n, √n. And for an integer n greater than 1, there is always a prime number p such that n<p<2n.
Divisibility
The divisibility of an integer number for some integers can be examined by some rules:
-
2 - number with the last digit is even
-
3 - number with the sum of digits is divisible by 3
-
4 - number with the number of the last two digits is divisible by 4
-
5 - number with the last digit is 5 or 0
-
6 - number is divisible by both 2 and 3
-
7 - number with the number without the last digit minus the double of the last digit is equal to 0 or divisible by 7
-
8 - number with the number of the last three digits is divisible by 8
-
9 - number with the sum of digits is divisible by 9
-
10 - number with the last digit is 0
-
11 - number with the sum of every second digit minus the sum of other digits is equal to 0 or divisible by 11
-
12 - number is divisible by both 3 and 4
-
25 - number with the number of the last two digit is 00, 25, 50, or 75
Last Digit
The last n digits of the product of integers is equal to the last n digits of the product of last n digits of the integers. And the last digit of the n power of an integer is equal to the n power of the last digit.
Cyclisity
The cyclisity of the last digit in the integer power, greater than 0, of an integer with the last digit:
-
.0, 1, 5, 6 - the last digit in the integer power of an integer is same as the integer.
-
2, 3, 7, 8 - the cyclisity is equal to 4
-
2 - the last digit in the integer power of an integer is 2, 4, 8, 6, 2, ...
-
3 - the last digit in the integer power of an integer is 3, 9, 7, 1, 3, ...
-
7 - the last digit in the integer power of an integer is 7, 9, 3, 1, 7, ...
-
8 - the last digit in the integer power of an integer is 8, 4, 2, 6, 8, ...
-
-
4 - the cyclisity is equal to 2
-
the last digit in the odd integer power of an integer is 4, i.e. 4, 4, 4, 4, ...
-
the last digit in the even integer power of an integer is 6. i.e. 4, 6, 6, 6, ...
-
-
9 - the cyclisity is equal to 2
-
the last digit in the odd integer power of an integer is 9, i.e. 9, 9, 9, 9, ...
-
the last digit in the even integer power of an integer is 1. i.e. 9, 1, 1, 1, ...
-
Greatest Common Divisior (GCD)
The greatest common divisor (gcd), or greatest common factor (gcf), or highest common factor (hcf) of a set of two or more non-zero integers is the largest positive integer that can divide the set of integers without a remainder. In order to find the common factor, the prime factorization should be used for determining the factors of all numbers. The greatest common factor of the set of numbers can be obtained by multiplying the greatest common factors of all prime factors of the set of numbers, i.e. multiply the lowest power of common prime factors. imply
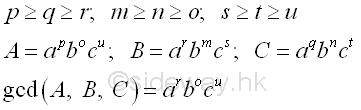
Therefore every common factor of the set of numbers is a divisor of the greatest common divisor, gcd, of the set of numebrs.
Euclidean algorithm
Euclidean algorithm or Euclid's algorithm is an effective technique to determine the greatest common factor GCD of two numbers through iteration. The Euclidean algorithm makes use of the greatest common factor proporty of two numbers by assuming the two numbers as the multiples of the two numbers and then reducing the multiple factors through iteration. Imply

The iterative steps of Euclidean algorithm or Euclid's algorithm can be expressed as a recursive equation, imply
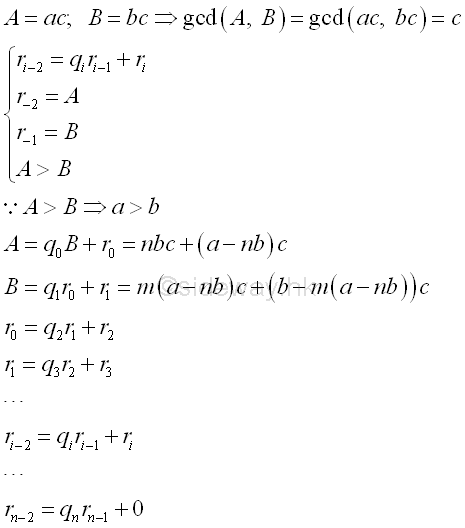
Bezout's Identity
By reversing the Euclidean algorithm or Euclid's algorithm, the greatest common factor GCD of two numbers can be expressed the sume of two numbers which are obtained by multiplying a positive and a negative integers to the original numbers respectively in the form of ax+by=d where x and y are integers of Bezout coefficients of integers a and b and integer d is the common divisor of integers a and b. Imply
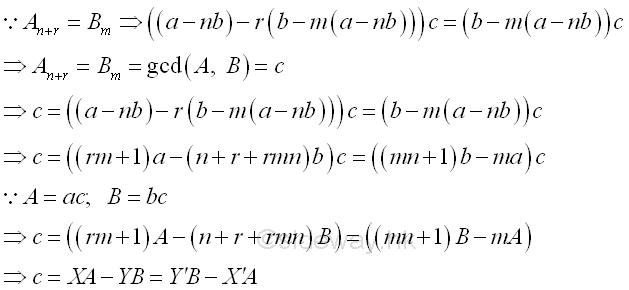
Least Common Multiple (LCM)
The least common multiple (lcm), or lowest common multiple (lcm), or smallest common multiple (scm) of a set of two or more non-zero integers is the least positive integer that can be divided by the set of integers without a remainder. In order to find the common multiple, the prime factorization should be used for determining the factors of all numbers. The least common multiple of the set of numbers can be obtained by multiplying the least common multiples of all prime factors of the set of numbers, i.e. multiply the highest power of common prime factors. imply
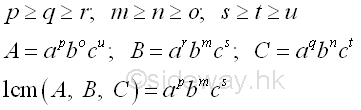
If one of the number is equal to 0, then the least common multiple, lcm, is defined as zero.
Besides, the product of two numbers can be expressed the product of least common multiple and greatest common divisior of the two numbers. Imply
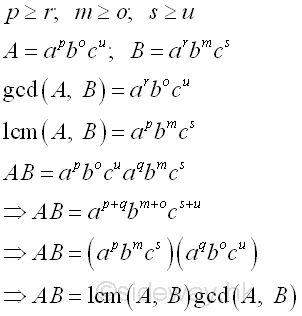
Modular Arithmetic
Modular arithmetic is also call clock arithmetic because modular arithmetic is a arithmetic for integers with number line wrap around like a clock, where number counting from 0 to a number m-1 for modulus m cyclically . e.g. number line of modulus 12 is 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 0, 1, 2,...
Let q be the quotient and r be the remainde when a number x is divided by modulus m. Imply
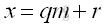
The remainder can be represented by
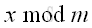
Let p be the quotient and r be the remainder when a number y is divided by modulus m. Imply

The remainder can be represented by
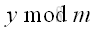
For m≥2, both x and y have the same remainder when divided by m, the relationship between x and y can be expressed as
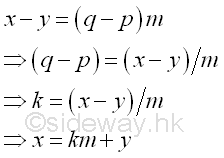
Since q, and p are integers, k is integer also. In other words, m divides (x-y)
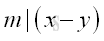
Therefore both x and y are equivalent modulo m, x and y are said to be congruent modulo m, or x is congruent to y modulo m. Imply
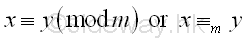
©sideway
ID: 120400009 Last Updated: 4/26/2012 Revision: 0
Latest Updated Links
- Pentium(last updated On 7/3/2025)
- Intel CPU(last updated On 7/2/2025)
- Intel CPU History(last updated On 7/1/2025)
- FreeGLUT Windows Function(last updated On 1/27/2025)
- FreeGLUT Initialization Function(last updated On 1/26/2025)
- FreeGLUT(last updated On 1/25/2025)
- GLUT(last updated On 1/24/2025)
- OpenGL(last updated On 1/23/2025)
- XPower UC140 4-Port 140W PD3.1 GaN Travel Charger(last updated On 1/22/2025)
- XPower DX6 6 In 1 (2x3) 60W PD3.0 Sync & Charge Cable(last updated On 1/21/2025)
- XPower MF240 1.2M Magnetic Absorption 4 in 1 (2x2) Zinc Alloy 240W PD Sync & Charge Cable(last updated On 1/20/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Computer
Hardware 257
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
