Content
Primality
Primality and Factorization
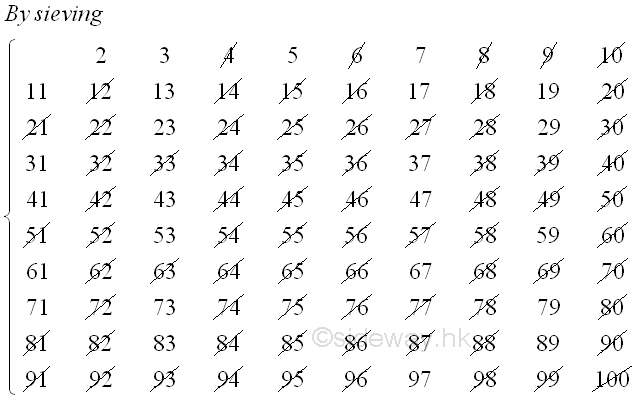
The Sieve of Eratosthenes (c 3 BC)[1]
Fermat's Little Theorem[1]
The Order of "a" Modulo "p" [1]
Primitive Roots Modulo a prime p[1]
Primality
Prime numbers are natural numbers, e.g. 2, 3, 5, 7,..., which can only be divided by 1 and itself. Although the way to recognize the primality of a natural numbe is very simple, there is difficulty of distinguishing prime numbers from composite numbers when natural numbers become very large.
Primality and Factorization
In general, the problem of primality and factorization of a large natural number is the involving of finitely many steps. The simple algorithm for the problem of primality and factorization is the method of trial division. For a given natural number N, a division test can be used to determine whether the natural number N is a prime or a composite number. The division test can be tried in succession of every number n=2,3,4,...,⌊√N⌋ to check whether n divides N or not. Composite number in the list can also be ignored from the division test. If none of the prime number in the list can divide N, then N is a prime. The problem with the trial division is the time consumption on determining whether a large number is a prime or composite.
The Sieve of Eratosthenes (c 3 BC)[1]
Instead of trial division, Eratosthenes making use of multiplication, an easier operation than division to sieve out composite number of the multiples of primes p for all p2≤N in an organized way. The sieving process starts from the smallest prime p=2, all multiples of the prime p, which are bigger than prime p, are crossed out. The process is repeated until p=⌊√N⌋. For example, all composite number small or equal to 100 can be sifted away after sieving with multiples of number 2, 3, 5, and 7. Numbers 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, and 97 are primes. Imply
Fermat's Little Theorem[1]
Although the Sieve of Eratosthenes has much improved the method of trial division, the Sieve of Eratosthenes is still a time consuming process. Methods are developed to reduce the time required for test primality. One type of classical methods is making use of theorems on congruences. One important theorem on primality testing is the Fermat's Little Theorem. The Fermat's Little Theorem state that if p is a prime and a is any positive integer then ap≡ a(mod p). And if integer a is not divisible by a, then ap-1≡ 1(mod p). The proof of Fermat's Little Theorem is first published by Euler in 1736. Let a be equal to 1, Euler's first proof proves the stated lemma is true at a=2 by the binomial expansion of 2 in the form of 1+1. Imply

Euler's second proof proves the Fermat's Little Theorem is true at a=2 by the binomial expansion of 2 in the form of 1+1 directly and give an alternate approach to prove the stated lemma is true. Imply
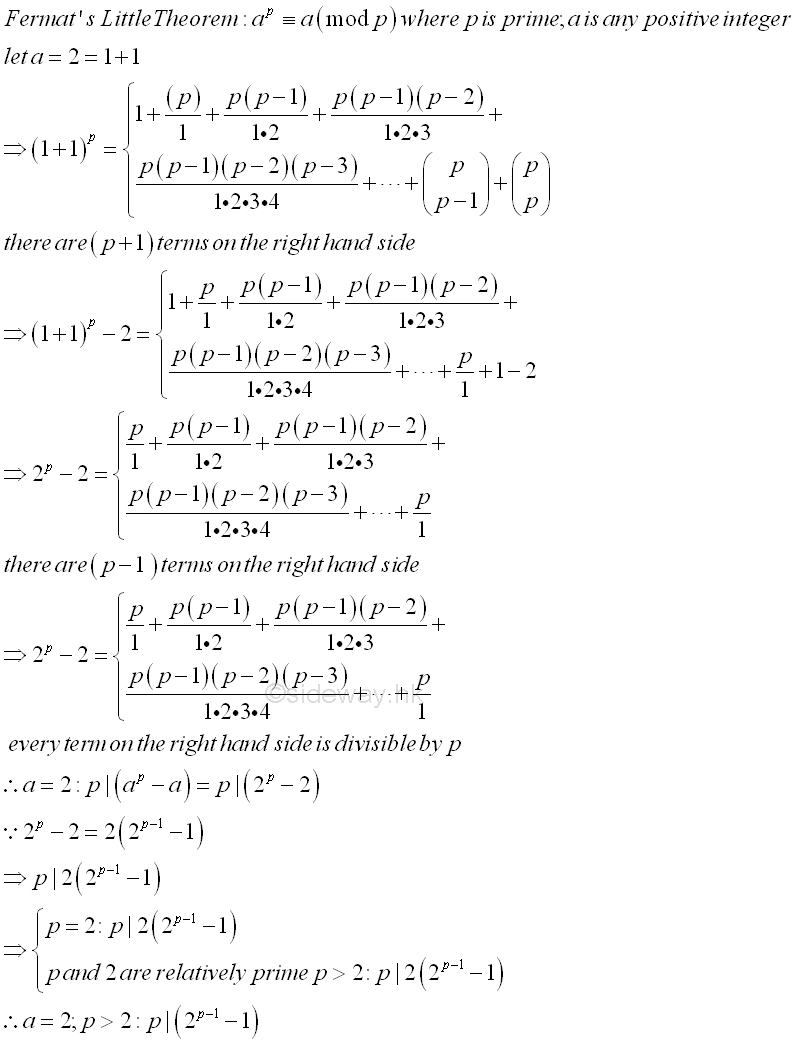
Euler's third proof proves both the Fermat's Little Theorem and the stated Lemma is also true at a=3 by the binomial expansion of 3 in the form of 1+2 directly in a similar way. Imply
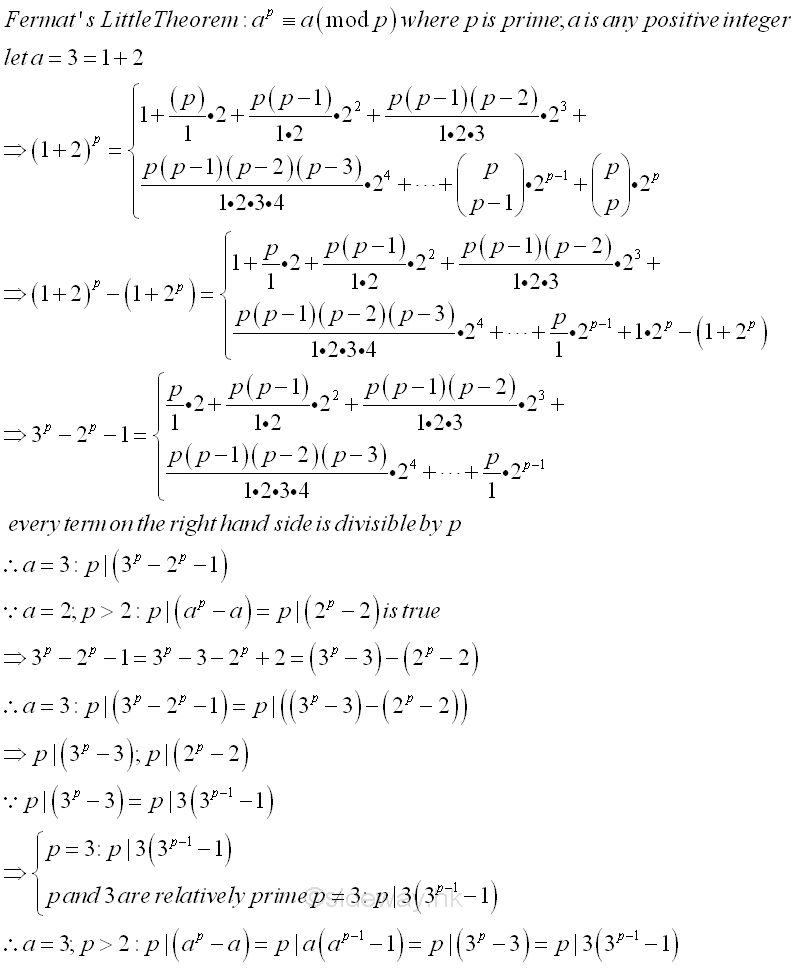
Similar to the proof on case a=3, Euler proves both the Fermat's Little Theorem and the stated Lemma is also true at a general case using the binomial expansion of a in the form of 1+a directly by general induction step. Imply

The proof is making use of the property of the binomial coefficient which based on the fact that if p is a prime then the binomial coefficient of term k such that 0<1≤k≤p-1<p should always be divided by p since the binomial coefficient is an integer and p is not divisible by any factors of the denominator of the binomial coefficient. prime p is the common factor of the binomial coefficient. The Fermat's Little Theorem can be used to identify one of the crucial property of a prime number. However, the Fermat's Little Theorem is also valid for some composite number, called Fermat pseudoprime. This is because there are two more variables in each binomial term besides the binomial coefficient. Therefore the Fermat's Little Theorem can only be true for sieving out composite numbers, more or repeated tests is needed to confirm the tested number is a prime. Besides for a composite number of a power of p, if p∤a and pe is the highest power of p divides ap-1-1 then pe+n is the highest power of p divides ape(p-1)-1.
Euler in 1736 expand the proof to a general form. If p is a prime and a and b are any integer then all number in the form of (a+b)p-ap-bp is divisible by p. The proof is same as before and the number 1 in 1+a is replaced by b, i.e. a+b. Imply

The Order of "a" Modulo "p" [1]
In 1758, Euler further extend the proof to the division of powers. If p is prime, a is any integer, and gcd(a,p)=1, there exists an infinite geometric progression {1, a, a2, a3,a4,... ,ar, ...} where r is an integer, then there are infinitely many terms which remain a residue 1 when divided by p and the exponents of those terms that divided by p with remainder 1 will form an arithmetic progression.
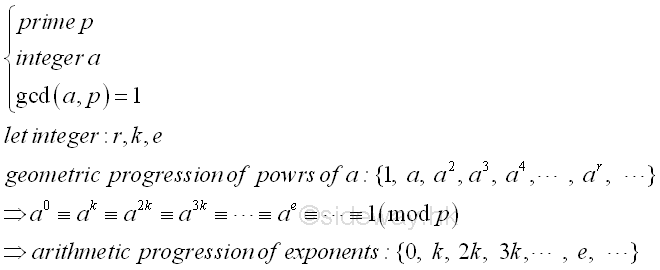
If aλ is the smallest power of a that have remainder 1 after divided by prime p, then all remainders of the terms in the geometric progression {1, a, a2, a3,a4,... ,aλ-1} up to term aλ is distinct. Since whenever there are two terms in the geometric progression having the same remainder, there must have one more term while i≠j with remainder equal to 1 below ,aλ such that the proposed λ is not the smallest. Imply
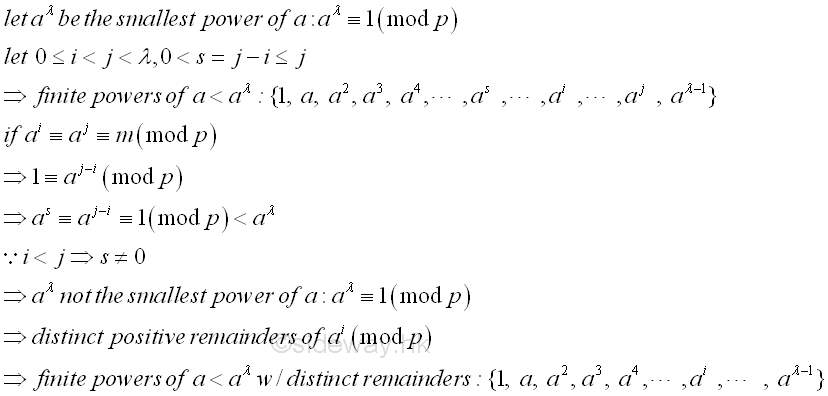
In general, there have p-1 positive distinct residues less than p when an integer is divided by p. Therefore, let p is a prime number and a is prime to p, if all the positive numbers less than p are represented by the residues of the powers of a divided by p, then ap-1 will be the smallest power which have remainder 1 when divided by p. That is the orders of a are λ=p-1 (mod p). Since there are only maximum p-1 distinct positive remainders when an integer is divided by p and the remainders of the finite set of the power of a less than aλ are distinct and λ, the maximum number of terms in the finite site of the power of a less than aλ are less or equal to p-1 and . Consider the case λ=p-1. If ai≡a0≡1(mod p), then ai+1=a1(mod p). Since when i is 0<i<p-1, the remainder will appear twice and contradicts to the result of distinct positive remainders, therefore i should equal or greater than p-1 and ap-1 will be the smallest power of a with remainder 1 when divided by p, that is ap-1≡1(mod p) and ap≡a(mod p). The p-1 is also the constant of the arithmetic progression of the exponent, i.e. k=p-1. Imply

However for some a, the order f is less then p-1 such that not all positive numbers less than p are represented by the residues of the powers of a divided by p. In other words, there exists some possible remainders which are not the residue of powers of a when divided by p. From Fermat's Little Theorem, p is prime and p|(ap-1-1) (mod p) then ap-1 always have a remainder 1 when dividing p. And for the smallest power of the order λ which have remainder 1 when dividing p, the set of exponents is an arithmetic progression with a constant of λ. That is {0,λ,2λ,3λ,4λ,...}. Since p-1 must be in the set of the arithmetic progression with a constant λ.Therefore, if p is prime and aλ is the smallest power of a when divided by p with remainder 1, then will the exponent λ will be a divisor of the number p-1. Imply

As a result, for any integer a and a prime p, if a is not a multiple of the prime p, there exists the smallest exponent λ, such that aλ≡1 (mod p). And for any other exponent i, ai≡1 (mod p) is valid if and only if f divides i. and the particular case is f divides p-1. The exponent λ is called the order of "a" modulo "p". The residues of the power of a divided by p are still distinct and only some of the residues less than p when a is divided by p, are not the residues of the power of a divided by p.
| p=3 | p=5 | p=7 | p=11 | p=13 | p=17 | p=19 | p=23 | p=29 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a=2 | a=2 | a=3 | a=2 | a=3 | a=5 | a=2 | a=3 | a=5 | a=2 | a=3 | a=2 | a=3 | a=2 | a=3 | a=2 | a=3 | a=2 | a=3 |
| 20=1 | 20=1 | 30=1 | 20=1 | 30=1 | 50=1 | 20=1 | 30=1 | 50=1 | 20=1 | 30=1 | 20=1 | 30=1 | 20=1 | 30=1 | 20=1 | 30=1 | 20=1 | 30=1 |
| 21=2 | 21=2 | 31=3 | 21=2 | 31=3 | 51=5 | 21=2 | 31=3 | 51=5 | 21=2 | 31=3 | 21=2 | 31=3 | 21=2 | 31=3 | 21=2 | 31=3 | 21=2 | 31=3 |
| 22=1 | 22=4 | 32=4 | 22=4 | 32=2 | 52=4 | 22=4 | 32=9 | 52=3 | 22=4 | 32=9 | 22=4 | 32=9 | 22=4 | 32=9 | 22=4 | 32=9 | 22=4 | 32=9 |
| 23=3 | 33=2 | 23=1 | 33=6 | 53=6 | 23=8 | 33=5 | 53=4 | 23=8 | 33=1 | 23=8 | 33=10 | 23=8 | 33=8 | 23=8 | 33=4 | 23=8 | 33=27 | |
| 24=1 | 34=1 | 24=2 | 34=4 | 54=2 | 24=5 | 34=4 | 54=9 | 24=3 | 34=3 | 24=16 | 34=13 | 24=16 | 34=5 | 24=16 | 34=12 | 24=16 | 34=23 | |
| 25=4 | 35=5 | 55=3 | 25=10 | 35=1 | 55=1 | 25=6 | 35=9 | 25=15 | 35=12 | 25=13 | 35=15 | 25=9 | 35=13 | 25=3 | 35=11 | |||
| 26=1 | 36=1 | 56=1 | 26=9 | 36=3 | 56=5 | 26=12 | 36=1 | 26=13 | 36=2 | 26=7 | 36=7 | 26=18 | 36=16 | 26=6 | 36=4 | |||
| 27=7 | 37=9 | 57=3 | 27=11 | 37=3 | 27=9 | 37=6 | 27=14 | 37=2 | 27=13 | 37=2 | 27=12 | 37=12 | ||||||
| 28=3 | 38=5 | 58=4 | 28=9 | 38=9 | 28=1 | 38=1 | 28=9 | 38=6 | 28=3 | 38=6 | 28=24 | 38=7 | ||||||
| 29=6 | 39=4 | 59=9 | 29=5 | 39=1 | 29=2 | 39=3 | 29=18 | 39=18 | 29=6 | 39=18 | 29=19 | 39=21 | ||||||
| 210=1 | 310=1 | 510=1 | 210=10 | 310=3 | 210=4 | 310=9 | 210=17 | 310=16 | 210=12 | 310=8 | 210=9 | 310=5 | ||||||
| 211=7 | 311=9 | 211=8 | 311=10 | 211=15 | 311=10 | 211=1 | 311=1 | 211=18 | 311=15 | |||||||||
| 212=1 | 312=1 | 212=16 | 312=13 | 212=11 | 312=11 | 212=2 | 312=3 | 212=7 | 312=16 | |||||||||
| 213=15 | 313=12 | 213=3 | 313=14 | 213=4 | 313=9 | 213=14 | 313=19 | |||||||||||
| 214=13 | 314=2 | 214=6 | 314=4 | 214=8 | 314=4 | 214=28 | 314=28 | |||||||||||
| 215=9 | 315=6 | 215=12 | 315=12 | 215=16 | 315=12 | 215=27 | 315=26 | |||||||||||
| 216=1 | 316=1 | 216=5 | 316=17 | 216=9 | 316=13 | 216=25 | 316=20 | |||||||||||
| 217=10 | 317=13 | 217=18 | 317=16 | 217=21 | 317=2 | |||||||||||||
| 218=1 | 318=1 | 218=13 | 318=2 | 218=13 | 318=6 | |||||||||||||
| 219=3 | 319=6 | 219=26 | 319=18 | |||||||||||||||
| 220=6 | 320=18 | 220=23 | 320=25 | |||||||||||||||
| 221=12 | 321=8 | 221=17 | 321=17 | |||||||||||||||
| 222=1 | 322=1 | 222=5 | 322=22 | |||||||||||||||
| 223=10 | 323=8 | |||||||||||||||||
| 224=20 | 324=24 | |||||||||||||||||
| 225=11 | 325=14 | |||||||||||||||||
| 226=22 | 326=13 | |||||||||||||||||
| 227=15 | 327=10 | |||||||||||||||||
| 228=1 | 328=1 |
Let t be the order of "a" modulo "p", the set of the power of a divided by p with distinct residue is {1,a,a2,...,at-1} If t<p-1, then there exists a positive integer k of 1<k<p is not the residue of a power of a. A new set with the multiplication of k can be constructed {k,ka,ka2,...,kat-1}, which has distinct residues when divided by p and no one is the residue of the power of a(mod p). The new set has distinct residues because whenever there are two terms in the geometric progression having the same remainder, they will cause contradiction to the set of the power of a with the order of "a" modulo "p" equals to t. There is also no duplicate residues in the two sets of powers of a Imply

There are totally 2t distinct residues (mod p) in sets {1,a,a2,...,at-1} and {k,ka,ka2,...,kat-1}. Since the order of "a" modulo "p" is equal to t and t<p-1, imply 2t≤p-1. If 2t=p-1, then t|(p-1). If 2t<p-1 then try another integer f. Similar to k, a new set {f,fa,fa2,...,fat-1}, which has distinct residues when divided by p and no one is the residue of ai or kai (mod p). Then there are totally 3t distinct residues (mod p) in sets {1,a,a2,...,at-1}, {k,ka,ka2,...,kat-1}, and {f,fa,fa2,...,fat-1}. Similarly if 3t=p-1, then t|(p-1). If 3t<p-1 then try another integer again.
| p=7 | p=11 | p=13 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a=2 | a=2 | a=3 | a=5 | a=2 | a=3 | ||||||||||
| k=3 | k=5 | k=6 | k=2 | k=6 | k=2 | k=6 | k=2 | k=4 | k=7 | ||||||
| 20=1 | 3*20=3 | 5*20=5 | 6*20=6 | 20=1 | 30=1 | 2*30=2 | 2*30=2 | 50=1 | 2*50=2 | 6*50=6 | 20=1 | 30=1 | 2*30=2 | 4*30=4 | 4*30=7 |
| 21=2 | 3*21=6 | 5*21=3 | 6*21=5 | 21=2 | 31=3 | 2*31=6 | 2*31=6 | 51=5 | 2*51=10 | 6*51=8 | 21=2 | 31=3 | 2*31=6 | 4*31=12 | 4*31=8 |
| 22=4 | 3*22=5 | 5*22=6 | 6*22=3 | 22=4 | 32=9 | 2*32=7 | 2*32=7 | 52=3 | 2*52=6 | 6*52=7 | 22=4 | 32=9 | 2*32=5 | 4*32=10 | 4*32=11 |
| 23=1 | 3*23=3 | 5*23=5 | 6*23=6 | 23=8 | 33=5 | 2*33=10 | 2*33=10 | 53=4 | 2*53=8 | 6*53=2 | 23=8 | 33=1 | 2*33=2 | 4*33=4 | 4*33=7 |
| 24=2 | 3*24=6 | 5*24=3 | 6*24=5 | 24=5 | 34=4 | 2*34=8 | 2*34=8 | 54=9 | 2*54=7 | 6*54=10 | 24=3 | 34=3 | 2*34=6 | 4*34=12 | 4*34=8 |
| 25=4 | 3*25=5 | 5*25=6 | 6*25=3 | 25=10 | 35=1 | 2*35=2 | 2*35=2 | 55=1 | 2*55=2 | 6*55=6 | 25=6 | 35=9 | 2*35=5 | 4*35=10 | 4*35=11 |
| 26=1 | 3*26=3 | 5*26=5 | 6*26=6 | 26=9 | 36=3 | 2*36=6 | 2*36=6 | 56=5 | 2*56=10 | 6*56=8 | 26=12 | 36=1 | 2*36=2 | 4*36=4 | 4*36=7 |
| 27=7 | 37=9 | 2*37=7 | 2*37=7 | 57=3 | 2*57=6 | 6*57=7 | 27=11 | 37=3 | 2*37=6 | 4*37=12 | 4*37=8 | ||||
| 28=3 | 38=5 | 2*38=10 | 2*38=10 | 58=4 | 2*58=8 | 6*58=2 | 28=9 | 38=9 | 2*38=5 | 4*38=10 | 4*38=11 | ||||
| 29=6 | 39=4 | 2*39=8 | 2*39=8 | 59=9 | 2*59=7 | 6*59=3 | 29=5 | 39=1 | 2*39=2 | 4*39=4 | 4*39=7 | ||||
| 210=1 | 310=1 | 2*310=2 | 2*310=2 | 510=1 | 2*510=7 | 6*510=10 | 210=10 | 310=3 | 2*310=6 | 4*310=12 | 4*310=8 | ||||
| 211=7 | 311=9 | 2*311=5 | 4*311=10 | 4*311=11 | |||||||||||
| 212=1 | 312=1 | 2*312=2 | 4*312=4 | 4*312=7 |
Since p is a prime, and t≤p-1, eventulaly t divides p-1. Thus for some integer m, p-1=tm. Imply ap-1=atm, and ap-1≡atm(mod p), therefore ap-1≡atm≡(at)m≡1(mod p) since at≡1(mod p). If t≠p-1, then there always exists some m such that p-1=tm.
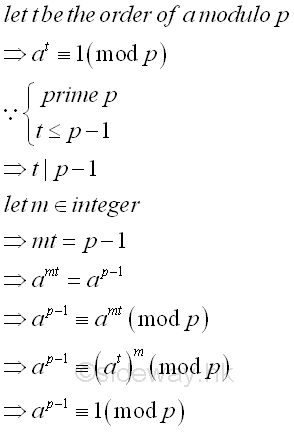
Since t is the least power of a that divided by p with remainder 1. therefore t always divides (p-1) and ap-1-1≡at-1≡0(mod p), there is a m such that mt=p-1. In other words, at≡a2t≡a3t≡...≡amt-2t≡amt-t≡amt≡1 or in term of p-1, ap-1-mt+t≡ap-1-mt+2t≡ap-1-mt+3t≡...≡ap-1-2t≡ap-1-t≡ap-1≡1. Since the difference between two terms is at, the difference of the multiplication of the sum of all terms by at and the sum of all terms is equal to zero, therefore at(ap-1-mt+t+ap-1-mt+2t+ap-1+mt+3t+...+ap-1-2t+ap-1-t+ap-1)-(ap-1-mt+t+ap-1-mt+2t+ap-1-mt+3t+...+ap-1-2t+ap-1-t+ap-1)≡0. Therefore (at-1)(ap-1-mt+t+ap-1-mt+2t+ap-1-mt+3t+...+ap-1-2t+ap-1-t+ap-1)≡ap-1-1≡0
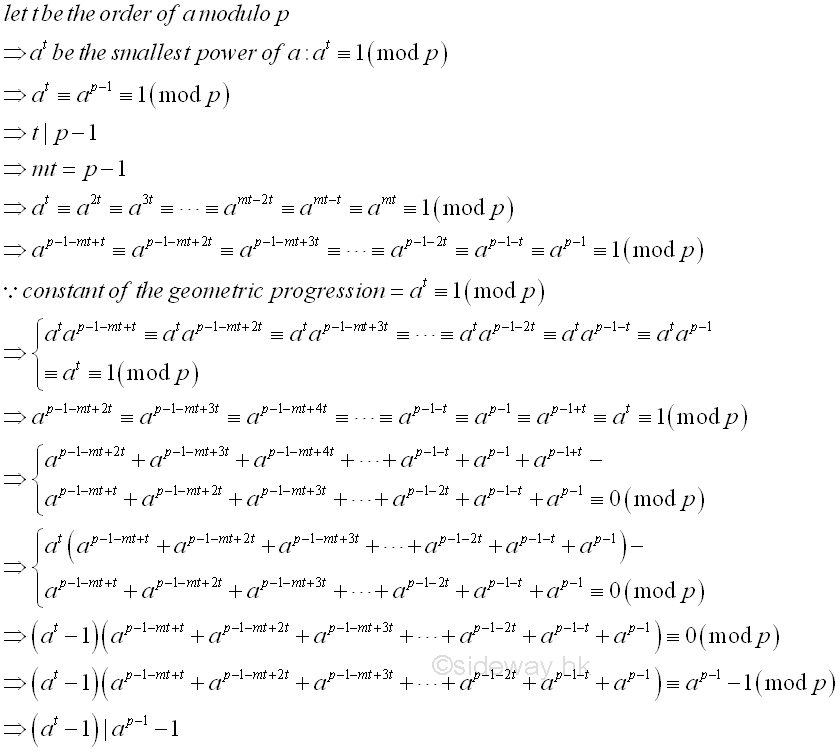
As a result, (at-1)|ap-1-1 also besides t|ap-1-1.
Primitive Roots Modulo a prime p[1]
Similar to changing the value of integer k for the order of a modulo p equals to
t and less then p-1, the integer a can also be altered such that the value of
the order of a modulo p is changed accordingly. Let p>2 and t≥1. If p-1 divides t, then jt≡1 (mod p) for j=1,2,3,...,p-2,p-1. The sum of
these terms is equal to S≡p-1≡-1 (mod p). Let g be a primitive root
modulo p. If p-1 does not divide t, then gt≢1(mod p). Since the set of residue class of g
modulo p of order p-1 is {1, 2,...,(p-2),(p-1)}, the set of residue class
with the multiplication of g to the residue is the same, {g,
g2,...,g(p-2),g(p-1)}. Therefore, for S≡∑ p-1
j=1 jt (mod p), imply ∑ p-1
j=1 (gj)t≡gt∑ p-1
j=1 jt≡gtS (mod
p). Since gt≢1(mod p), p does not divide gt-1, imply S≡0 (mod p). Imply

For every prime p, there always exists at least one integer g, not a multiple of the prime p, such that the order of g modulo p is equal to p-1. Therefore the distinct power set {g0,g1, g2,...,gp-2} is equal to the distinct residue set {1, 2,...,(p-2),(p-1)}. Every integer g with 1≤g≤p, such that g mod p has order p-1 is called a primitive root modulo p. One of the effective method is suggested by Gauss.
©sideway
ID: 130400010 Last Updated: 4/19/2013 Revision: 0 Ref:
References
- R. Paulo, 1996, The New Book of Prime Number Records
- Wolstenholme, R.J., 1862, On Certain Properties of Prime Numbers
- Mann, H.B., Shanks D., 1972, A Necessary and Sufficient Condition for Primality, and Its Source
- J.M Pollard, Kangaroos, 1975, A Monte Carlo Method for Factorization
Latest Updated Links
- Pentium(last updated On 7/3/2025)
- Intel CPU(last updated On 7/2/2025)
- Intel CPU History(last updated On 7/1/2025)
- FreeGLUT Windows Function(last updated On 1/27/2025)
- FreeGLUT Initialization Function(last updated On 1/26/2025)
- FreeGLUT(last updated On 1/25/2025)
- GLUT(last updated On 1/24/2025)
- OpenGL(last updated On 1/23/2025)
- XPower UC140 4-Port 140W PD3.1 GaN Travel Charger(last updated On 1/22/2025)
- XPower DX6 6 In 1 (2x3) 60W PD3.0 Sync & Charge Cable(last updated On 1/21/2025)
- XPower MF240 1.2M Magnetic Absorption 4 in 1 (2x2) Zinc Alloy 240W PD Sync & Charge Cable(last updated On 1/20/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Computer
Hardware 257
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
