Content

Primality

Prime numbers are natural numbers, e.g. 2, 3, 5, 7,..., which can only be divided by 1 and itself. Although the way to recognize the primality of a natural numbe is very simple, there is difficulty of distinguishing prime numbers from composite numbers when natural numbers become very large.

The Theorem of Wilson  (1770)[1]

The Theorem of Wilson is a corollary of Fermat's Little Theorem by Wilson in 1770, stated that If p is a prime, then (p-1)!≡-1 (mod p) without a proof. Lagrange proves the theorem of Wilson in 1773. Let the distinct residue set {1, 2,...,(p-2),(p-1)} of a number when divided by a prime p. By polynomial expansion, let
 f(x)=(x-1)(x-2)..(x-p+2)(x-p+1)=xp-1-A1xp-2+...-Ap-2x1+Ap-1x0.
By muliply both sides by x and substitute x by x-1. Or let
 h(x)=(x-1)(f(x-1))=(x-1)(x-2)(x-3)...(x-p+1)(x-p)=(x-1)p+A1(x-1)p-1+...+Ap-2(x-1)2+Ap-1(x-1)1.
Let q(x)=(x-p)(f(x)). Then
 q(x)=(x-p)(xp-1-A1xp-2+...-Ap-2x1+Ap-1x0)=h(x)=(x-1)p-A1(x-1)p-1+...-Ap-2(x-1)2+Ap-1(x-1)1.
Further expanding terms on both sides. By collecting like terms and Equating the coefficients of terms on both sides according. Imply 
A1=(p
2), 2A2=(p
3)+A1(p-1
2), 3A3=(p
4)+A1(p-1
3)+A2(p-2
2), ...,
kAk=(p
k+1)+A1(p-1
k)+A2(p-2
k-1)+...+Ak-2(p-k
3)+Ak-1(p-k+1
2), ... ,
(p-2)Ap-2=p+(p-1)A1+(p-2)A2+...+3Ap-3, (p-1)Ap-1=1+A1+A2+A3+...+Ap-3+Ap-2.  .  Since p|A1, then p|A2, then p|A3, ...,  then p|Ap-2, and therefore (p-1)Ap-1≡1 (mod p). Imply Ap-1≡-1 (mod p). From f(x),  Ap-1 is equal to (p-1)!, imply  (p-1)!≡-1 (mod p). Imply 

The theorem is also true for p=2. Since a composite number can be expressed as the multiplication of two numbers, so if p is a composite, it must be the product of two numbers smaller than p or (p-1)! must be the multiple of p. The theorem gives another important characterization of prime numbers and leds to the study of numbers of n!=1 and n!=1. However, this is not an effective method to test the primaity of a number because the calculation of p! involves log N steps.

The Property of Giuga (1950)[1]

From Fermat's Little theorem, jp-1≡1 (mod p) for j=1,2,3,...,p-2,p-1. The sum of these terms is equal to (p-1)≡-1 (mod p). Imply

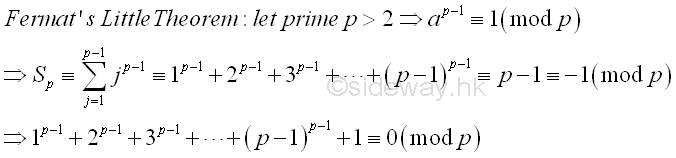
Giuga interested in whether the converse is true or not. That is whether n is a prime if n>1 and n divides 1n-1+2n-1+3n-1+...+(n-1)n-1+1. Or whether there are composite numbers such that n=pq where p is prime and p divides 1n-1+2n-1+3n-1+...+(n-1)n-1+1. That is  Gp≡∑ n-1
j=1jn-1+1≡0 (mod p)

The counter example, composite number,  to the Giuga condition is called a Giuga number. If n is a composite, let prime p divides n, then let n=pq. Consider the counter example, the sum of the power t=n-1 of the set of residue class when divided by prime p. That is S1≡∑ p-1
j=1jt≡∑ p-1
j=1jn-1≡{ -1 (mod p) if (p-1)|(n-1)
0 (mod p) if (p-1)∤(n-1),
therefore ∑ p-1
j=1q(j)n-1≡q∑ p-1
j=1jn-1≡qS1≡{ -q (mod p) if (p-1)|(n-1)
0 (mod p) if (p-1)∤(n-1).
Since n=pq, ∑ kp
j=kpjn-1≡0 (mod p), therefore
S2≡∑ n-1
j=1 jn-1≡∑ qp-1
j=(q-1)p+1 jn-1+∑ (q-1)p
j=(q-1)p jn-1+...+∑ 2p-1
j=p+1 jn-1+∑ p
j=p jn-1+∑ p-1
j=1 jn-1≡q∑ p-1
j=1 jn-1≡qS1≡{ -q (mod p) if (p-1)|(n-1)
0 (mod p) if (p-1)∤(n-1). 
Thus for each prime divisor p, substitute S2 into Gp, imply Gp≡{ -q+1 (mod p) if (p-1)|(n-1)
0+1 (mod p) if (p-1)∤(n-1)≡0 (mod p).

Thus if Gp≡0, then (p-1)|(n-1) where (n-1) is equal to pq-1=q(p-1)+(q-1), so (p-1) divides (q-1). From Gp, (-q+1)≡0 (mod p), imply q≡1 (mod p),then p divides (q-1) also. That is (p-1)|(q-1) and p|(q-1). Besides, since p|(q-1), imply p∤q, therefore n must be squarefree. Therefore with n is squarefree, (p-1)|(q-1) and p|(q-1), each of the distinct prime divisors p of n divides Gp , this is also true for n divides Gn. With (p-1)|(q=1) and p|(q-1), imply p2(q-1)  divides pq-p or n-p. Since n≡pq≡p≡0 (mod p) and (p-1) divides (q-1), imply p|n and n≡pq-1≡q(p-1)+(q-1)≡p≡1 (mod p-1).

The Wolstenholme's Theorem (1862)[1]

Another property of prime is from wolstenholme, proved in 1862 that if p is a prime greater or equal to 5 then p2 divides the numerator of 1+1⁄2+1⁄3+...+1⁄p-1 and p divides the numerator of 1+1⁄22+1⁄32+...+1⁄(p-1)2. And prime n greater than 3, n3 divides the combination of 2n-1 takes n-1 minus 1

Let H(p-1)= 1⁄1+1⁄2+1⁄3+...+1⁄p-2+1⁄p-1. By terms rearrangement, H(p-1)=(1⁄1+1⁄(p-1))+(1⁄2+1⁄(p-2))+...+(1⁄((p-1)/2)+1⁄(p-((p-1)/2))) = (((p-1)+1)⁄((1)(p-1)))+(((p-2)+2)⁄((2)(p-2)))+...+(((p-(p-1)/2)+((p-1)/2))⁄((p-1)/2)(p-(p-1)/2)) = (p⁄((1)(p-1)))+(p⁄((2)(p-2)))+...+(p⁄((p-1)/2)(p-(p-1)/2)) = p((1⁄((1)(p-1)))+(1⁄((2)(p-2)))+...+(1⁄((p-1)/2)(p-(p-1)/2))) . The denominators of H(p-1) can be reduced to the least common denominator of the denominators. The numerator of fractions of H(p-1) can then be replaced by an integer A.  Imply H(p-1)=pA⁄(p-1)!. Where A is equal to ((p-1)!⁄((1)(p-1)))+((p-1)!⁄((2)(p-2)))+...+((p-1)!⁄((p-1)/2)(p-(p-1)/2)) Since no factor in (p-1)! can divide p, the p must divide the numerator of H(p-1).

Let Ak=(p-1)!/(k(p-k)), then (k(p-k))Ak=(p-1)!. By Wilson's Theorem, (k(p-k))Ak≡(p-1)!≡-1 (mod p). Imply (pkAk-k2Ak)≡-k2Ak≡-1 (mod p). Imply k2Ak≡1 (mod p). Therefore Ak≡(p-1)!/(k(p-k))≡(k2)-1 (mod p). As k≢0 (mod p), Ak≡(p-1)!/(k(p-k))≡(k2)-1≡(k-1)2 (mod p). Imply A≡(12)-1+(22)-1+...+(k2)-1+...+(((p-1)/2)2)-1≡(1-1)2+(2-1)2+...+(k-1)2+...+(((p-1)/2)-1)2 (mod p) Since k2≡(-k)2 and (-k-1)≡-(k)-1 (mod p). Therefore A+A which is equal to (1-1)2+(2-1)2+...+(k-1)2+...+(((p-1)/2)-1)2+(1-1)2+(2-1)2+...+(k-1)2+...+(((p-1)/2)-1)2 (mod p) can be expressed as
 (1-1)2+(2-1)2+...+(k-1)2+...+(((p-1)/2)-1)2+(-(1-1))2+(-(2-1))2+...+(-(k-1))2+...+(-(((p-1)/2)-1))2 (mod p) ≡ (1-1)2+(2-1)2+...+(k-1)2+...+(((p-1)/2)-1)2+((-1)-1)2+((-2)-1)2+...+((-k)-1)2+...+((-((p-1)/2))-1)2 (mod p). Since -1≡p-1 (mod p), therefore
 A+A≡(1-1)2+(2-1)2+...+(k-1)2+...+(((p-1)/2)-1)2+((p-1)-1)2+((p-2)-1)2+...+((p-k)-1)2+...+((p-((p-1)/2))-1)2 (mod p). After rearrangement
 A+A≡(1-1)2+(2-1)2+...+(k-1)2+...+(((p-1)/2)-1)2+(((p+1)/2)-1)2+...+((p-k)-1)2+...+((p-2)-1)2+((p-1)-1)2 (mod p). Imply A+A≡(1-1)2+(2-1)2+...+(k-1)2+...+((p-2)-1)2+((p-1)-1)2 (mod p). Since both the number and its modular inverse sets of modulo prime p are equal to the same subset of the set {1,2,3,...,(p-1)}, imply 12+22+...+(p-1)2≡(1-1)2+(2-1)2+...+((p-1)-1)2 (mod p). Imply A+A≡(1)2+(2)2+...+(k)2+...+((p-2))2+((p-1))2 (mod p). As the sum of series of squares 12+22+...+(p-1)2 is equal to ((p-1)((p-1)+1)(2(p-1)+1))/6=((p-1)(p)(2p-1))/6, imply 6 divides ((p-1)(p)(2p-1)). As 6 does not divide p, then 6 divides ((p-1)(2p-1)). Therefore 12+22+...+(p-1)2≡((p-1)((p-1)+1)(2(p-1)+1))/6≡0 (mod p). Imply A+A≡(1)2+(2)2+...+(k)2+...+((p-2))2+((p-1))2≡0 (mod p).

 

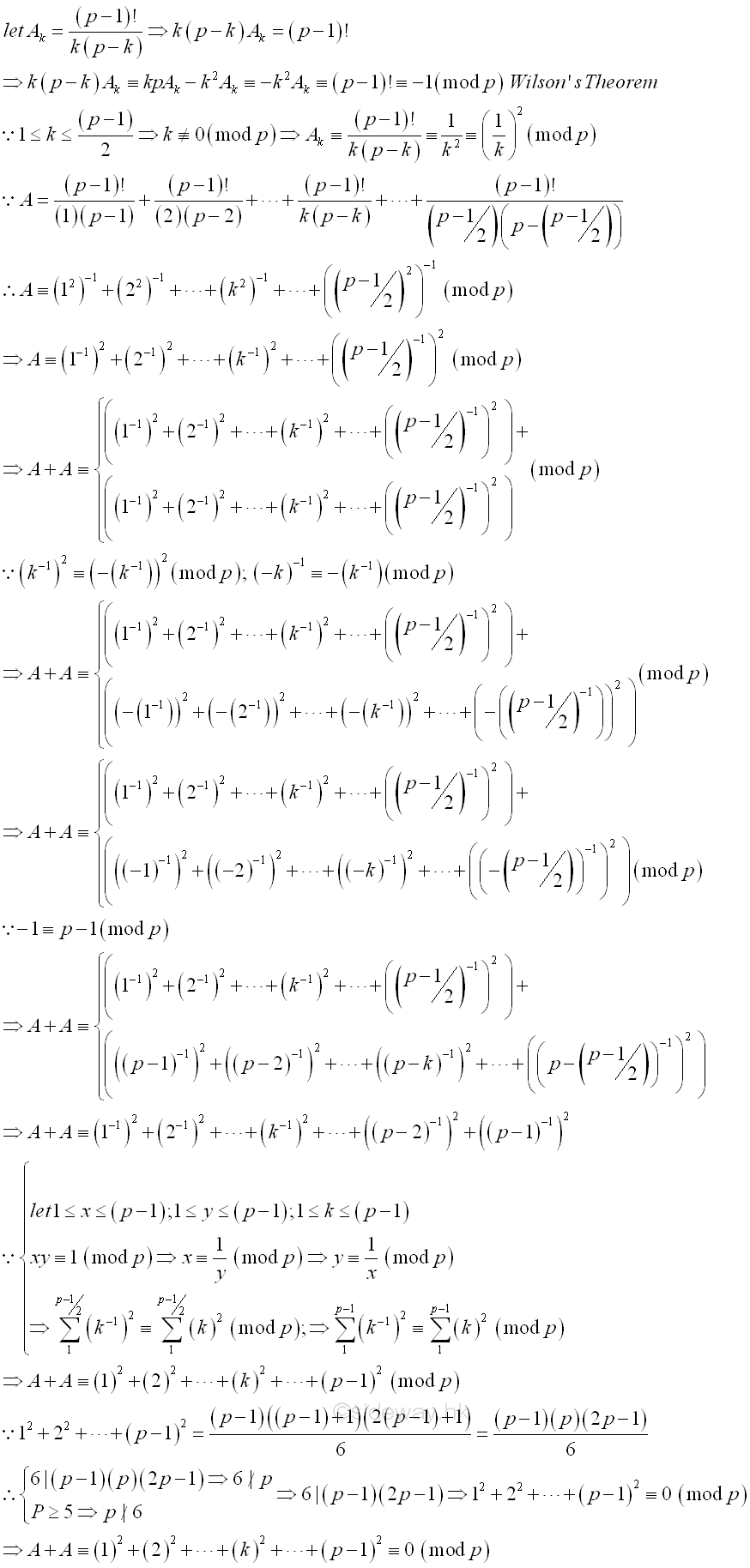
Thus 2A≡0 (mod p). Since 2∤p, imply p|A, that is A≡0 (mod p). Therefore A can be expressed as pB where B is an integer and substitute into H, that is H(p-1)≡pA/(p-1)!≡p2B/(p-1)! (mod p). As none of the factors in the denominator of H(p-1) can divide p, p2 must divide the numerator of H(p-1)=1⁄1+1⁄2+1⁄3+...+1⁄p-2+1⁄p-1. Since p divides 2A ,  2A=1⁄12+1⁄22+1⁄32+...+1⁄(p-1)2 , 6 does not divide p and as p greater or equal to 5, p does not divide 6 also. Imply p divides the numerator of 1⁄12+1⁄22+1⁄32+...+1⁄(p-1)2  .

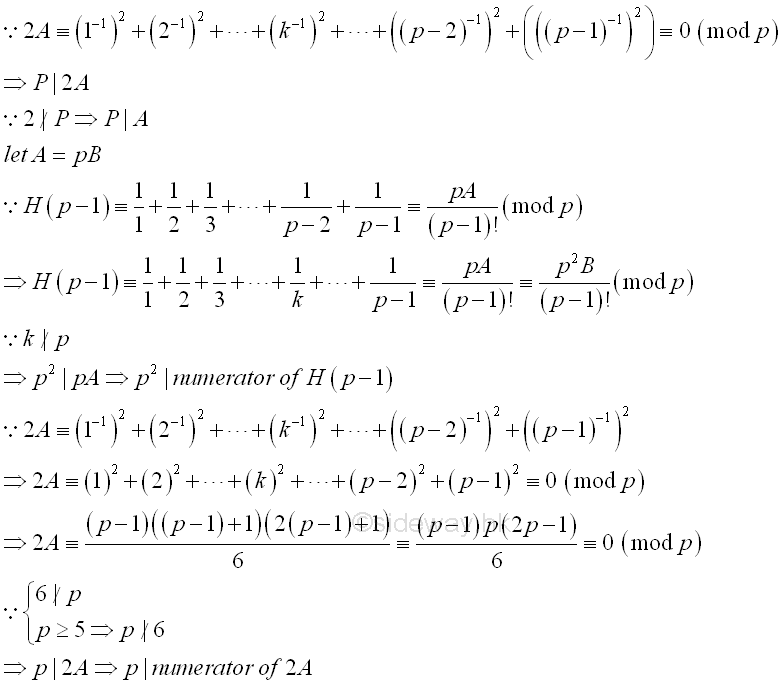
Based on these properties, wolstenholme generalizes to the property to the special case of n-1 combinations of 2n-1 is equivalent to 1 when divided by n3. The series 1+1⁄2+1⁄3+...+1⁄n-1 can be obtained from a combinatorial series.

If n is a prime greater than 2, then n is odd and the sign of coefficient of f(n-1) can be fixed. Therefore f(n-1) can be expressed as.

Part of the multiple of n2 of 2f(n-1) is represented by A. Further, part of the multiple of n of remaining 2f(n-1) can also be represented by B as following.

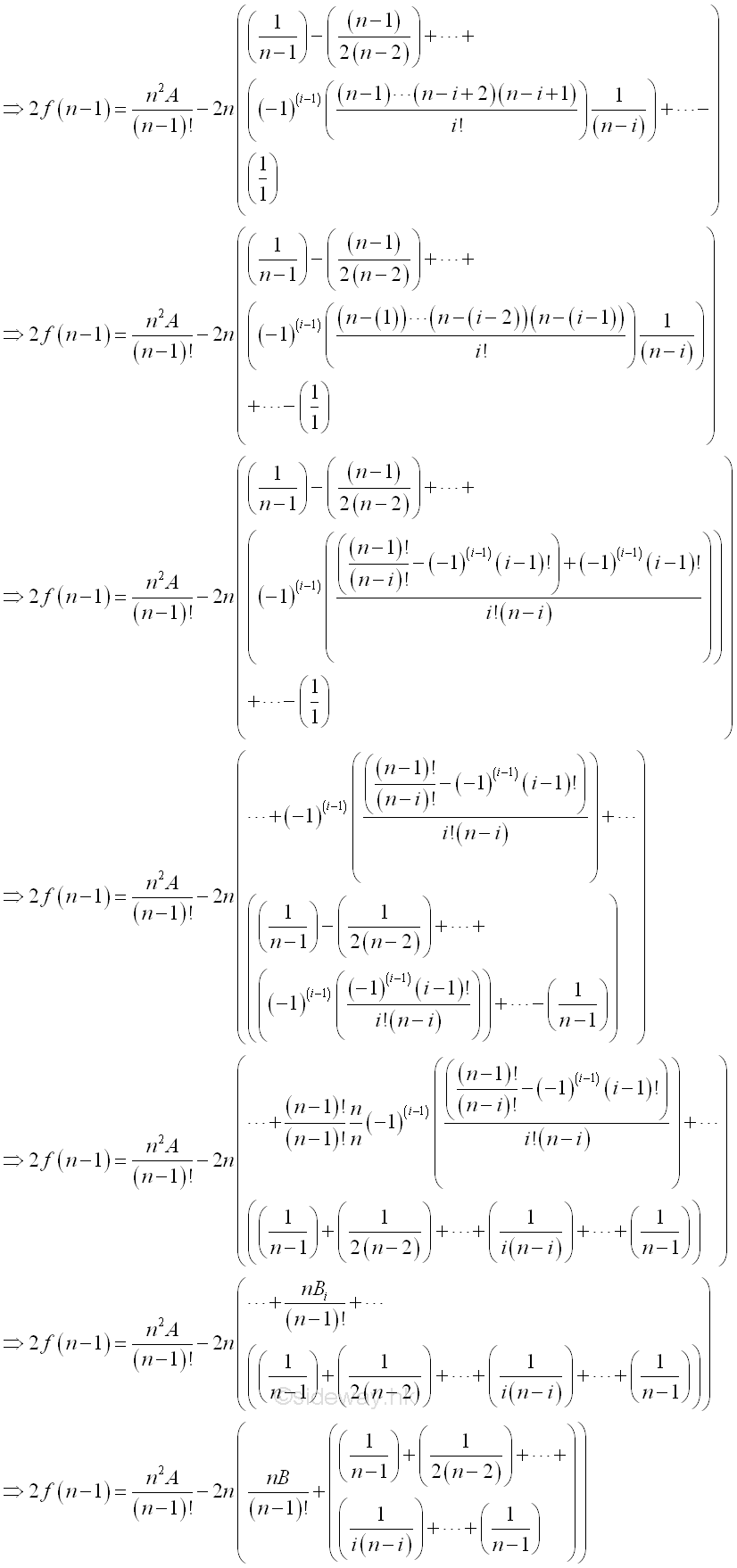
The part of the multiple of n can also be expressed in term of n2 also. Besides the remaining part can also be expressed in term of f(n-1). Imply.

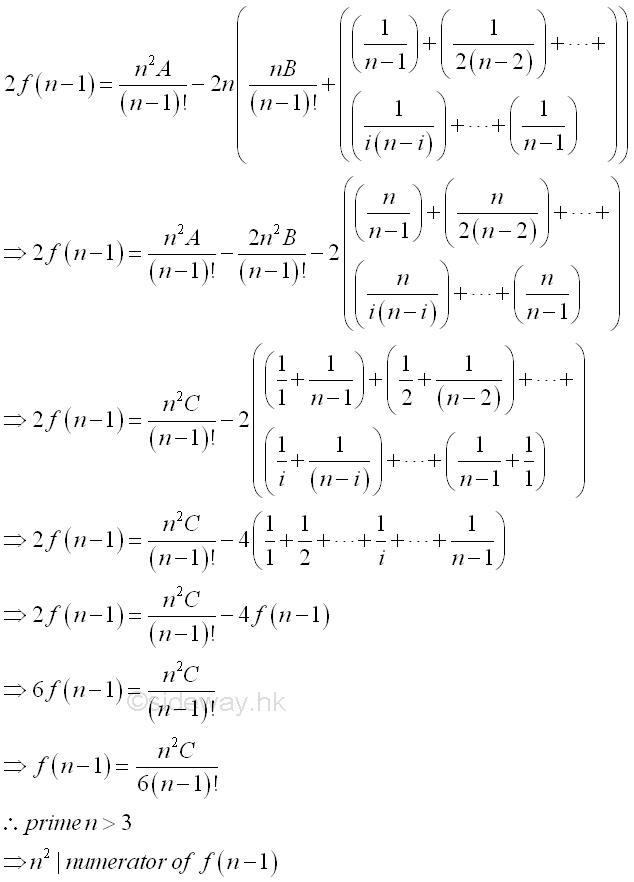
Therefore, if prime n greater than 3, n2 divides numerator of f(n-1). Similarly the series 1+1⁄22+1⁄32+...+1⁄(n-1)2 can also be obtained from f(n-1). Imply.

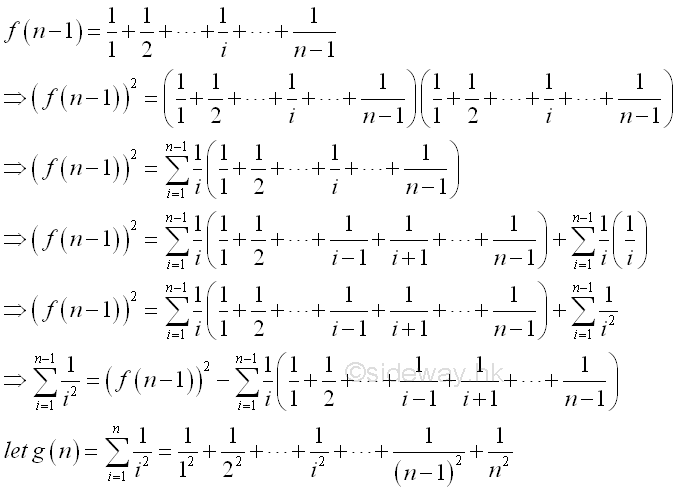
Similarly the series can be expressed in term of f(n-1) also. Imply.

Therefore, as limited by f(n-1), if prime n greater than 3, n2 divides numerator of g(n-1). Based on these properties, the combination of 2n-1 takes n-1 can also be expressed in terms of f(n-1). Imply.

Therefore, as limited by f(n-1), if prime n greater than 3, n3 divides the combination of 2n-1 takes n-1 minus 1.