Content
Factorization
Prime Factorization Trial Division
Fermat Factorization
Pollard
Rho Factorization
Factorization
Factorization is one of the methods to verify whether a number is prime.
Prime Factorization Trial Division
The direct search factorization is a bruce force factorization method for determining all possible prime factors of a composite number, N, through the repeated examination of divisibility by trial division from a set of non-trivial prime divisors.
Let x, y are non-trivial factors of integer N with N=xy. imply

It is not necessary to test all numbers from 1 to N-1.
If x, y are non-trivial factors of integer N with N=xy and x≤y, then x≤√N.
Since if x>√N, then y≥x>√N and imply xy>N, which contradicts to the assumption N=xy.
Therefore, the trial division can be performed by checking whether x divides N, x|N, for x=2 to the floor of √N. if x is found, imply x≡0 (mod N), and y, y=N/x is a factor also.
In verifying whether a number N is prime, x can be limited to a non-trivial prime factor.
Fermat Factorization
The Fermat factorization (1600s) from Pierre de Fermat is another way of factoring a composite number by considering the composite number as the difference of squares. This standard binomial can then be factorized into a product. Imply
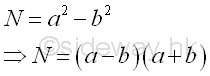
Since all even number can be divided by 2, let x, y are non-trivial odd factors of integer N with N=xy. imply

Equate two equations. Imply
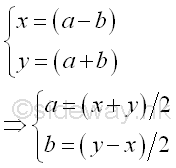
Both a and b are integers because x and y are odd integers, the sum and difference between any two odd number are even number which is divisible by 2. As x and y are non trivial factors, √N≥x>1 and y≥x, imply a≥1 and b≥0.
Instead of testing the non trivial factors x, and y, Fermat factorization examine the integers a and b. Imply

Therefore, the Fermat factorization can be performed by checking a from the floor of √N to N. whether the corresponding value of b is an integer and the corresponding terms of the product, (a-b) and (a+y) are the non trivial factors of N. Imply
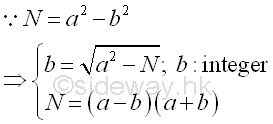
In verifying whether a number N is prime, the value of integer a should be choosen from the floor of √N to N.
Pollard Rho Factorization
The Pollard rho factorization or Pollard's Monte Carlo factorization method (1975) from J.M. Pollard is another technique of finding factors of a composite number by making use of probabilistic ideas from transforming a sequencial sequence to a congruential pseudo-random sequence to increase the probability of getting prime factors of the composite number.
©sideway
ID: 120400011 Last Updated: 4/17/2012 Revision: 0 Ref:
References
- R. Paulo, 1996, The New Book of Prime Number Records
- Wolstenholme, R.J., 1862, On Certain Properties of Prime Numbers
- Mann, H.B., Shanks D., 1972, A Necessary and Sufficient Condition for Primality, and Its Source
- J.M Pollard, Kangaroos, 1975, A Monte Carlo Method for Factorization
Latest Updated Links
- Ikea SANDSBERG table(last updated On 11/4/2025)
- Ikea TISKEN toilet roll holder(last updated On 11/3/2025)
- Philips CL400 Ceiling Light 36W(last updated On 11/2/2025)
- Philips CL400 Ceiling Light 24W(last updated On 11/1/2025)
- Philips CL400 Ceiling Light 13W(last updated On 10/30/2025)
- Ikea TISKEN basket(last updated On 10/29/2025)
- Ikea TISKEN towel rack(last updated On 10/28/2025)
- Ikea REXBEGONIA mattress protector(last updated On 10/27/2025)
- Ikea KEJSAROLVON mattress protector(last updated On 10/26/2025)
- Ikea KVARNVEN ergonomic pillow(last updated On 10/25/2025)
- Ikea BRUKSVARA pocket prung mattress(last updated On 10/24/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 27![]()
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
