Content
Sequence of First n Natural Numbers[1]
First n Natural Numbers Series[1]
Sequence of First n Natural Number Squares[1,2]
First n Natural Number Squares Series[1,2]
Sequence of First n Natural Number Cubes[1,2]
First n Natural Number Cubes Series[1,2]
Sequence of First n Natural Numbers[1]
The sequence of the first n natrual numbers are, 1, 2, 3, ...., n. The first n natural numbers sequence is an ordered arithmetic sequence with initial term equal to 1 and common difference equal to 1. Imply
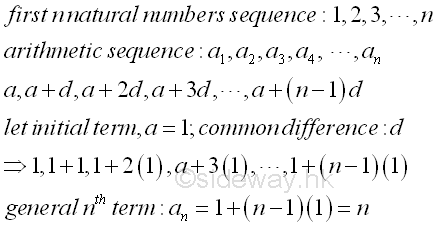
First n Natural Numbers Series[1]
Since the first n natural number is an arithmetic sequence, the series of the
first n natural numbers can also be determined as an arithmetic series. As an
arithmetic series is of the form S=a+(a+d)+(a+2d)+(a+3d)+.... And the general
format of an arithmetic series is Sn=a1+a2+a3+a4+
....+an-1+an =a+(a+d)+(a+2d)+(a+3d)+...+(a+(n-2)d)+(a+(n-1)d) =∑ n
i=1(ai) =∑ n-1
k=0 (a+kd) =1+2+3+4+
....+(n-1)+n . The sum of an arithmetic series can be determined by the
adding the reverse order of the arithmetic series to the original arithmetic
series, so that
the sum of two arithmetic series can be expressed as the sum of n equal
terms of first term plus last term. And the sum of arithmetic series is
therefore equal to n(2a+(n-1)d)/2=(n(n+1))/2. Imply
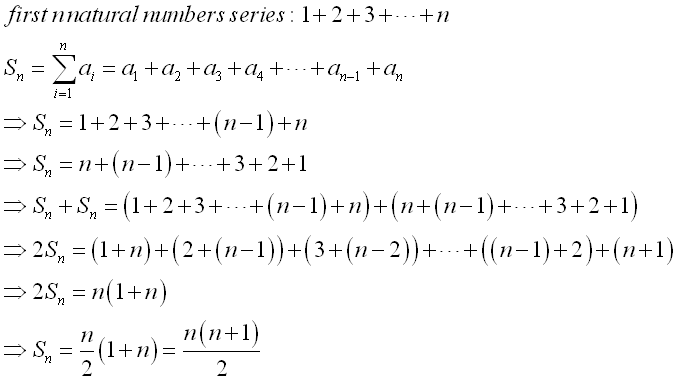
Sequence of First n Natural Number Squares[1,2]
The sequence of the first n natrual numbers squaes are, 1, 4, 9, ...., or 1,
22, 32, ...., n2. The
first n natural number squares sequence is an ordered sequence with initial
term equal to 1 and variable difference of two consecutive number squares equal to
k2-(k-1)2 =2k-1. That is 1, 1+(2(2)-1), 1+(2(2)-1)+(2(3)-1),
1+(2(2)-1)+(2(3)-1)+(2(4)-1),... or 1, 1+3, 1+3+5, 1+3+5+7,...,1+3+5+7+...+(2n-3)+(2n-1).
Therefore the general nth term is equal to an=n2=∑ n
i=1(2i-1).
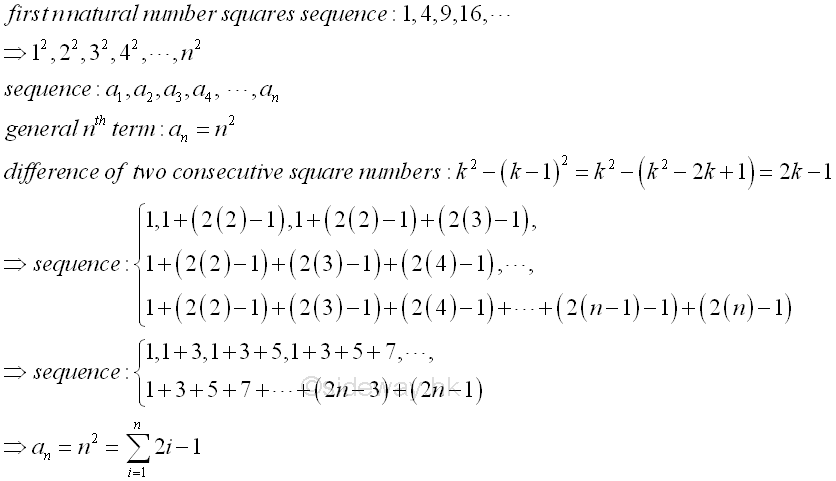
First n Natural Number Squares Series[1,2]
Since the common difference varies with the term, the sum of the sequence cannot be determined by the method of finding the sum of an arithmetic series directly. How the technique used to determine the sum of the first n natural number squares series is similarly. First, since the series of natural number squares has a variable difference equal to 2k-1, each term of the series can be expressed as a series, and the natural number since can be written as 1+(1+3)+(1+3+5)+(1+3+5+7+9)+...+(1+3+5+7+9+...+2n-3)+(1+3+5+7+9+...+2n-3+2n-1).

Second, apply the technique used in determining the sum of an arithmetic series, each series term of the series can be added to the reverse order of the series term itself, so that the sum of two natural number squares can be expressed in term of the sum of the first and last terms times the item number also. That is (1+1)+((1+3)+(3+1))+((1+5)+(3+3)+(5+1))+...+((1+(2n-1))+(3+(2n-3))+...+((2n-3)+3)+((2n-1)+1)) =(2)+(4+4)+(6+6+6)+...+(2n+2n+...+2n+2n).

Third, by comparing the new series of the sum of two series and the series of the original natural number squares series, there is similarity between the two series. For the original series, the total number of the same series item in the whole series number is in reversed order of the term number, i.e. n items of 1, n-1 items of 3, n-2 items of 5, ..., 1 item of 2n-1. But for the new series of the sum of two series, the total number of the series item is of the same order of the term item, i.e. n items of 2n, n-1 items of 2(n-1) n-2 items of 2(n-2), ..., 3 items of 2(3), 2 items of 2(2), 1 items of 2(1). Finally, when all paired terms with equal numbers of items in the two series are added together, the sums of all paired terms are equal to 2n+1. In other words, the sum of two series becomes an arithmetic series with initial term 2n+1 and common difference 2n+1 with the first term equal to 2n+1 and the last term equal to n(2n+1). For an arithmetic series, the sum of the two series is equal to (n(n(2n+1)+(2n+1)))/2=(n(n+1)(2n+1))/2. Since the sum is equal to three original natural number square series, the sum of one natural number squares series is therefore equal to (n(n+1)(2n+1))/6. Imply
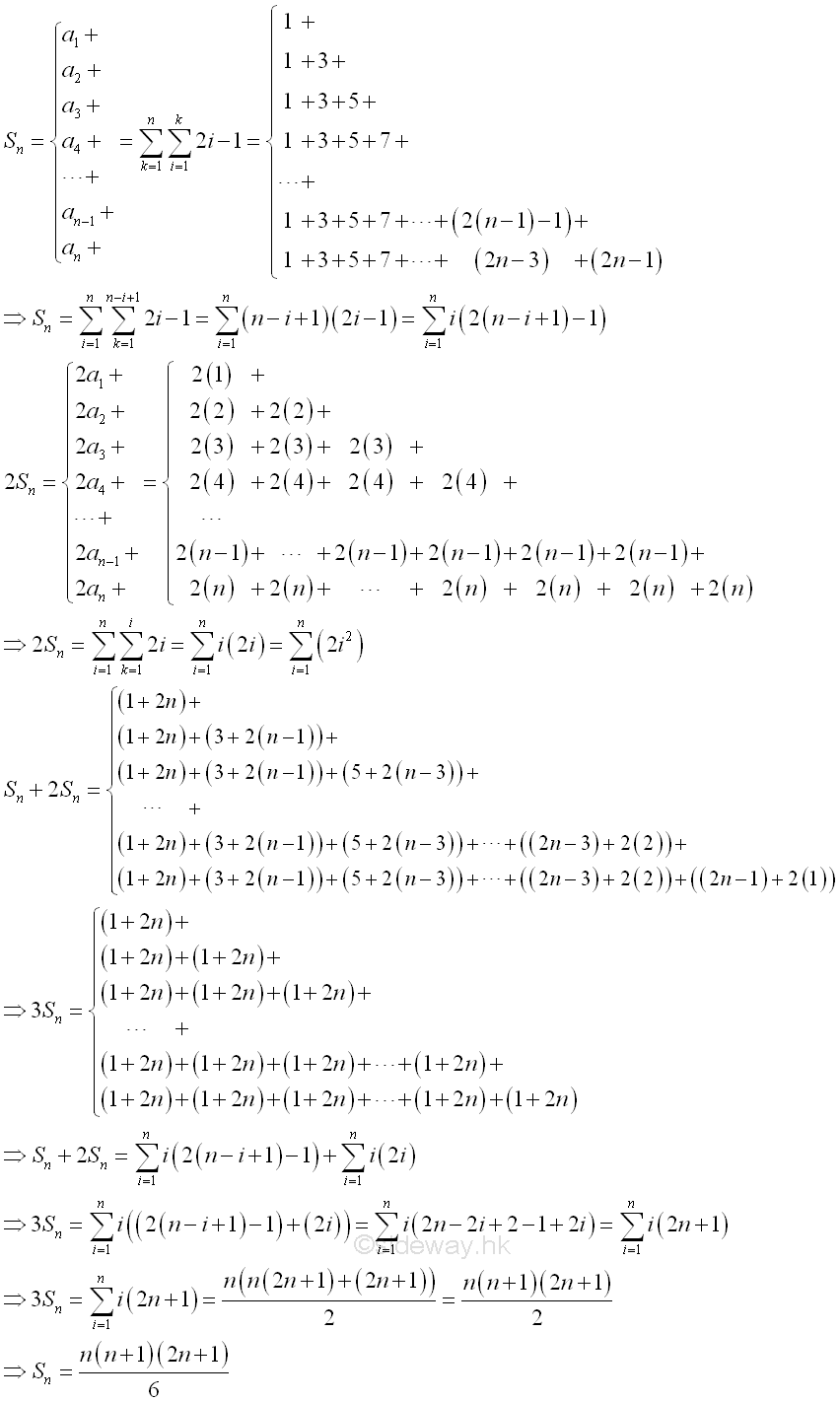
Sequence of First n Natural Number Cubes[1,2]
The sequence of the first n natrual numbers cubes are, 1,
8, 27, ...., or 1,
23, 33, ...., n3. The
first n natural number cubes sequence is an ordered sequence with initial
term equal to 1 and variable difference of two consecutive number squares equal to
k3-(k-1)3 =3k2-3k+1. That is 1, 1+(3(2)2-3(2)+1), 1+(3(2)2-3(2)+1)+(3(3)2-3(3)+1),
1+(3(2)2-3(2)+1)+(3(3)2-3(3)+1)+(3(2)2-3(2)+1),... or 1, 1+7, 1+7+19, 1+7+19+37,...,1+7+19+37+...+(3n2-9n+7)+(3n2-3n+1).
Therefore the general nth term is equal to an=n3=∑ n
i=1(3i2-3i+1).

First n Natural Number Cubes Series[1,2]
As in natural number squares series, since the common difference varies with the term, the sum of the sequence cannot
be determined by the method of finding the sum of an arithmetic series directly.
However, the natural number cubes can also be expressed in a more strategic way
such that the sum of the sequence can be found more easily. Instead of use a
constant initial term, a variable initial term n2-n+1 can also be used so that n3 is equal to the sum of an
arithmetical progression of n terms with common difference, 2. Therefore the
sequence of natural number cubes can be rewritten as 1, 3+5, 7+9+11, 13+15+17+19,...,(n2-n+1)+(n2-n+1)+(n2-n+1)+(n2-n+3)+(n2-n+5)+...+(n2-n+2(n-1)-1)+(n2+n-1). And the general nth term is equal to an=n3= ∑ n
k=1(n2-n+(2k-1)).
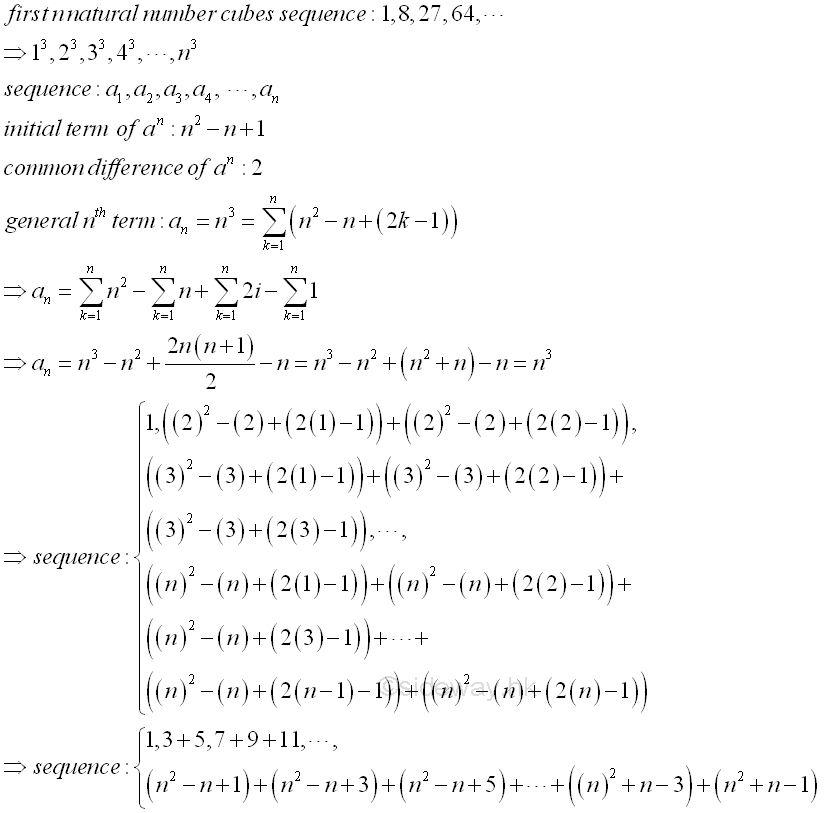
The sequence becomes a triangular arrangement of odd numbers in a regular order.
The ith cube is the sum of i number of consecutive odd
number with initial term equal (i2-i+1)=i(i-1)+1.
Therefore the sum of the natural number cubes series is equal to the sum of
consecutive odd numbers with first term, 1 and last term, (n2+n-1).
The total number of terms in the series is equal to (n(n+1))/2. That is
1+3+5+7+9+11+13+15+17+19+...+(n2+n-3)+(n2+n-1)= ∑ (n(n+1))/2
k=1(2k-1). Since the sum of the natural number cubes series can be
expressed in the form of an arithmetic series, the sum of
natural number cubes is equal to (((n(n+1))/2)((n2+n-1)+1))/2=((n(n+1))/2)((n(n+1))/2)=((n(n+1))/2)2.

©sideway
ID: 130500019 Last Updated: 5/20/2013 Revision: 1 Ref:
References
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
- Wheatstone, C., 1854, On the Formation of Powers from Arithmetical Progressions
- Stroud, K.A., 2001, Engineering Mathematics
- Coolidge, J.L., 1949, The Story of The Binomial Theorem
Latest Updated Links
- Schneider Electric(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)
- Tefal BL83SD PerfectMix Cook Blender(last updated On 11/25/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/24/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/23/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/22/2025)
- Panasonic EH-5282 Hair Dryer(last updated On 11/21/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 53
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
