Content
Trigonometry
Cricular Functions
Reciprocal and Quotient Identities
Reference Acute Angle
The CAST Rule
Negative Angle Identities
Cofunction Identities
Reduction Formulas
Periodicity Identities
General Solutions
Trigonometry
Although trigonometric function is defined based on the right angled triangle, trigonometric functions are usually defined using a unit circle as a circular function.
Cricular Functions
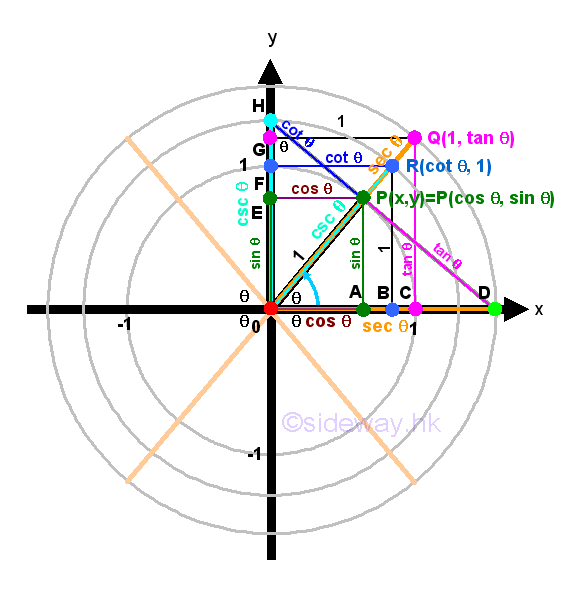
The six trigonometric functions are called circular functions and can be defined by the angle θ in standard position on a Cartesian coordinate system with P(x,y) is the point on the terminal side of the angle θ lied on the unit circle. By right-angled triangle definition, imply the unit circle definition of circular functions are.
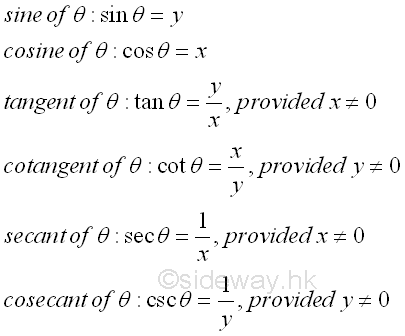
Reciprocal and Quotient Identities
Since point P always moves around the unit circle, point P(x,y) is defined for all θ, therefore both sine and cosine functions are defined for all angles also. As points Q and R are not defined for all θ, therefore tangent, cotangent, secant and cosecant functions are not defined for all angles also. So tangent, cotangent, secant and cosecant functions are usually expressed in terms of consine and sine functions by substituting x=cos θ and y=sin θ into the corresponding expression as the reciprocal and quotient Identities accordingly. Imply
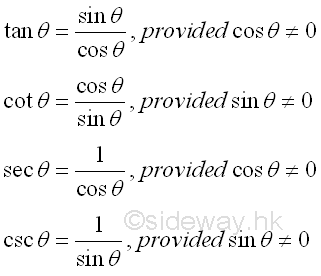
Reference Acute Angle
The symmetric property of unit circle in the cartesian coordinate system can also help to determine circular functions. Regardless, the values of angle θ, any point P(x,y) lies on the terminal side of angle θ and on the unit circle can have another point Q lying on the unit circle by reflecting the original point P about the x-axis, y-axis or origin. For a non-quadrantal angle θ, the acute angle α made between the termianl side of the angle θ and the x-axis is called the reference angle, reference acute angle or related acute angle for θ. Therefore, if angle θ is a quadrant I or IV angle, then angle α is the angle between the terminal side of angle θ and the positive side of x-axis. If angle θ is a quadrant II or III angle, then angle α is the angle between the terminal side of angle θ and the negative side of x-axis. Let angle α be the reference angle for angle θ. Therefore, if the values of the circular functions of an angle exist, the values are of the same as the corresponding circular functions of its reference angle up to a sign. That is cos θ=±cos α, sin θ=±sin α, tan θ=±tan α, cot θ=±cot α, sec θ=±sec α, and csc θ=±css α, and the plus or minus sign depends on the quadrant location of the terminal side of angle θ lies on. In other words, valus of cosine, sine, tangent, cotangent, secant, cosecant functions for angles on quadrant II, III, and IV can be determined by the corresponding reference angle on quadrant I.
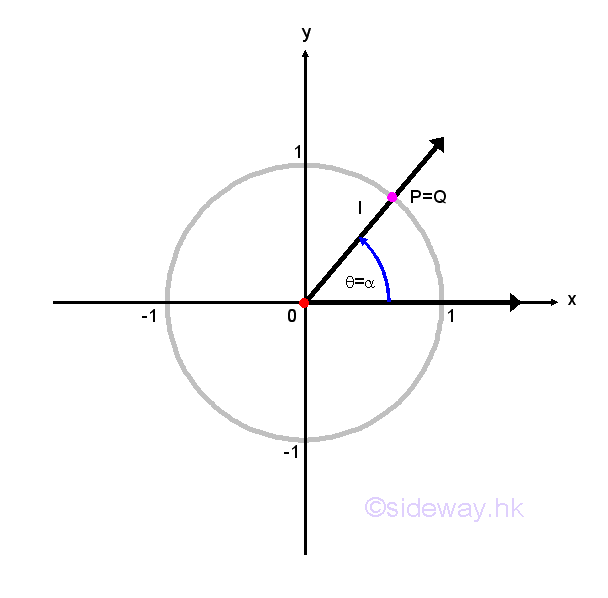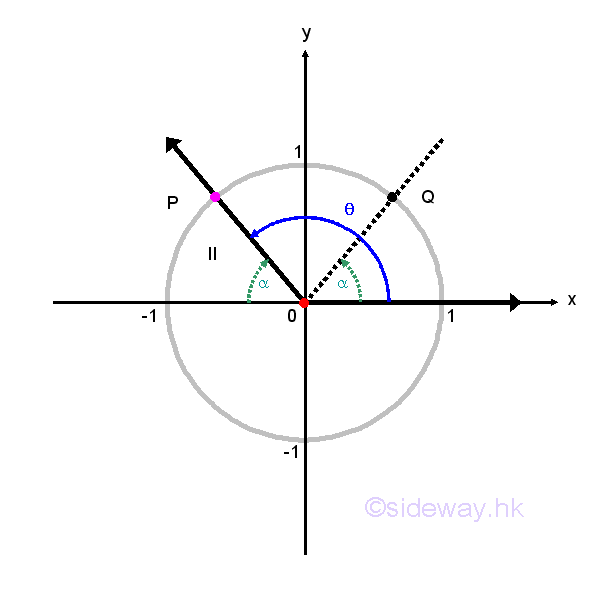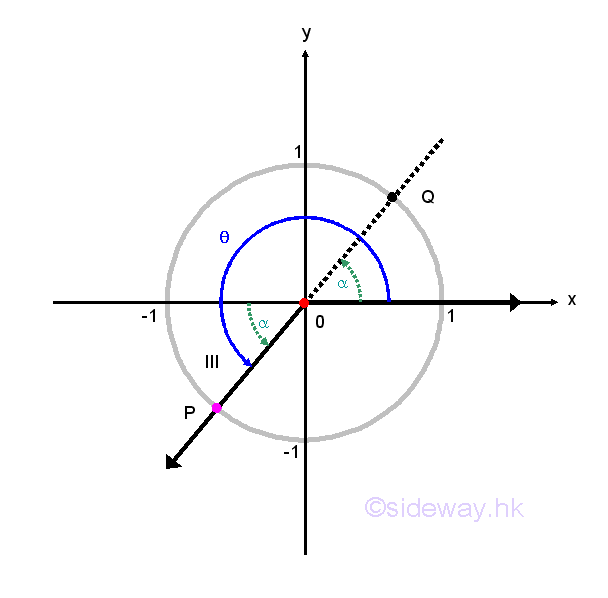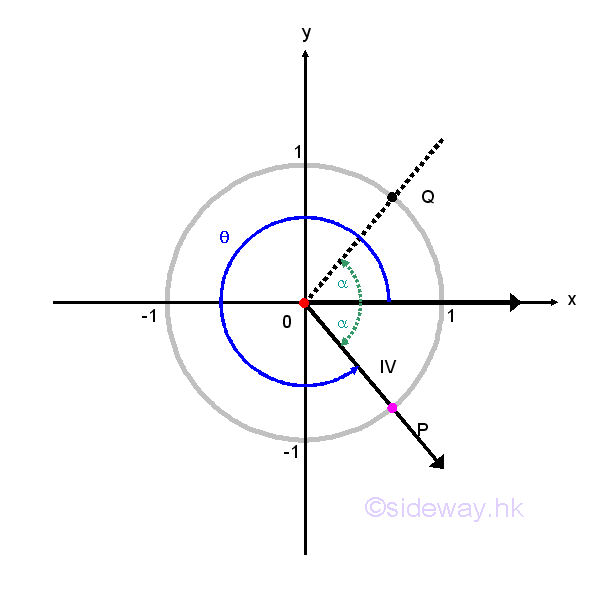
The CAST Rule
Since cosecant function is equal to the reciprocal of sine function for any angles if the value of cosecant function exists, both the cosecant and sine functions should have the same sign. Similarly, the secant function is equal to the reciprocal of cosine function for any angles if the value of secant function exists, both the secant and cosine functions should have the same sign also. For the tangent and cotangent functions, both tangent and cotangent functions are the function of sine and cosine function and are the reciprocal of each other, both the cotangent and tangent functions should have the same sign also. Throught the application of the reciprocal and quotient Identities, the study of trigonometric function properties may focus on the three most important trigonometric function, that is sine, cosine, and tangent functions. The CAST rule is of this type of trigonometric function properties. Since trigonometric functions have different signs in different quadrants of the Cartesian coordinate system. The CAST rule is aided to identify the behaviour of the three basic trigonometric functions in each quadrant. The CAST rule specifies the positive sign of each trigonometric function of the right-angled triangle ratio for any quadrant with an angle in counter-clockwise direction. The acronym CAST stands for "Cosine All Sin Tangent". In first quadrant, the coordinate values of both x and y are positive, therefore sine, cosine and tangent functions of all three trigonometric functions are positive. In second quadrant, the coordinate values of x is negative, while the coordinate values of y is positive, therefore only the cosine function is positive. In third quadrant, the coordinate values of both x and y are negative, therefore only the tangent function is positive. In forth quadrant, the coordinate values of x is positive, while the coordinate values of y is negative, therefore only the cosine function is positive. Instead of starting from the quadrant I with values of all trigonometric functions are positive, the acronym CAST is easy to memorize by starting from the quadrant IV at the lower right corner quadrant with values of cosine functions is positive only.
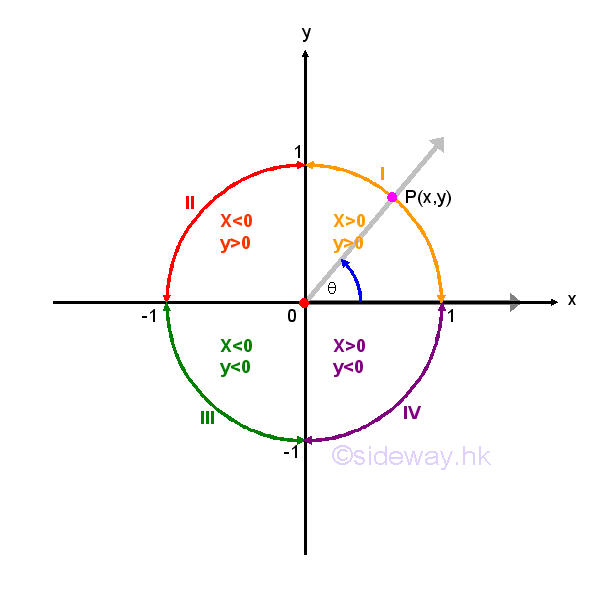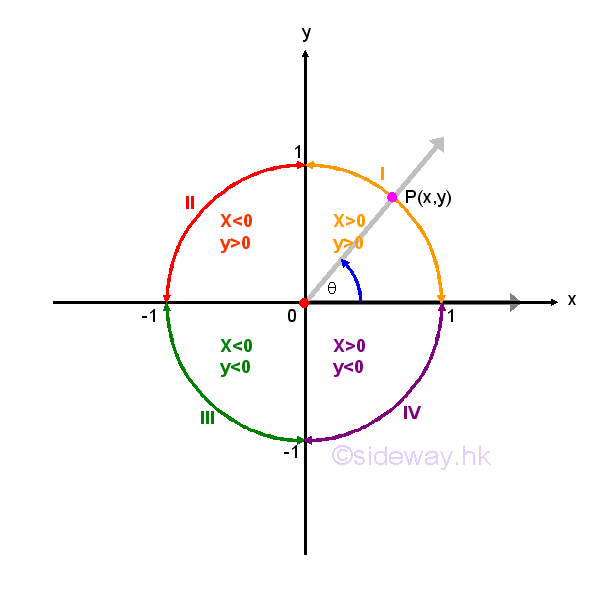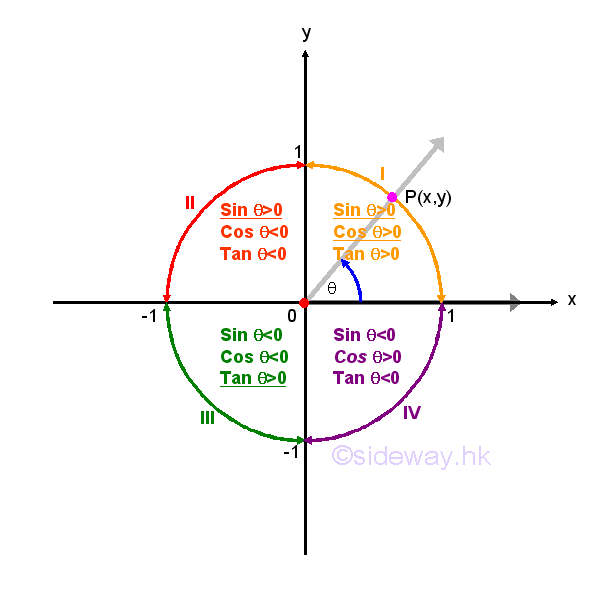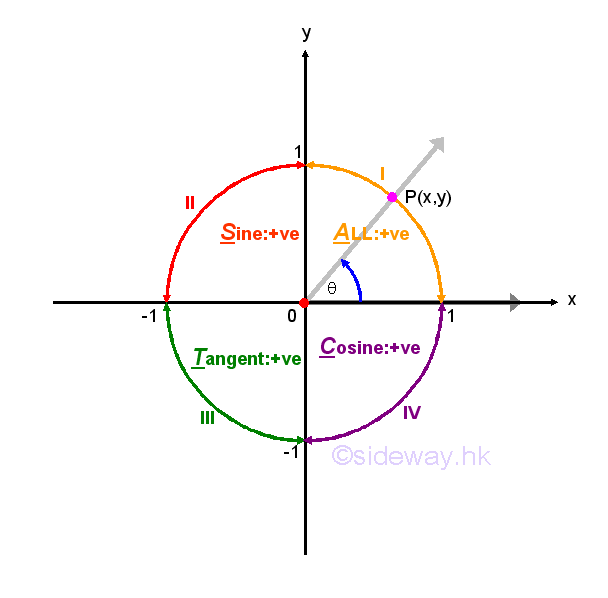
Negative Angle Identities
By definition, a positive angle is generated by a counter-clockwise rotation from the positive x-axis and a negative angle is generated by clockwise rotation from the positive x-axis. But in general, the term negative angle -θ of an angle θ is the angle of same magnitude but opposite in measuring direction from the positive x-axis. For any angle θ in standard position, there is an angle θt of 0≤θt<2π coterminal with θ. Since θ and θt are coterminal angles, the trigonometric functions of two angles are equal. Similarly for negative angles -θ and -θt, angle -θt is also coterminal with angle θ and the trigonometric functions of the two negative angles are equal also. Therefore any angle θ greater then 2π can be reduced to angle of 0≤θt<2π.
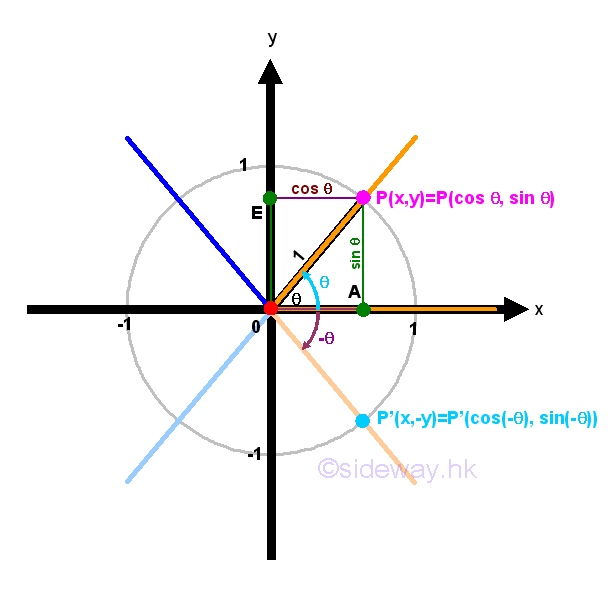
Assuming angle θ is measured in positive counter-clockwise direction, the intersection point between the terminal side of the angle θ and the unit circle is P(x,y). The negative angle -θ can also be found by reflecting the terminal side of the angle θ about the x-axis and the intersection point between the terminal side of the angle -θ and the unit circle becomes P'(x,-y). Therefore according to the unit circle definition of circular functions, sin θ=y; sin(-θ)=-y⇒-sin θ=sin(-θ), cos θ=x; cos(-θ)=x⇒cos θ=cos(-θ), and tan θ=y/x; tan(-θ)=-y/x⇒-tan θ=tan(-θ). By reciprocal and quotient identities, -csc θ=csc(-θ), sec θ=sec(-θ), and -cot θ=cot(-θ). Since the negative angle is obtained by reflecting the terminal side of the angle about the x-axis, these identities also hold when angle θ is measured in negative clockwise direction and for any angles θ. These trigonometric identities are called negative angle identities. Imply

Since the negative angle can be obtained by reflecting the terminal side of the angle about the x-axis, the sign of the trigonometric functions can also be determined by the CAST rule directly. Since values of all trigonometric functions are positive in quadrant 1, therefore only the values of cosine function are positive on both sides of the x-axis. That is when the terminal side of the angle is flipped to other side of the x-axis, the sign of both sine and tangent functions will be switched while the sign of cosine function remains unchanged.
Besides, the negative angle identities can also be used to identify the symmetry of functions. A function f is even if f(-x)=f(x) for every x in the domain of function f. Since for each point P(x,f(x)) of the function f on the Cartesian coordinate system, there exists another point P'(-x,f(-x))=P'(-x,f(x)) on the Cartesian coordinate system also, so that the graph of the function is symmetry about the y-axis, as for each x, the y-coordinate of the plot at x is the same as the y-coordinate of the plot at -x. As value of cosine function cos(-θ) is equal to value of cosine function cos(θ) for all angle θ, cosine function is an even function. A function f is odd if f(-x)=-f(x) for every x in the domain of function f. Since for each point P(x,f(x)) of the function f on the Cartesian coordinate system, there exists another point P'(-x,f(-x))=P'(-x,-f(x)) on the Cartesian coordinate system also, so the graph of the function is symmetry about the origin after rotating 180o or π, as for each x, the y-coordinate of the plot at x is the same as the negative of y-coordinate of the plot at -x. As value of both sine function sin(-θ) and tangent function tan(θ) are equal to the negative value of sine function sin(θ) and tangent function tan(θ) for all angle θ, both sine function and tangent function are odd function. And for tangent function, values of tangent function only exist in the domain of function and tangent function does not exist when θ=π/2+nπ. Similary, by reciprocal and quotient identities, cotangent function is an odd function and values of cotangent function only exist in the domain of function and cotangent function does not exist when θ=nπ. Secant function is an even function and values of secant function only exist in the domain of function and secant function does not exist when θ=π/2+nπ. And cosecant function is an odd function and values of cosecant function only exist in the domain of function and cosecant function does not exist when θ=nπ. Imply
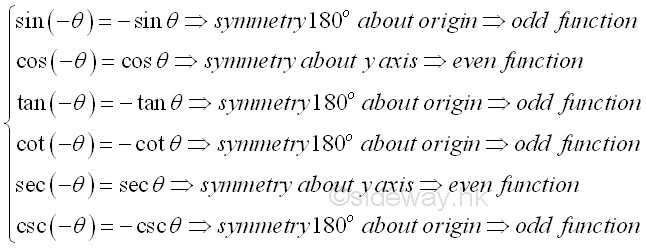
Cofunction Identities
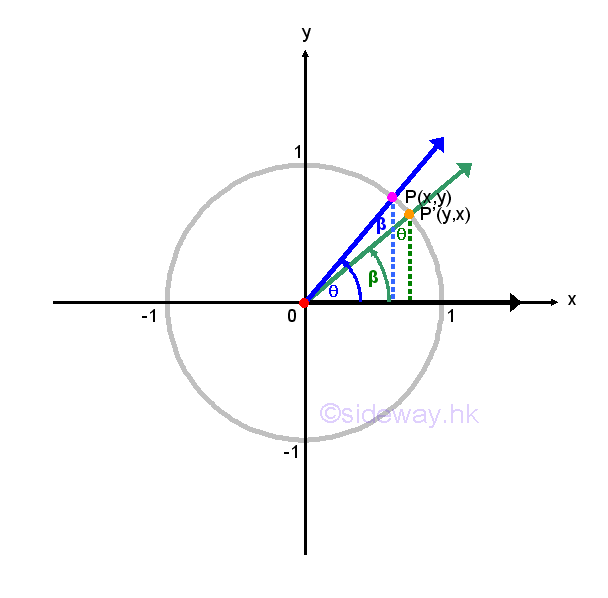
Since the sum of the three angles in a triangle is equal to 180o or π and the right angle of a right angled triangle is already equal to 90o or π/2, the two non-right angles are complementary angles, for example θ and β=π-θ. Using unit circle definition of angle θ, sin θ=y, cos θ=x, tan θ=y/x, cot θ=x/y, sec θ=1/x, csc θ=1/y then by ASA congruent triangles of angle β, sin β=x, cos β=y, tan β=x/y, cot β=y/x, sec β=1/y, csc β=1/x, imply sin β=cos θ=x, cos β=sin θ=y, tan β=cot θ=x/y, cot β=tan θ=y/x, sec β=csc θ=1/y, csc β=sec θ=1/x. Therefore sin(π-θ)=cos θ, cos(π-θ)=sin θ, tan(π-θ)=cot θ, cot(π-θ)=tan θ, sec(π-θ)=csc θ, csc(π-θ)=sec θ. These identities are called cofunction identities. Imply

Reduction Formulas
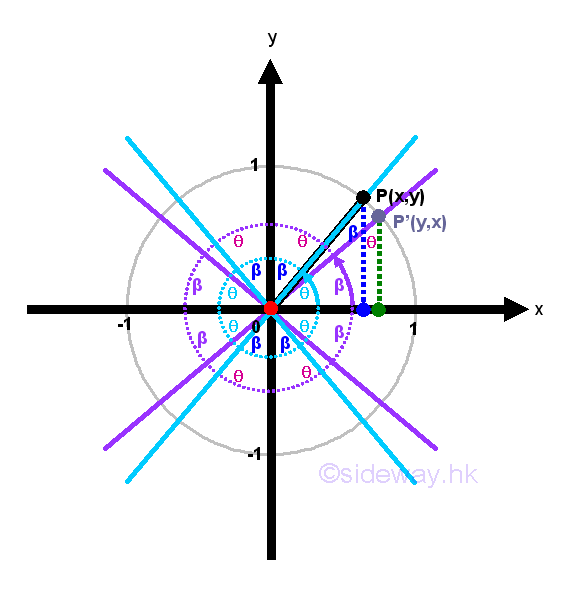
The idea of cofunction identities can further extended from π/2 to other typical angles using fundamental identities to express trigonometric functions of similar typical angles in terms of θ only, where θ is an acute angle. These formulas are called reduction formulas. Since θ is always an acute angle, the reference acute angle together with cofunction identities and the CAST rule can be used to simplify these typical angles. For angle π/2-θ, that is the cofuntion identities. For angle π/2+θ, the angle is in quadrant II, and the reference acute angle is equal to π-(π/2+θ)=π/2-θ. For angle π-θ, the angle is in quadrant II, and the reference acute angle is equal to π-(π-θ)=θ. For angle π+θ, the angle is in quadrant III, and the reference acute angle is equal to (π+θ)-π=θ. For angle 3π/2-θ, the angle is in quadrant III, and the reference acute angle is equal to (3π/2-θ)-π=π/2-θ. For angle 3π/2+θ, the angle is in quadrant IV, and the reference acute angle is equal to 2π-(3π/2+θ)=π/2-θ. Since values of trigonometric functions is repeated every 2π, 2π is usually represented by 2nπ. For angle 2nπ-θ or -θ, the angle is in quadrant IV, and the reference acute angle is equal to 2nπ-(2nπ-θ)=θ. For angle 2nπ+θ or θ, the angle is in quadrant I, and the reference acute angle is equal to (2nπ+θ)-2nπ=θ. Imply
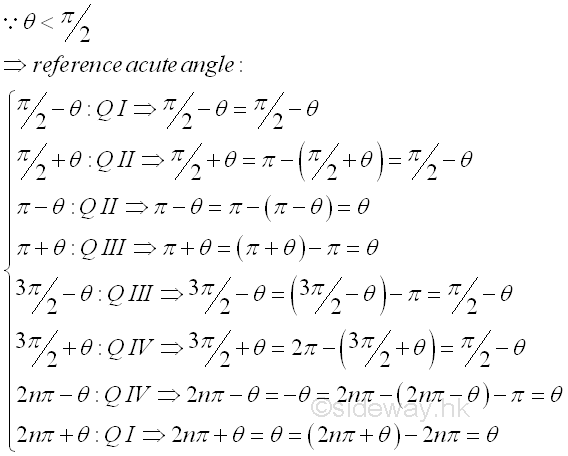
Since the simplified angles can be grouped into (π/2-θ) and θ, both the cofunction identities and CAST rules are needed to tranform trigonometric functions of these typical angles into simple angle θ only. For sine function, sin(π/2-θ)=sin(π/2-θ) in Q I and is equal to cos θ by cofunction identity. And sin(π/2+θ)=sin(π/2-θ) in Q II and is equal to cos θ by cofunction identity. And sin(π-θ)=sin θ in Q II. And sin(π+θ)=-sin θ in Q III. And sin(3π/2-θ)=-sin(π/2-θ) in Q III and is equal to -cos θ by cofunction identity. And sin(3π/2+θ)=-sin(π/2-θ) in Q IV and is equal to -cos θ by cofunction identity. And sin(2nπ-θ)=sin(-θ)=-sin θ in Q IV. And sin(2nπ+θ)=sin(θ)=-sin θ in Q I. For cosine function, cos(π/2-θ)=cos(π/2-θ) in Q I and is equal to sin θ by cofunction identity. And cos(π/2+θ)=-cos(π/2-θ) in Q II and is equal to -sin θ by cofunction identity. And cos(π-θ)=-cos θ in Q II. And cos(π+θ)=-cos θ in Q III. And cos(3π/2-θ)=-cos(π/2-θ) in Q III and is equal to -sin θ by cofunction identity. And cos(3π/2+θ)=cos(π/2-θ) in Q IV and is equal to sin θ by cofunction identity. And cos(2nπ-θ)=cos(-θ)=cos θ in Q IV. And cos(2nπ+θ)=cos(θ)=cos θ in Q I. For tangent function, tan(π/2-θ)=tan(π/2-θ) in Q I and is equal to cot θ by cofunction identity. And tan(π/2+θ)=-tan(π/2-θ) in Q II and is equal to -cot θ by cofunction identity. And tan(π-θ)=-tan θ in Q II. And tan(π+θ)=tan θ in Q III. And tan(3π/2-θ)=tan(π/2-θ) in Q III and is equal to cot θ by cofunction identity. And tan(3π/2+θ)=-tan(π/2-θ) in Q IV and is equal to -cot θ by cofunction identity. And tan(2nπ-θ)=-tan(-θ)=tan θ in Q IV. And tan(2nπ+θ)=-tan(θ)=tan θ in Q I. Imply

And cotangent, secant and cosecant functions can then be obtained by reciprocal and quotient identities accordingly.. Imply
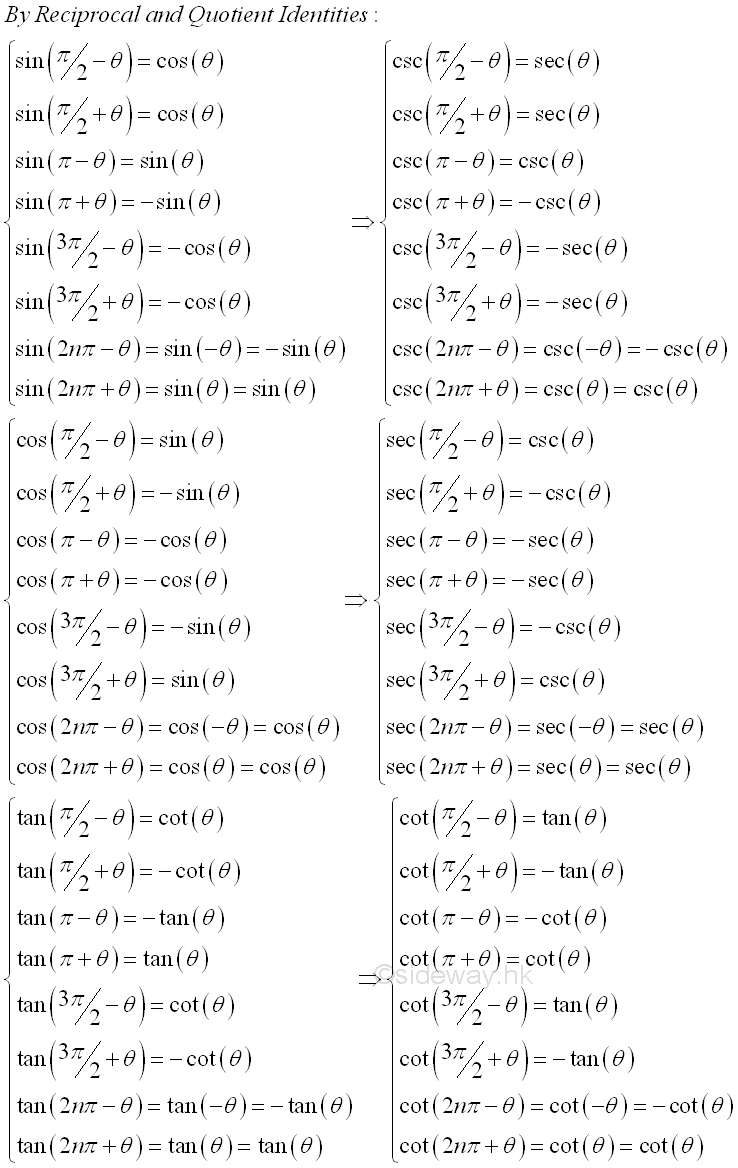
The reduction formulas is summerized as following:
| a | sin | cos | tan | cot | sec | csc | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Radians | α-θ | α+θ | α-θ | α+θ | α-θ | α+θ | α-θ | α+θ | α-θ | α+θ | α-θ | α+θ |
| 0 | -sin θ | sin θ | cos θ | cos θ | -tan θ | tan θ | -cot θ | cot θ | sec θ | sec θ | -csc θ | csc θ |
| π/2 | cos θ | cos θ | sin θ | -sin θ | cot θ | -cot θ | tan θ | -tan θ | csc θ | -csc θ | sec θ | sec θ |
| π | sin θ | -sin θ | -cos θ | -cos θ | -tan θ | tan θ | -cot θ | cot θ | -sec θ | -sec θ | csc θ | -csc θ |
| 3π/2 | -cos θ | -cos θ | -sin θ | sin θ | cot θ | -cot θ | tan θ | -tan θ | -csc θ | csc θ | -sec θ | -sec θ |
| 2πn | -sin θ | sin θ | cos θ | cos θ | -tan θ | tan θ | -cot θ | cot θ | sec θ | sec θ | -csc θ | csc θ |
Periodicity Identities
From unit circle definition of trigonometric functions, values of trigonometric functions is repeated every 2π, therefore, in general, trigometric functions have the periodic property of 2π. More information can also be obtained from the unit circle to provide a general idea on the values of trigonometric function in an interval. In the first quadant, sine function is increasing, cosine function is decreasing and tangent functions is increasing also. Besides, the periodic properties of trigonometric functions can also be determined by the reduction formulas. For the sine function, the equivalent values from reduction formulas in the four quadrants with reference angles of interval π/2, are sin θ, cos θ, -sin θ, and -cos θ. The value of sine function is repeated every 2π. As sin(-θ)=-sin θ, let θ be acute angles between -π/2 to π/2. Let n=0,1,2,..., then the angle of sine function can be expressed as θ=2πn+θ. For the cosine function, the equivalent values from reduction formulas in the four quadrants with reference angles of interval π/2, are cos θ, -sin θ, -cos θ, and sin θ. The value of cosine function is repeated every 2π. As cos(-θ)=cos θ, let θ be acute angles between -π/2 to π/2. Let n=0,1,2,... then the angle of cosine function can be expressed as θ=2πn+θ. For the tangent function, the equivalent values from reduction formulas in the four quadrants with reference angles of interval π/2, are tan θ, -cot θ, tan θ, and -cot θ. The value of tangent function is repeated every π instead of 2π. As tan(-θ)=-tan θ, let θ be acute angles between -π/2 to π/2. Let n=0,1,2,..., then the angle of tangent function can be expressed as θ=πn+θ. By reciprocal and quotient identities, Imply the angle of cotangant function can be expressed as θ=πn+θ, the angle of secant function can be expressed as θ=2πn+θ, and the angle of cosecant function can be expressed as θ=2πn+θ, Imply

General Solutions
Although the periodicity identities of trigonometry functions have already shown the general solutions of trigonometric functions, there is another way to elaborate the periodicity of trigonometric functions for any given angle ɸ, not necessary an acute angle. For the sine function, considering two quadrants as a group, the absolute values of a sine function is repeated every π with sign changed only. Consider another set of refernece acute angle in quadrants by reduction formulas, with reference angles of interval π , that is sin θ, sin θ, -sin θ, and -sin θ. As sin(-θ)=-sin θ, the set of referenc angles can be rewritten as sin θ, sin θ, sin(-θ), and sin(-θ). Since interval of paired angles in two quadrants interval is equal to π and sign is changed between two intervals, any given angle ɸ can therefore be expressed as ɸ=πk+(-1)kα, where k=0,1,2,... and α:-π/2<α<π/2. For the cosine function, considering two quadrants as a group, the absolute values of a cosine function is repeated every π with sign changed only. Consider another set of refernece acute angle in quadrants by reduction formulas, with reference angles of interval π , that is cos θ, -cos θ, -cos θ, and cos θ. As cos(-θ)=cos θ, the set of referenc angles can not be rewritten in term of interval π, however cos(-θ)=cos θ guarantees that values of cosine function are equal in both positive and negative angle with interval 2π. Since an angle can be either positive or negative, the range of angle in the interval 2π can also be reduced to π, any given angle ɸ can therefore be expressed as ɸ=2πk±β, where k=0,1,2,... and θ:-π<β<π. For the tangent function, considering two quadrants as a group, the values of a tangent function is repeated every π. Consider another set of refernece acute angle in quadrants by reduction formulas, with reference angles of interval π , that is tan θ, -tan θ, tan θ, and -tan θ. As tan(-θ)=-tan θ, the set of referenc angles can be rewritten as tan θ, tan(-θ), tan θ and tan(-θ). Since interval of paired angles in two quadrants interval is equal to π and the sign is remained unchanged between two intervals, any given angle ɸ can therefore be expressed as ɸ=πk+α, where k=0,1,2,... and α:-π/2<α<π/2. By reciprocal and quotient identities, Imply any angles of cotangant function can be expressed as ɸ=πk+α, where k=0,1,2,... and α:-π/2<α<π/2, any angles of secant function can be expressed as ɸ=2πk±β, where k=0,1,2,... and θ:-π<β<π, and any angles of cosecant function can be expressed as ɸ=πk+(-1)kα, where k=0,1,2,... and α:-π/2<α<π/2, Imply

©sideway
ID: 130600003 Last Updated: 6/6/2013 Revision: 1 Ref:
References
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
- Ayres, F. JR, Moyer, R.E., 1999, Schaum's Outlines: Trigonometry
- Hopkings, W., 1833, Elements of Trigonometry
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
