Content
Kinematics:
One Dimension
Position
Displacement
Velocity
Average Velocity
Instantaneous Velocity
Acceleration
Average
Acceleration
Instantaneous Acceleration
Kinematics: One Dimension
Kinematics is the study of the geometry of an object's motion which is related to the position, velocity, and acceleration with respect to time. In the simple case, an object, which can be represented by a particle, when the motion of the motion is to be considered as one single unit and the rotation about the mass centre of the object can be neglected. In one dimension, an object moving along a straight line is called linear motion. Sometimes, a linear motion is called rectilinear motion. Since there is only one dimension, the vector direction is fixed and only the sense and magnetude of a vector quantity are needed to be specified. As the object is only shifted from one point to another, the object is under a translational motion.
Position
The position of an object is used to specify where the object is when describing the motion of the object. For one dimension, a number line with measurement unit is used to locate the position of an object. Although there is no limitation on the orientation of the number line, i.e. the motion can be neither vertical or horizontal, but in general, the positive direction of a number line is increasing from left to right or from down to up with the origin at point zero 0. As the position of an object can only be on the either side of the origin and there is only one direction, the vector quantity can be reduced to sense and magnitude. The position of an object is then the distance measured from the origin O to the position of the object along the number line with a plus or minus sign to indicate the movement along the number line in the positive or the negative direction. The value of distance used to define the position of the object is called the position coordinate of the object. The SI unit of the position measurement is meter (m).
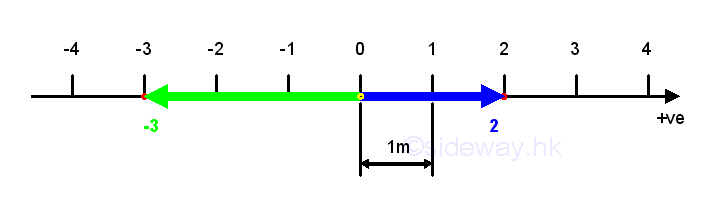
Displacement
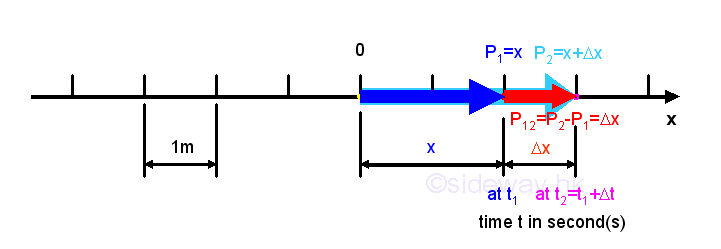
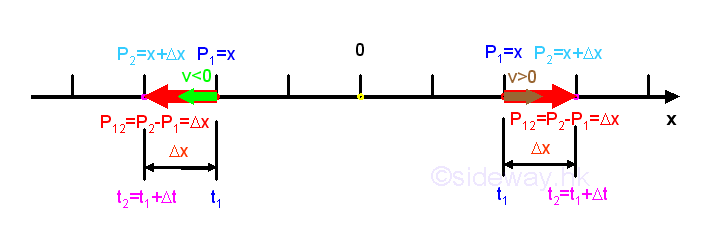
The displacement of an object is the linear distance measured from the initial original position P1 to the final destination position P2 with plus sign indicating the positive movement of the object and minus sign indicating the negative movement direction along the number line. The value of displacement of the object is therefore equal to the position coordinate of the object at the final position minus the position coordinate of the object at the initial position. For example, positve motion P12 =P2-P1=Δx. For one dimensional linear motion of an object, the distance measurement is equal to the distance measurement. The SI unit of the displacement measurement is meter (m).
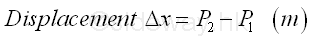
Velocity
Velocity is used to describe how fast the object is moving with direction. And the direction and of the velocity are always same as the direction of displacement.
Average Velocity
By definition, the average velocity of an object over the considered period or time interval is equal to the displacement of the object in the time interval from the initial position to the final position, that is P12 =P2-P1=Δx, over the period of time interval, t2-t1=Δt. In other words, average velocity is the rate of change of position with respect to time over the considered period. The SI units of the average velocity measurement are meter (m) for the displacement measurement and second (s) for the time measurement and is equal to m/s.
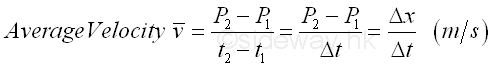
In general, the direction of the velocity vector is same as the direction of the displacement vector. If P2>P1, then the value of velocity v is positive which indicates that position x is increasing, or the object moves in the positive direction and the velocity is in positive direction also. If P2<P1, then the value of velocity v is negative which indicates that position x is decreasing, or the object moves in the negative direction and the velocity is in negative direction also. Therefore the number of value of velocity is the magnitude of the velocity vector while the sign of value of velocity is the sense of the velocity vector.
Instantaneous Velocity
The instantaneous velocity of an object is defined as the velocity of the object at a particular instant time of interest. From the average velocity, as the time interval becomes shorter and shorter, the displacement will becomes shorter and shorters also. When these measurements are small enough, there always exist an average velocity such that the average velocity can be used to approximate the velocity of the object over the considered time interval. In other words, when the time interval Δt approaching zero, the final position of the object will more close to the initial position and the rate of change of position with respect to time, that is v, approaching constant also, the instantaneous velocity or the rate of change of the position at a particular instant can then be approximated by the average velocity over the infinitely small time interval. The SI units of the instantaneous velocity measurement are meter (m) for the displacement measurement and second (s) for the time measurement as in average velocity. The sense of the instantaneous velocity vector is also indicated by the sign of the instantaneous velocity. And the number of value of instantaneous velocity is the magnitude of the instantaneous velocity vector, and is sometimes called the speed of the object.
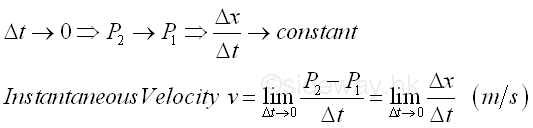
From calculus, by the definition of derivative, the rate of change of
position x with respect to time t when taking limit as Δt approaching 0 is
equal to the derivative of the positon function with respect to time. Imply 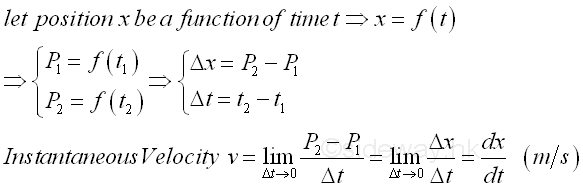
Acceleration
Acceleration is used to describe how the velocity of an object changes with time. In general, the changes can be any combination of change direction, speed up and slow down. And the sense and direction of the acceleration is equal to the vector difference of final velocity vector minus initial velocity vector. In one dimension, the velocity vectors of an object are always of same direction but may have different senses and magnitudes.
Average Acceleration
By definition, the average acceleration of an object over the considered period or time interval is equal to the change of the velocities of the object in the time interval from the initial position to the final position over the period of time interval. In other words, average avveleration is the rate of change of velocity with respect to time over the considered period. The SI units of the average acceleration measurement are meter/second (m/s) for the velocity measurement and second (s) for the time measurement and is equal to m/s-2.
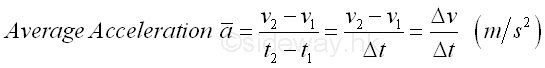
In one dimenstion motion, there is no change of direction in velocity. and therefore the direction of the acceleration vector is same as the direction of the veloctiy vectors. If v2>v1, then the value of acceleration a is positive which indicates that velocity v is increasing, or the object moves faster in the positive direction and the acceleration is in positive direction also. If v2<v1, then the value of acceleration a is negative which indicates that velocity v is decreasing, or the object moves faster in the negative direction and the acceleration is in negative direction also. Therefore the number of value of acceleration is the magnitude of the acceleration vector while the sign of value of acceleration is the sense of the acceleration vector.
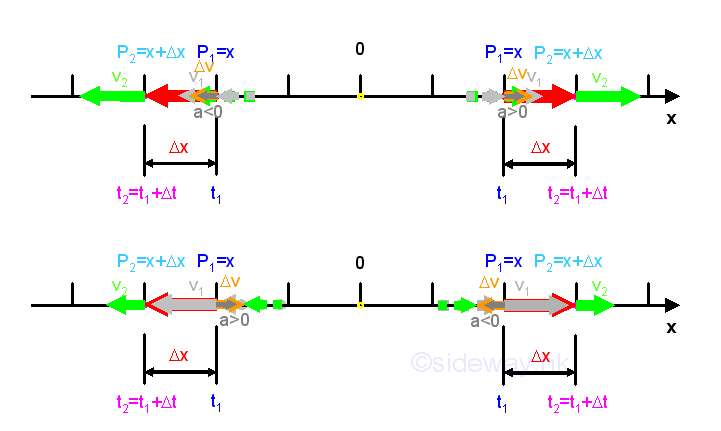
Since acceleration a is used to describe both the direction and magnetude of how the velocity of an object changes with time, the acceleration vector is always reference to the initial velocity vector also. The magnetude of the velocities along the motion of an object may be increasing or decreasing. Sometimes, the term deceleration is used to refer to acceleration a when the speed or the magnetude of velocity of the object is decreasing along the motion.
Instantaneous Acceleration
The instantaneous acceleration of an object is defined as the acceleration of the object at a particular instant time of interest. From the average acceleration, as the time interval becomes shorter and shorter, the displacement will becomes shorter and shorters also. When these measurements are small enough, there always exist an average acceleration such that the average acceleration can be used to approximate the rate of change of the velocity of the object over the considered time interval. In other words, when the time interval Δt approaching zero, the final position of the object will more close to the initial position and the rate of change of velocity with respect to time, that is a, approaching constant also, the instantaneous acceleration or the rate of change of the velocity at a particular instant can then be approximated by the average acceleration over the infinitely small time interval. The SI units of the instantaneous acceleration measurement are meter/second (m/s) for the velocity measurement and second (s) for the time measurement as in average acceleration. The sense of the instantaneous acceleration vector is also indicated by the sign of the instantaneous acceleration. And the number of value of instantaneous acceleration is the magnitude of the instantaneous acceleration vector.
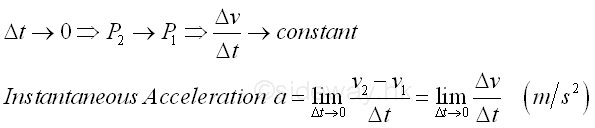
From calculus, by the definition of derivative, the rate of change of
velocity v with respect to time t when taking limit as Δt approaching 0 is
equal to the derivative of the velocity function with respect to time. Imply
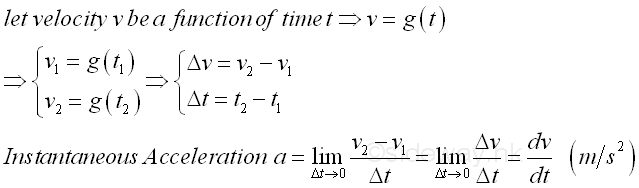
Since velocity v is also a function of time t. Imply
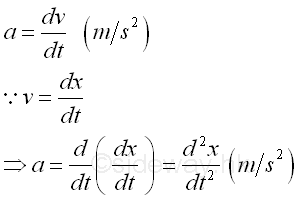
©sideway
ID: 140200005 Last Updated: 2/5/2014 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 37
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
