Logarithm TheoremPythagorean TheoremCombinatoricsQuadratic EquationsSequence and SeriesLinear AlgebraDiophantine EquationElliptic CurveAlgebra Result
Draft for Information Only
Content
Pythagorean Triples
Algebraic Approach
Higher Degree
Source and Reference
Pythagorean Triples
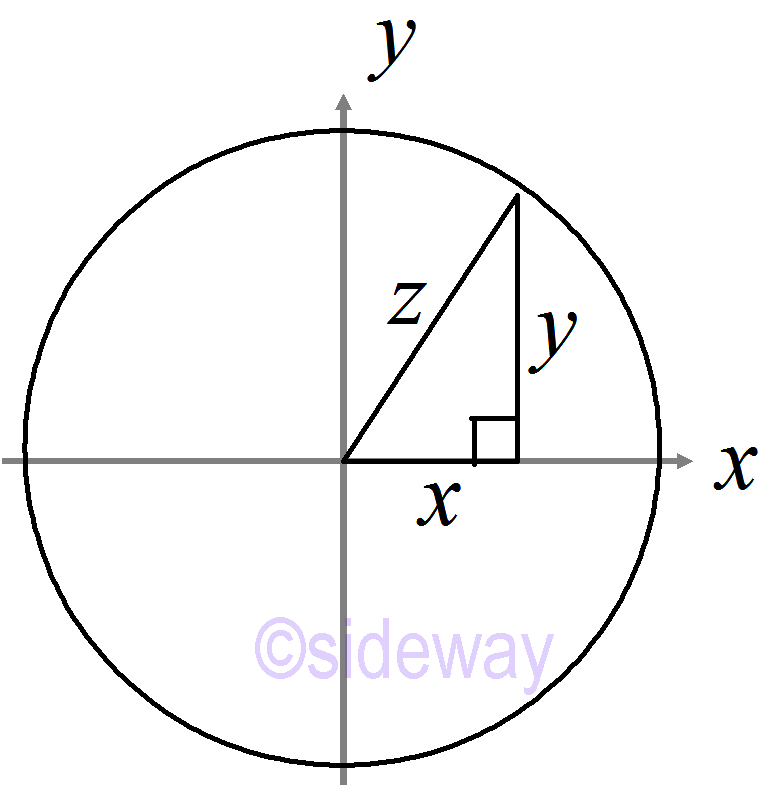 Pythagorean Triples: 𝑥2+𝑦2=𝑧2
Pythagorean Triples: 𝑥2+𝑦2=𝑧2If 𝑧≠0,
𝑥𝑧
𝑦𝑧
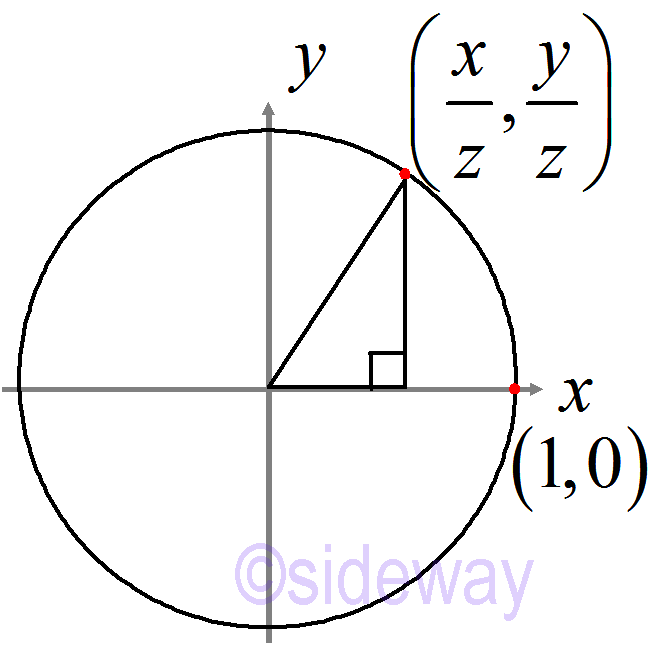
Algebraic Approach
ℚ(𝑖)={𝑎+𝑏𝑖;𝑎,𝑏∊ℚ} is a field of number system that build the structure to the rational solutions of 𝑥2+𝑦2=1⇒𝑥2+𝑦2=(𝑥+𝑦𝑖)(𝑥−𝑦𝑖)=1 ⇒(𝑥+𝑦𝑖)2(𝑥−𝑦𝑖)2=1 rasie to higher power ⇒((𝑥2−𝑦2)+(2𝑥𝑦)𝑖)((𝑥2−𝑦2)−(2𝑥𝑦)𝑖)=1 ⇒(𝑥2−𝑦2)2+(2𝑥𝑦)2=1 structure of the equation is still preserved ⇒𝑥4+𝑦4+2𝑥2𝑦2=1 Similarly, (𝑥2+𝑦2)2=1⇒𝑥4+𝑦4+2𝑥2𝑦2=1
Solutions to the equation are
,35,45
−,725,2425
−,5276255,−336625
, ⋯164833390625,354144390625
The solutions to the equation can be expanded by combining more than one set of solutions through binary operation.
{
and35,45
⇒1213,513
1665,6365
and1665,6365
⇒35,45
−That is 𝑍={(𝑥,𝑦)∊ℚ2:𝑥2+𝑦2=1} 𝑃(𝑥,𝑦),𝑄(𝑤,𝑧)∊𝑍⇒𝑃⊕𝑄∊𝑍, 𝑃⊕𝑄=(𝑥𝑧−𝑦𝑤),(𝑥𝑤+𝑦𝑧)) For binary operation:204325,253325
- 𝑃⊕𝑄=𝑄⊕𝑃
- (𝑃⊕𝑄)⊕𝑅=𝑃⊕(𝑄⊕𝑅)
- 𝐸=(1,0)⇒𝐸⊕𝑃=𝑃
Higher Degree
Similar to second degree,Suppose (𝑥+𝑦∛2+𝑧∛22)(𝑥+𝑦∛2𝜁+𝑧∛22𝜁2)(𝑥+𝑦∛2𝜁2+𝑧∛22𝜁)=1
Let 𝜁3=1 and 𝜁2+𝜁+1=0, and 𝜁4= 𝜁3𝜁1=𝜁
⇒𝑥3+2𝑦3−6𝑥𝑦𝑧+4𝑧3=1
⇒{(𝑥,𝑦,𝑧)}∊ℚ3:𝑥3+2𝑦3−6𝑥𝑦𝑧+4𝑧3=1}
For Higher Power
(𝑥+𝑦∛2+𝑧∛22)n=2,3⇒𝑥'+𝑦'∛2+𝑧'∛22
(𝑥+𝑦∛2𝜁+𝑧∛22𝜁2)n=2,3⇒𝑥'+𝑦'∛2𝜁+𝑧'∛22𝜁2
By raise the equation to power of 2
(𝑥+𝑦∛2+𝑧∛22)2(𝑥+𝑦∛2𝜁+𝑧∛22𝜁2)2(𝑥+𝑦∛2𝜁2+𝑧∛22𝜁)2=1
⇒(𝑥'+𝑦'∛2+𝑧'∛22)(𝑥'+𝑦'∛2𝜁+𝑧'∛22𝜁2)(𝑥'+𝑦'∛2𝜁2+𝑧'∛22𝜁)=1
⇒𝑥'3+2𝑦'3−6𝑥'𝑦'𝑧'+4𝑧'3=1
where {
𝑥'=𝑥2+4𝑦𝑧𝑦'=𝑦2+2𝑥𝑧𝑧'=2𝑥𝑦+2𝑧2
Source and Reference
https://www.youtube.com/watch?v=nS6YwdKIIKAhttps://www.youtube.com/watch?v=ABr3QisSAWQ
©sideway
ID: 201100015 Last Updated: 11/15/2020 Revision: 0 Ref:
References
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
- Wheatstone, C., 1854, On the Formation of Powers from Arithmetical Progressions
- Stroud, K.A., 2001, Engineering Mathematics
- Coolidge, J.L., 1949, The Story of The Binomial Theorem
Latest Updated Links
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Imbiah(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 36
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
