Content
Calculus
Functions and Models
Limits and Continuity of Functions
Instantaneous
Rate of Change
Instantaneous Effect
Derivatives and integrals
Calculus
Calculus is a mathematical tool focused on functions, limits, and the instantaneous change.
Functions and Models
A function f can be defined as the correspondence or relationship between two sets, X and Y. In which, each element x of X is assigned to a unique element y of Y. The set X is the domain of the function and the set Y is the range of the function. The elements x of set X is called arguments of the function and the elements y of set Y is called values of the function of x. Or element y is the image of x under function f. That is
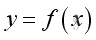
A model or mathematical model is usually used to decribe a problem by means of a function or in the form of mathematical equations. for example
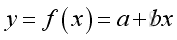
The element symbol x in the domain of the function f is called an independent variable. The element symbol y in the range of the function is called a dependent variable and its value depends on the value of the assigned independent variable.. Both symbols x and y are variables of the equation and are related by a function of f. The symbols, a and b are fixed values or constants of the function
Limits and Continuity of Functions
Limits of a function is an important fundamental concept in calculus. Limit is the value f(x) of a function f when x is getting very close to a number a. The limit, or the value f(x) approaching a, is not necessarily equal to the value f(a) of the function when x=a.
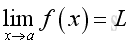
When number a is defined in the domain and the limit of the function f exist, the function is said to be continuous at x=a if the limit of the function f , when x approaching a is equal to the value of function at a. Otherwise the function f is discontinuous at a.
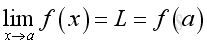
In calculus, the most important points of interest is the value f(x) of a function f when x approaching a number a.
Instantaneous Rate of Change
For example, the average speed v of an object is the average of the travelled distance d of an object in a given time interval t. Imply
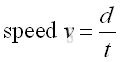
If the average speed is considered as a small interval of the whole travelled distance over a small interval of the period of time travel.
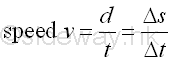
In other words, average speed is a rate or a rate of change and can also be considered as the speed over the period of the time travelled. However, the deviation between the average speed and the fastest speed or the slowest speed may be large when the time interval is large. Therefore the average speed cannot be used to represent the actual speed at a specific point of time. The accuracy of the average speed can be improved by reducing the period of time travelled. As the period of time travelled equal to zero, the calculated average speed shoud equal to the actual velocity at the specific point of time. Imply
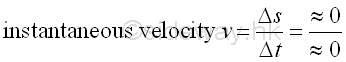
Mathematicallty, the quotient of Δs divided by Δt can be any real number. By making use of the limit concept, the instantaneous velocity v can be approximated by reducing the time travelled close to zero. And the instantaneous velocity v at a specific point of time a is
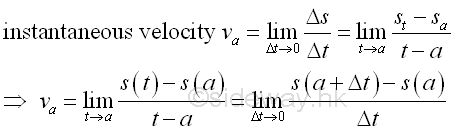
This method is widely used to calculate the instantaneous rate of change of quantity function with respect to an infinitely small interval variable quantity at a specific variable point in practical application. The instantaneous velocity is the derivative of travelled distance with respect to time travelled. The process of finding a derivative is called differentiation
Instantaneous Effect
The instantaneous travelled distance Δs of an object at a specific point of time a over an infinitely small time interval is equal to the instantaneous veloctiy v of an object at the specific point of time a times the infinitely small time interval Δt. Imply
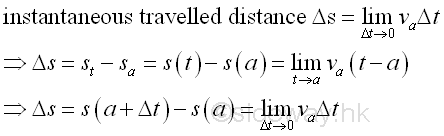
In other words, the instantaneous travelled distance can be considered as the instantaneous effect of the instantaneous rate of change or instantaneous velocity over a period of an infinitely small time interval Δt at a specific point of time.
Area calculation is one of the most common applications of using this instantaneous effect. For example, the area of a circle can be approximated by the area of inscribed regular polygon without the using of pi. The area of the regular polygon of n sides inscribed in a circle is always smaller than the area of the circle but when n approaches infinity, the area of the inscribed regular polygon of n sides should approach to the area of the circle also. The inscribed regular polygon of n sides can be divided into n number of isosceles triangles. The area of isosceles triangle of inscribed regular polygon can be easily determined in terms of the sides of the regular polygon.
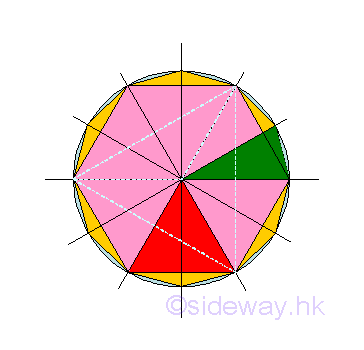
When the number of sides of the polygon approaches infinity, the vertex angle approaches zero. The instantaneous effect is the infinitely small triangular area over a infinitely small angle. And the area of a circle is therefore equal to the summation of all infinitely small triangular area over the region from 0 to 360 degree. Since the base and height of the isosceles triangle is also changed with the vertex angle of the isosceles triangle, the area of the isosceles triangle can be determined by the base and height of the isosceles triangle. And the area of the regular polygon of n sides is equal to n times the area of the isosceles triangle.
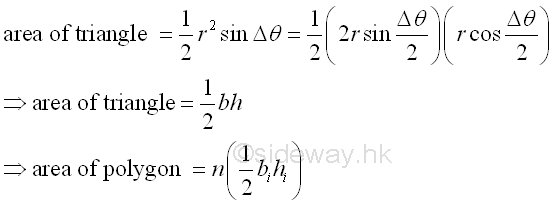
The base and height of the isosceles triangle is.
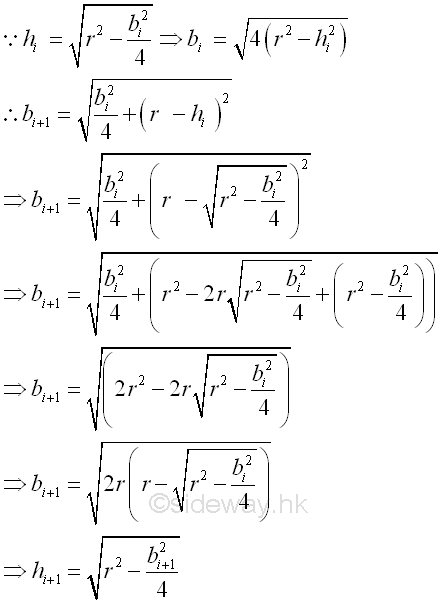
When number of sides n is equal to 3, h=0.5r, imply

Therefore the area of a circle is approximately equal to πr2 when the number of sides of a polygon is more than 12. And the area of a circle is therefore equal to the summation of all infinitely small triangular area over the region from 0 to 360 degree. Imply
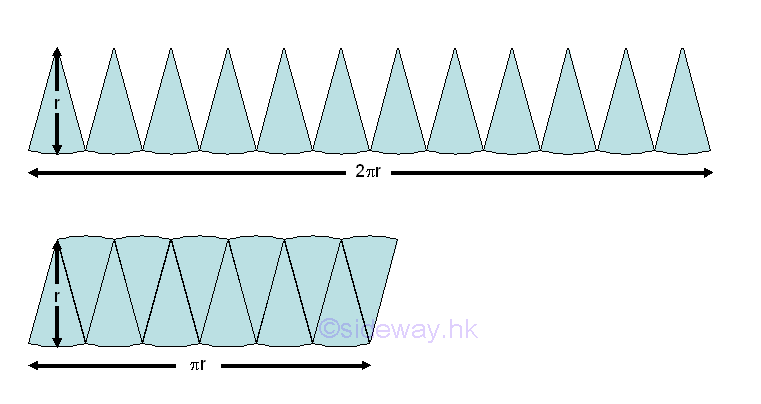
The area of a circle can also be determined by making use of pi in a similar way. Constant pi, π is the ratio of the circumference C to diameter d for a circle. The circumference of a circle can be considered as the instantaneous change of the area of a circle over a infinitely small change in radius at a specific position along the raduis. Imply
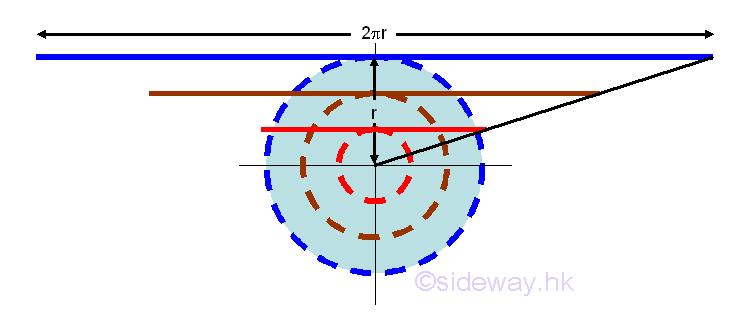
Mathematically, the relationship between area and circumference can be expressed as,
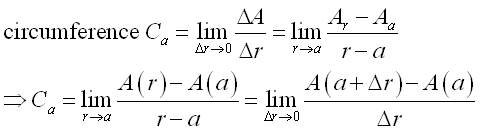
Therefore, the instantaneous effect of the circumference over an infinitely small radius interval Δr at a specific position a of the radius is the instantaneous area of the circle at a. Imply
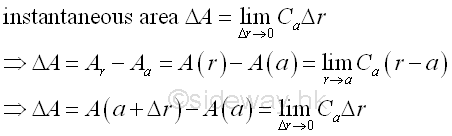
And the area of a circle is therefore equal to the summation of all area of infinitely small circumference strip over the region from radius 0 to r. Since the ratio of circumference to diameter is a constant, all the infinitely small circumference strips can form a triangle as the number of infinitely narrow circumference strips increases to infinity. Imply the area of circle is
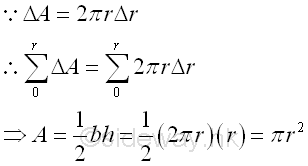
Derivatives and integrals
Calculus has two major branches of operation, derivatives and integrals.
Where the derivative of a function f(x) is the instantaneous rate of change of the function f(x) when x approaching a.
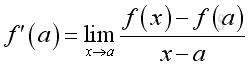
And the integral of a function g(u) is equal to the sum of individual signed area bounded by the function g(u) within the interval [x,a], that when x approaching a
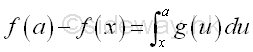
Although the derivative and integral operations are two different methods of operation, the basic concept of applying limits are the same. For a continuous function f on [a,b], when a approaching x
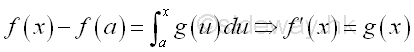
©sideway
ID: 110900001 Last Updated: 1/31/2013 Revision: 2 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
