Content
Kinetics: Work and Energy
Work of a Force
Work of a Constant Applied Force
in Rectilinear Motion
Work of a
Variable Applied Force
in Rectilinear Motion
Work Done by a Compressed Spring
Work of a Variable Applied Force in
Curvilinear Motion
Work of a Gravitational Force
Work of a Constant Applied Force in
Curvilinear Motion
Work of Force of Gravity
Kinetics: Work and Energy
Besides the dynamic equilibrium approach of the motion of an object as used in static equilibrium, the motion of an object can also be studied kinetically. One common kinetic approach is the method of work and energy.
Work of a Force
By Newton's First Law, force is always needed to be applied upon an object in order to change the motion of the object. For the kinetic motion of the object, a concept of work or work done is defined to quantify the kinetic motion of an object which is expressed as the product of the applied force acted upon the object and the displacement of the object due to the applied force. In other words, work is done by a force mechanically when there is a displacement at the point of application in the line of action of the force with magnitude equal to the product of the applied force and the linear displace along the line of action of the force.
By definition, the scalar product of two vectors is a scalar quantity of no direction with magnitude and sign only. Since the angle between the force vector and the displacement is from 0≤θ≤180o , the value of work done is negative when the angle is 90o<θ≤180o . And if the force vector is perpendicular to the displacement, i.e angle=90o , then no work is done. Therefore the positive sense of work done with the direction of displacement along with the direction of force is the work done by the force on the object, while the negative sense may be considered as the work done by the object with the reaction force of same magnitude and opposite sense to react the applied force.
In general, work done by a force is dependent on the path C travelled. But for a conservative force, the total work done by a conservative force only depends on the displacement and is independent on the path C travelled. And for a non-conservative force, like friction, the total work done is dependent on the path travelled.
Work of a Constant Applied Force in Rectilinear Motion
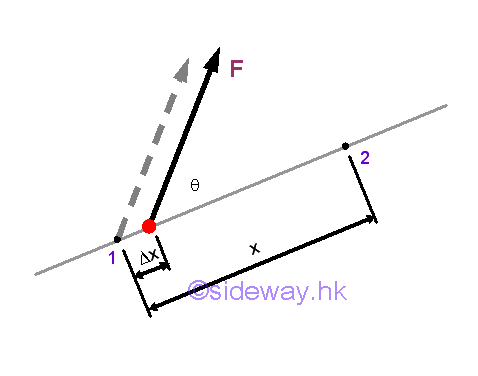
A displacement is the change of the position. When an object is in rectilinear motion, the object moves in a straight line. The displacement of a body is equal to the linear displacement of the body. By definition, the work done by the applied force on the object is equal to the product of the constant magnitude of the force along the displacement times and the displacement from point 1 to point 2.
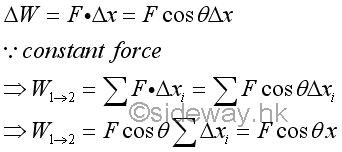
Work of a Variable Applied Force in Rectilinear Motion
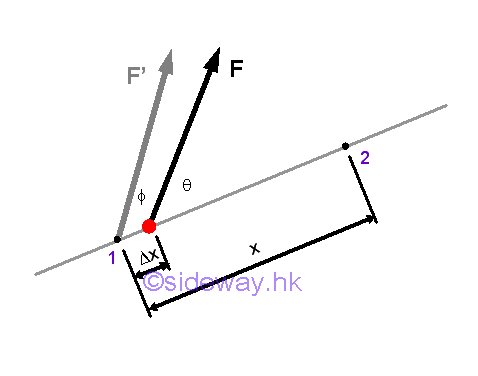
When the applied force varies with the distance travelled, the work done by the variable force in rectilinear motion can not be obtained by the direct multiplication of force by displacement. Instead, calculus is needed to find the work done by the force through the distance travelled by the object on which it acts.
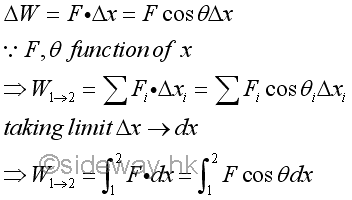
Work Done by a Compressed Spring
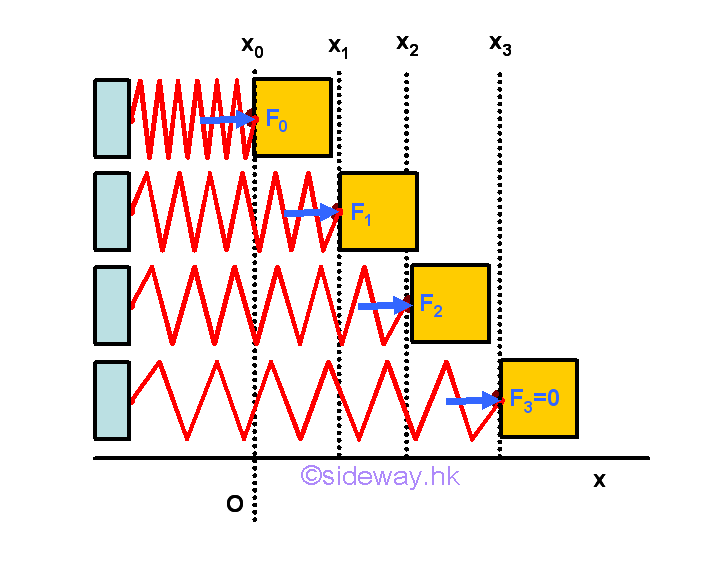
From experimental result, the magnitude of the force F exerted by a spring is proportional to the deflection x of the spring, that is F=kx, where k is the spring constant. For a compressed spring with preload force Fo, the force exerted by the compressed spring to the object decreases as the length of compressed spring extends and the reduced force is proportional to the extension of the spring.
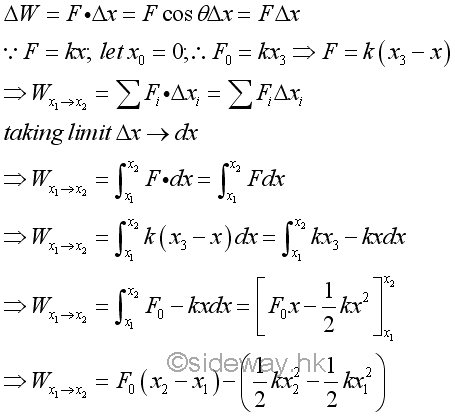
Work done by a preload spring is positive because both force and displacement are in the same direction. Graphically, the force exerted by the spring can be represented by a stright line and the work done by the preload spring is therefore equal to the area of the trapezoid under the curve throught the displacement of the spring.
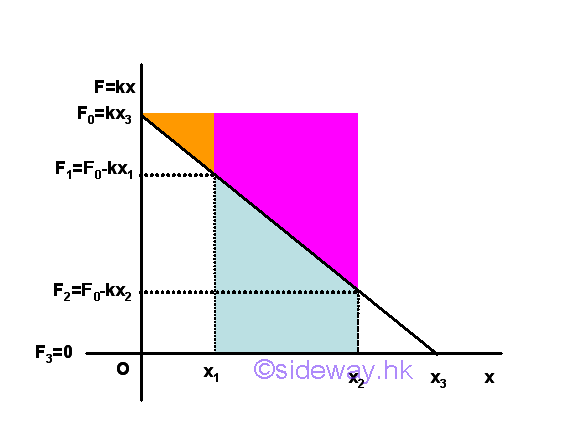
When the spring returns to the undeformed position, the force exerted by the spring is equal to zero. When the spring is further extended, the force exerted by the spring becomes negative in sense which means that the exerted force is opposite to the displacement in sense and the spring is in extension. Besides, the trapezoid area under the curve through the displacement can also be obtained by the mean force exerted by the spring.
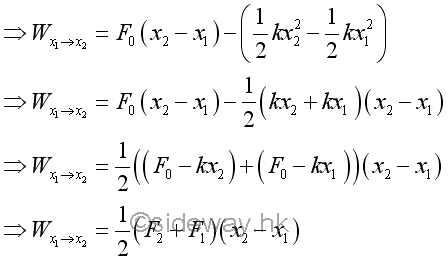
Work of a Variable Applied Force in Curvilinear Motion
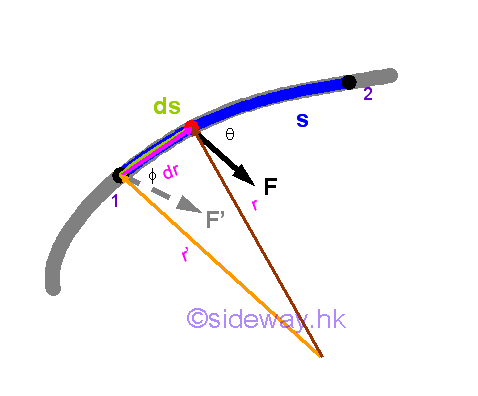
Similar to a variable applied force in rectilinear, when the applied force varies with the distance travelled, the work done by the variable force in curvilinear motion can not be obtained by the direct multiplication of force by displacement. Instead, calculus is needed to find the work done by the force through the distance travelled by the object on which it acts. Although a finite travelled distance is not a vector quantity, the infinitesimal travelled distance can be approximated by an infinitesimal displacement vector quantity also. Therefore an infinitesimal work done by a force acting on a body with an differential displacement can be expressed as the scalar product of the force vector and the displacement vector. Imply
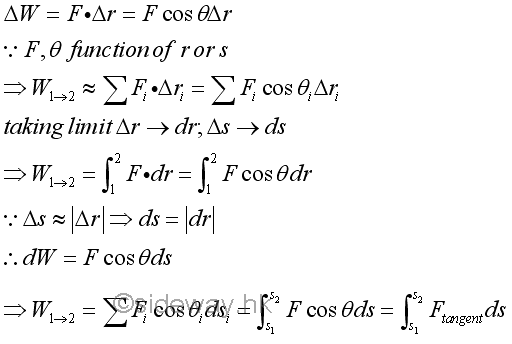
Similarly, the work done by an applied force can also be expressed in rectangular coordinates.
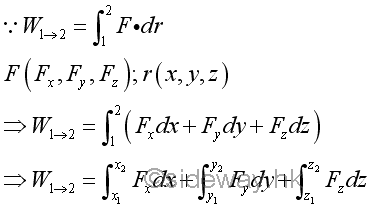
Work of a Gravitational Force
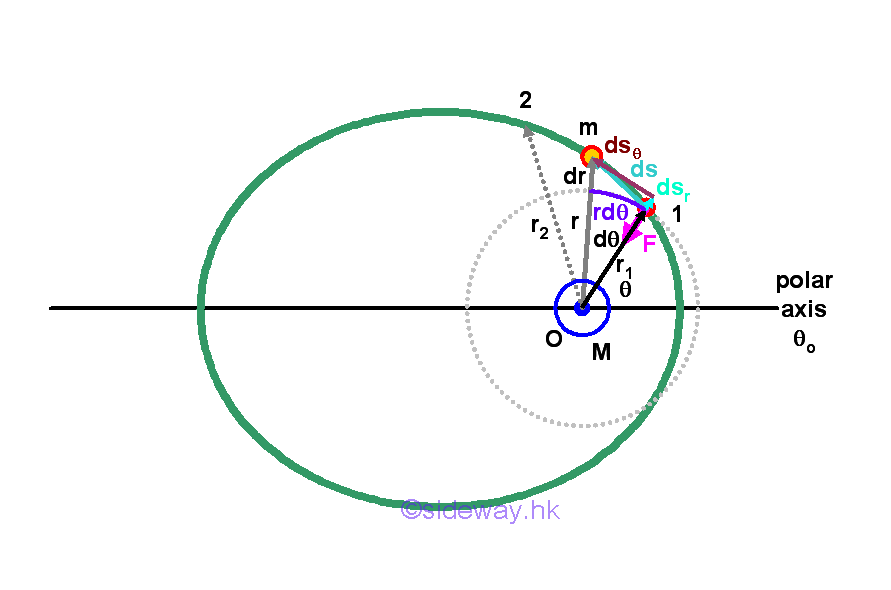
When expressing the planetary motion in polar coordinates, the gravitational force reduces to a radial component only. Therefore, the work done by the radial gravitational force acts on an object can also be obtained accordingly.

The negative sense of the gravitational force indicates that the gravitational force acts on the object is always directed toward the centre O. The work done by the gravitational force is negative, when the radial distance is increasing and the object is away from the centre O. While the work done by the gravitational force is positive, when the radial distance is decreasing and the object is away from the centre O.
Work of a Constant Applied Force in Curvilinear Motion
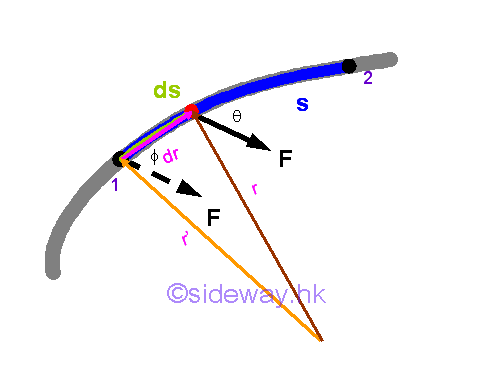
When an applied force is constant, both the magnitude and direction of the applied force is constant. However the angle between the force vector and the displacement vector is not a constant. Imply
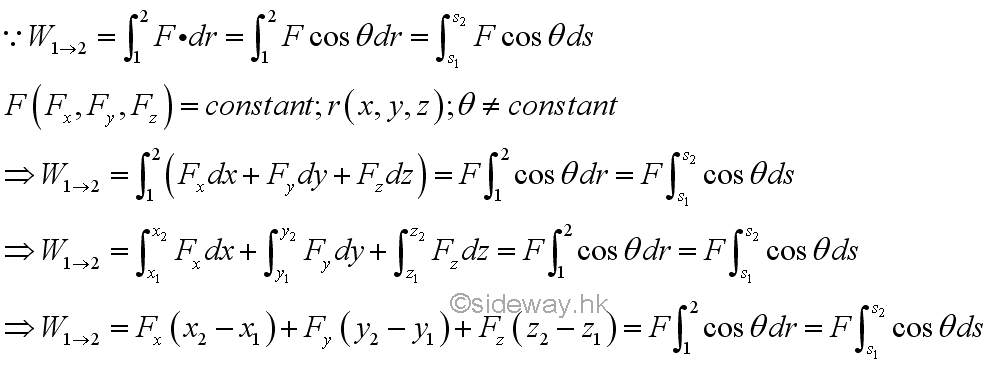
Work of Force of Gravity
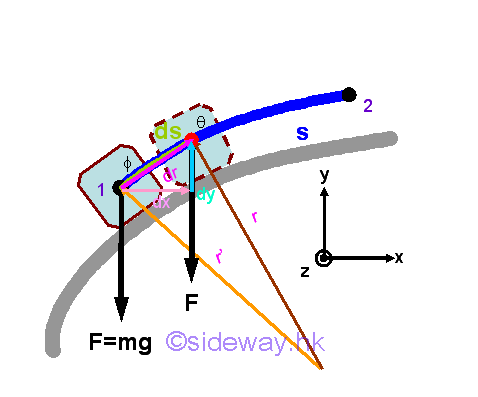
The force of gravity acts upon an object on earth surface is assumed to be constant when the displacement of the object is small. Since the weight of an object due to the force of gravity consists of only one rectangular component along the vertical direction, the work done by the force of gravity is equal to the weight of the object time the vertical displacement of the object. Imply
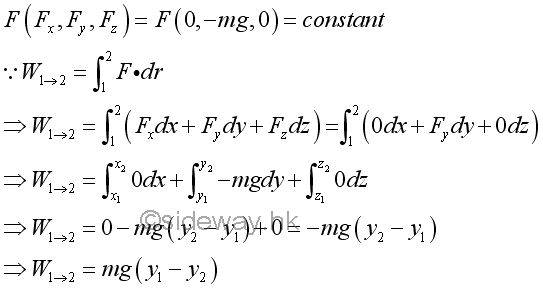
By neglecting the friction and considering the weight of the object only, the work done by the force of gravity on the object moving from position 1 up to position 2 is negative because the direction of the force of gravity is opposite to the direction of displacement. Since only the force of gravity is considered, the force acting upon the the object is a conservative force. Therefore, the work done due to the force of gravity acts on the object to move from position 1 to position 2 will be of the same magnitude but negative in sense to indicate that the direction of the displacement is of opposite sense with respect to the direction of the force. In other words, a work done by an applied force is required to move the object from position 1 to position 2 and the applied force is of the same magnitude but opposite in sense to the force of gravity. However, no applied force is needed to move the object from position 2 down to position 1 because the force of gravity will cause the object to slide down freely.
©sideway
ID: 141100001 Last Updated: 11/18/2014 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Rampage II Extreme(last updated On 8/23/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/16/2023)
- MagicPro ProHDTV(last updated On 7/15/2023)
- ROG STRIX Z690-A GAMING WIFI D4 CPU, BIOS, Chipset(last updated On 7/15/2023)
- Intel Core Processor(last updated On 7/14/2023)
- AVerMedia Live Gamer HD 2 - GC570(last updated On 7/13/2023)
- R2E Document(last updated On 7/11/2023)
- R2E Driver and Utility(last updated On 7/10/2023)
- R2E CPU, BIOS, Chipset(last updated On 7/9/2023)
- ASRock X58 Deluxe(last updated On 7/8/2023)
- ASRock X58 Deluxe(last updated On 7/7/2023)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Reference 79
Computer
Hardware 249
Software
Application 213
Digitization 32
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 429
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
