Sound Transmission in two mediums

In medium 1, when an ongoing harmonic wave strikes normally on the interface surface of medium 1 and medium, part of the incident sound energy is reflected back into the medium 1 and part of the incident sound energy is transmitted into the medium 2. 

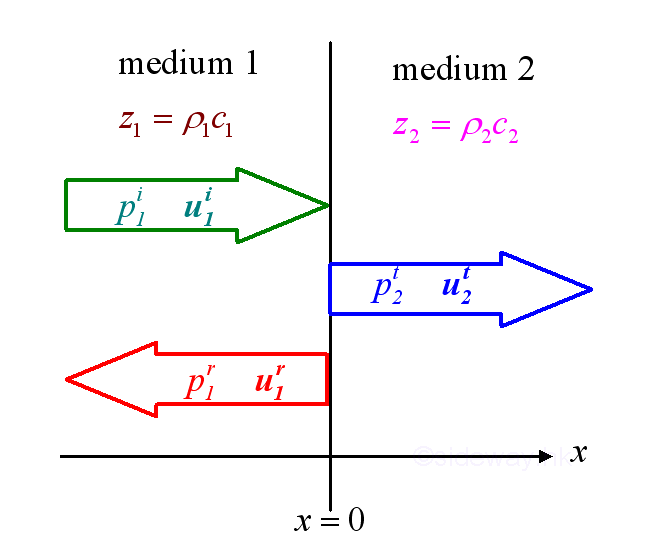
The impedances of the mediums are:

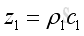and

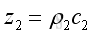
The frequencies of three waves must be the same. For two different mediums, the speed of wave propagation will be different for the two medium, therefore the corresponding wave numbers are:

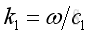and

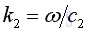
Assuming the three waves are harmonic plane waves in complex form imply

The normal incident wave:

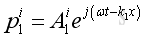
The reflected wave due to the hitting of normal incident wave on the medium interface at x=0:

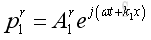
The transmitted wave inside the medium 2 caused by the normal incident wave:

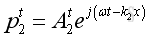
Therefore the total acoustic pressure due to the incident wave and reflected wave in medium 1 can be expressed as

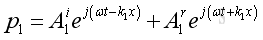
And the total acoustic pressure due to the transmitted wave in medium 2 can be expressed as

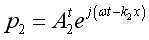
At the boundary, x =0 the waves of propagation are in equilibrium, therefore for all time, these waves must satisfies the boundary condition at all point on the boundary.

Let

p₁ be the total acoustic pressure at x=0 in medium 1
p₂ be the total acoustic pressure at x=0 in medium 2
u₁ be the net particle velocity at x=0 in medium 1
u₂ be the net particle velocity at x=0 in medium 2

Therefore, these waves should satisfy the two continuity conditions at the interface:

1. The total acoustic pressure in medium 1 at x=0 must equals to the total acoustic pressure in medium 2 at x=0, that is pressure continuity, imply
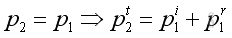
2. The net particle velocity in medium 1 at x=0 must equals to the net particle velocity in medium 2 at x=0, that is velocity continuity, imply

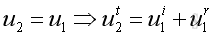
The particle velocities can be expressed in term of acoustic pressure, and get

for incident wave along +x direction:

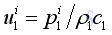
for reflected wave along -x direction:

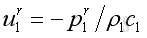
for transmitted wave along +x direction:

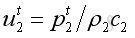
Therefore the velocity continuity equation can be expressed in term of acoustic pressure as 

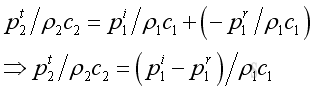
Imply pressure continuity at x=0:

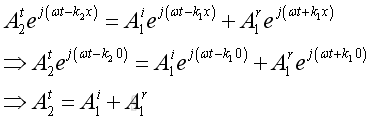
Imply velocity continuity at x =0:

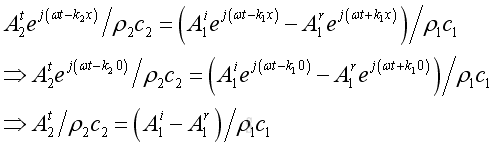
Pressure Reflection Coefficient

Eliminating the amplitude of transmitted  wave by substitute the pressure continuity into the velocity continuity, get:

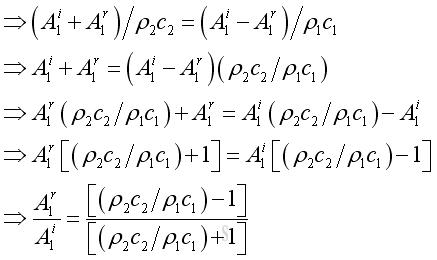
By definition, the presssure ratio of the reflected wave over the incident wave is the pressure reflection coefficient, imply:

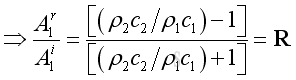
Pressure Transmission Coefficient

Eliminating the amplitude of reflected  wave by adding the pressure continuity to the velocity continuity, get:

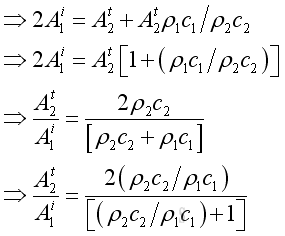
By definition, the pressure ratio of the transmitted wave over the incident wave is the pressure transmission coefficient, imply:

From the pressure continuity, the transmitted coefficient can be expressed as:

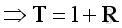
Intensity

At the medium interface, the intensity should be in equilibrium, imply

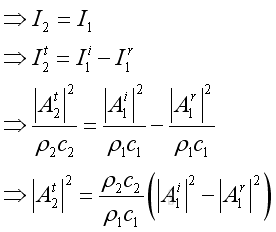
Therefore, the relationship between the reflection coefficient and transmission coefficient. imply

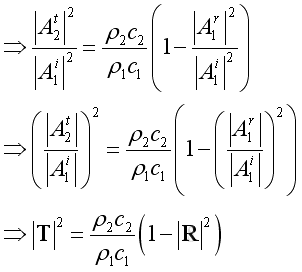
Intensity Reflection Coefficient

By definition, the intensity reflection coefficient or the reflection coefficient is the ratio of reflected acoustic power over incident acoustic power

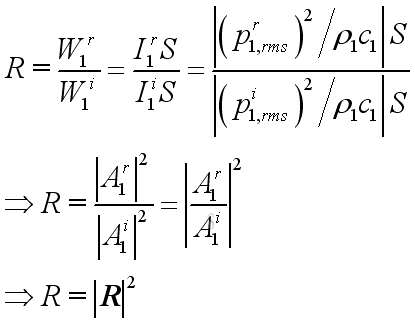
or

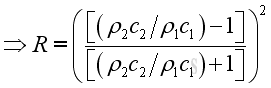
Intensity transmission Coefficient

By definition, the intensity transmission coefficient or the transmission coefficient is the ratio of transmitted acoustic power over incident acoustic power

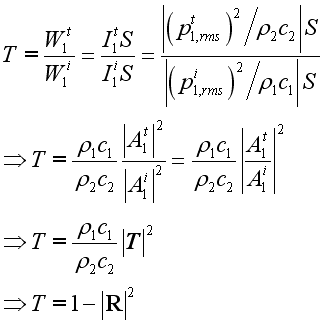
or

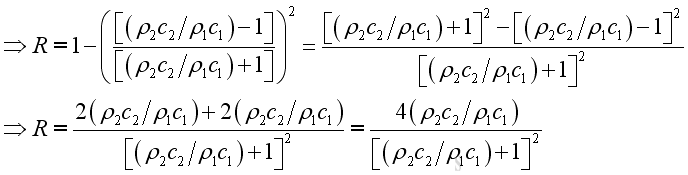
Absorption Coefficient

By definition, the sound power absorption coefficient is defined as the ratio of acoustic power entering the medium interface over the sound power of incident wave

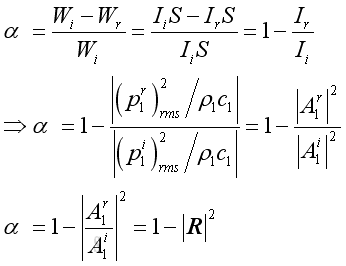
Impedance

When z₁=z₂, ratio=1 imply R = 0, T=1, imply total transmission

When z₁<<z₂, ratio=infinity. imply R = 1, T=2, imply total reflection with same amplitude and phase. The transmitted wave has a pressure amplitude twice the amplitude of incident wave. The normal particle velocity at the medium interface is zero and is so called rigid medium.

When z₁>>z₂, ratio=0, imply R = -1, T=0, imply total transmission. The reflected wave is the same amplitude with the incident wave but 180degree out of phase. The transmitted wave therefore has zero pressure amplitude. The acoustic pressure at he medium interface is zero and is so called pressure release.

Therefore impedance match is important on acoustic control.

For example:

Air to water: z₁= 400; z₂ = 1450000 kg/m.s, imply a=3625, R=0.9995,T=2; absorption=0.001. Only a small quantity of energy transmitted.

Water to Air : z₁= 1450000; z₂ = 400 kg/m.s, imply a=2.75x10-4, R=-0.9995,T=0; absorption=0.001. In practice nearly no energy gets through,