Content
Infinitely Many
Prime Numbers
Washington's
Proof (1980)[1]
Furstenberg's
Proof (1955)[1]
Euclidean Sequences [1]
Pairwise Relatively Prime Sequences [1]
Infinitely Many Prime Numbers
"There exist infinitely many prime numbers" as there are infinitely natural numbers on the number line. Many supporting proofs can support the existence of infinitely prime numbers along the number line.
Washington's Proof (1980)[1]
Washington's method is via commutative algebra. Consider the field of all numbers with the form a+b√(-5) where a, b are rational numbers. Therefore the ring of algebraic integers in this field are numbers of the same form with a, b can only be ordinary integers only. In this ring, 2, 3, 1+√(-5), 1-√(-5) are prime elements bescause these numbers have no other algebraic integer prime factor besides the "unit" 1 or -1. 6 is a composite element in the ring of algebraic integers. And the number 6 can be decomposited into 2x 3 or (1+√(-5))(1-√(-5)). The product of primes of number 6 is not unique up to units, so this ring is not a unique factorization domain. Since the ring of algebraic integers in every number field of finite degree is a Dedekind domain, where every nonideal is the product of prime ideals in a unique way. And for a Dedekind domain with only finitely many prime ideals is a principal ideal domain, where every nonelement is the product of prime elements in a unique way and is up to units. Therefore this ring is not a principal ideal domain and there must have infinitely many prime ideals. And in every number field of finite degree, there are only finitely many prime ideals that divide any given prime number. The infinitely many prime ideals imply there exist infinitely many prime numbers.

Furstenberg's Proof (1955)[1]
Furstenberg's Method is based on ideas of topology. Considering the
set of integers Z={..., -3. -2, -1, 0, 1, 2, 3, ...}, let collection B of
subsets of Z be the evenly topological space of integer from -∞ to +∞ of using
arithmetic progressions, as a basis for a topology on Z such that every element
of Z is contained in at least one basic element. The family of sets
B(a,b)={an+b|n∈Z}=aZ+b with a and b are whole number and a not equal to 0, is
the set of integers Z. Let x∈Bi, if Bi⊂Z, then x∈Bi⊂Z. Therefore if x∈B1∩B2
for any two basis elements Bi, there exists a basis
element B3 such that x∈B3⊂B1∩B2. A
topology on the set Z with the collection B of subsets of Z have properties that
∅ and Z are in the collection B. The union set of the basis elements of any
finite subcollection of collection B is also in B and the intersection set of the basis
elements of any finite subcollection of B is also in B. Therefore, Z is a topological
space with collection B. Consider a subset S of Z, set S is an open set of Z if S belongs to the
collection B. In order words, the topological space is the set Z with a collection of
subsets S of Z. These subsets S of Z are called open sets because one subset S
belongs to the collection of all subsets S, for example ∅ and X are
both open and the union of arbitrary open sets and the intersection of finite open
sets are open also. Similarly to the topology of Z generated by collection B, a
subset S of Z is said to be an open set in Z, if for each x∈S, there is a
basis element Bi∈B such that x∈Bi and Bi⊂S.
Since a set
S is called closed if its complement is open. Therefore S is both closed and
open because its complement is the union of other subsets S. And imply the union
of any finite number of subsets S is closed. Therefore the topological space on
Z have properties that
∅ and Z are closed because they are the complements of the open sets Z and ∅.
The arbitary intersection set of the closed sets are closed and the finite unions
of closed sets are closed. Since
family of sets B(a,b) are basis sets and are equal to the compliement of the union
of other basis sets, that is B(a,b)=Z\∪a-1
i=1
B(a,b+j), imply family of sets B(a,b) are closed. Therefore family of sets
B(a,b) are both open and closed. And also imply that the union of any finite
number of sets B(a,b) is closed. Besides set B(a,b)=aZ+b is infinite, every non
empty open set in the topology on Z is infinite, imply no finite set is open.
Consider one kind of subset A in the set Z, let set Ap
be all multiples of prime p, imply Ap=B(p,0)=pZ and set A is
equal to the union of all set Ap where p runs throught the set of primes ≥2,
i.e A=∪
p=primeAp. Since A consists all x in set Z except
-1 and 1, there exist another set {-1,1} and is the complement of A. That is A=∪
p=primeAp=Z\{-1,1}. The set
{-1,1} is finite and is not an open set, imply A cannot be closed. If there
exists only finitely many primes, a finite union of closed sets is equal to a
closed set which contradicts to the complement of a closed set. Since A is open,
A cannot be a finite union of closed sets and can only be an union of infinitely sets imply
there are infinitely many prime numbers.

Euclidean Sequences [1]
Similar to the Euclid's method, equation can be constructed to generate an infinite prime number sequence. Some typical sequences are:
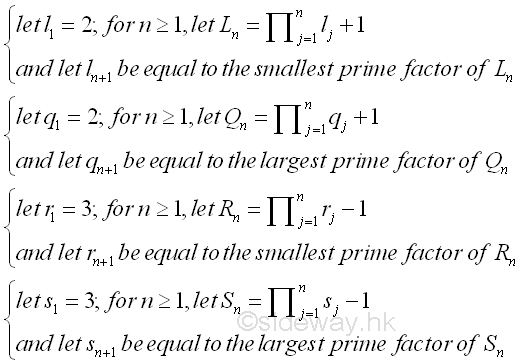
These sequences are not monotonic. These sequences do not contain all the primes and have been conjectured that infinitely many primes are excluded. For example, sequence of Ln is generated as
| 2*smallest+1 | 2*largest+1 | 3*smallest;-1 | 3*largest;-1 | |||||
|---|---|---|---|---|---|---|---|---|
| n | ln | Ln | qn | Qn | rn | Rn | sn | Sn |
| 1 | 2 | 2+1 | 2 | 2+1 | 3 | 3-1 | 3 | 3-1 |
| 2 | 3 | 2*3+1 | 3 | 2*3+1 | 2 | 3*2-1 | 2 | 3*2-1 |
| 3 | 7 | 2*3*7+1 | 7 | 2*3*7+1 | 5 | 3*2*5-1 | 5 | 3*2*5-1 |
| 4 | 43 | 2*3*7*43+1 | 43 | 2*3*7*43+1 | 29 | 3*2*5*29-1 | 29 | 3*2*5*29-1 |
| 5 | 13*139 | 2*3*7*43*13+1 | 13*139 | 2*3*7*43*139+1 | 11*79 | 3*2*5*29*11-1 | 11*79 | 3*2*5*29*79-1 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... |
An infinite prime number sequence can also be generated from the sequence of known existing primes. Let pn be the nth of prime number, the product of the first n primes is called the primorial pn#. The two sequences are pn#+1 and pn#-1. Imply
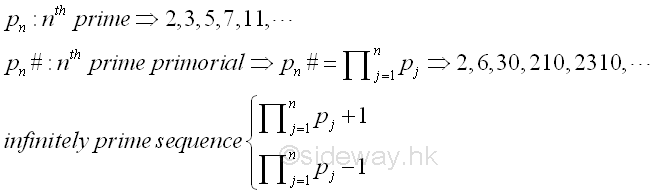
Similary, there are infinitely many generated prime only or composite are still unknown.
| n | pn | pn#+1 | pn#-1 | ||
|---|---|---|---|---|---|
| 1 | 2 | 2+1 | 3 | 2-1 | 1 |
| 2 | 3 | 2*3+1 | 7 | 2*3-1 | 5 |
| 3 | 5 | 2*3*5+1 | 31 | 2*3*5-1 | 29 |
| 4 | 7 | 2*3*5*7+1 | 211 | 2*3*5*7-1 | 11*19 |
| 5 | 11 | 2*3*5*7*11+1 | 2311 | 2*3*5*7*11-1 | 2309 |
| 6 | 13 | 2*3*5*7*11*13+1 | 59*509 | 2*3*5*7*11*13-1 | 30029 |
| ... | ... | ... | ... | ... | |
Pairwise Relatively Prime Sequences [1]
Similar to Goldbach's method of using an infinitely Pairwise Relatively Prime Sequences, Bellman (1947) proposed an induction method to generate infinite sequences of pairwise relatively prime integers. By method of induction, consider a polynomial f(x) with integral coefficients. then let f1(x)=f(x) and define fn+1(x)=f(fn(x)) for n≥1. For f(0)≠0 and n≥2, if f1(0)=f(0) and gcd(m,f(0))=1 such that m and f(0) are relatively prime integers, imply f(m) and f(0) are also relatively prime integers gcd(f(m),f(0))=1. Therefore by induction, let f1(x)=f(x) and for n≥1, let fn+1(x)=f( fn(x)). If fn(0)=f(0) and gcd(m,f(0))=1 then integers m, f1(m), f2(m), f3(m), ..., fi(m), fn(m), ... are pairwise relatively primes.

There are many particular cases of this theorem. For example, the Fermat number, Fn=22n+1 can be expressed as a polynomial f(x) with integral coefficients, f(x)=(x-1)2+1 with x equal to -1. Imply

Another example is from Edwards (1964) (or Mohanty, 1978), Edwards proposed a sequence generated by a recursive polynomial formula. Let a, S0 be non zero relatively prime integers; for n≥1, Sn is equal to Sn-1(Sn-1-a)+a. Similarly, S0, S1, S2, S3, ..., Sn, ... are pairwise relatively prime integers. One particular case is when a=2, S0=3, the sequences are S0=3, S1=5, S2=17, S3=257, ..., Sn, ... These sequences are same as the Fermat number sequence where Sn=Fn. In fact, these sequences can alse be obtained using the Bellman's method. Let function fn(x) be Sn. The Edwards's polynomial, Sn=Sn-1(Sn-1-a)+a is same as the Bellman's polynomial fn+1(x)=(fn(x))2-a(fn(x))+a. implies

Consider another infinite pairwise relatively prime sequences. Let w1=2, w2=w1+1=3,
w3=w1w2+1=7,wn+1=∏n
i=1wi. The
numbers w1, w2,
w3, ..., wn, ... are
pairwise relatively prime. When a prime pi dividing wi,
prime pi is distinct. Therefore primes p1, p2,
p3, ..., pn, ... are
all distinct primes. Similarly, the infinite pairwise relatively prime sequences
can be expressed as the Bellman's polynomial
fn+1(x)=(fn(x))2-(fn(x))+1. Implies
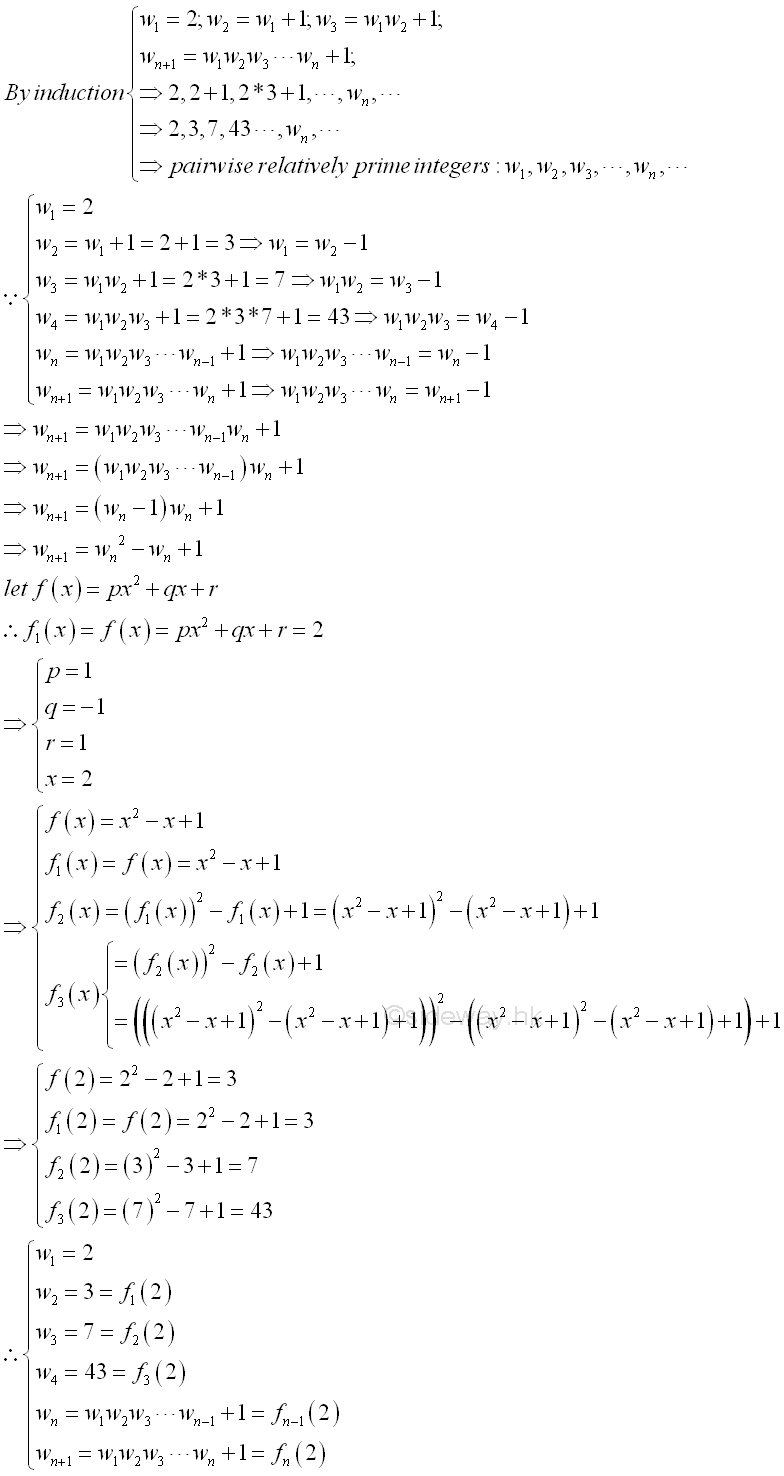
©sideway
ID: 130400009 Last Updated: 4/16/2013 Revision: 0 Ref:
References
- R. Paulo, 1996, The New Book of Prime Number Records
- Wolstenholme, R.J., 1862, On Certain Properties of Prime Numbers
- Mann, H.B., Shanks D., 1972, A Necessary and Sufficient Condition for Primality, and Its Source
- J.M Pollard, Kangaroos, 1975, A Monte Carlo Method for Factorization
Latest Updated Links
- Panasonic SR-CK05 RiceCooker CW-HZ70AA(last updated On 11/17/2025)
- Panasonic Hood Structure Ventilating Fan Blade Diameter: 8in FV-20WH307 CW-HZ70AA(last updated On 11/16/2025)
- Panasonic Window Mount Thermo Ventilator FV-30BW2H CW-HZ70AA(last updated On 11/15/2025)
- Panasonic Inverter PRO Inverter Window Heatpump Air-Conditioner (3/4 HP) CW-HZ70AA(last updated On 11/14/2025)
- Panasonic Inverter Window-Split Type Cooling Only Air-Conditioner (1 HP) CS-U9YWA(last updated On 11/13/2025)
- Panasonic Inverter Steam and Grill_Microwave Oven 27L NN_DS59NB(last updated On 11/12/2025)
- Panasonic KY-C223B Induction Cooker(last updated On 11/11/2025)
- Focus M41 Single lever kitchen mixer 160(last updated On 11/10/2025)
- Focus Single lever basin mixer 230(last updated On 11/9/2025)
- Precision Start Thermostat shower mixer(last updated On 11/8/2025)
- Tempesta 100 Shower Rail Set 3 sprays(last updated On 11/7/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 40
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
