Content
MatLab: Scratch Pad &
Arithmetic
Operations
Arithmetic
Operators
Matrix
Arithmetic Operations
+ Addition
Examples
+ Unary Plus
Examples
- Subtraction
Examples
- Unary Minus
Examples
* Matrix Multiplication
Examples
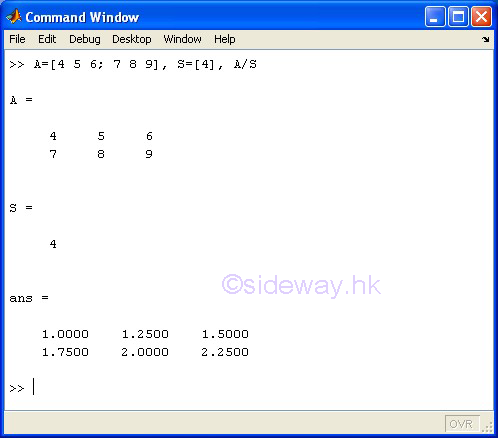
/ Slash or Matrix Right Division
Examples
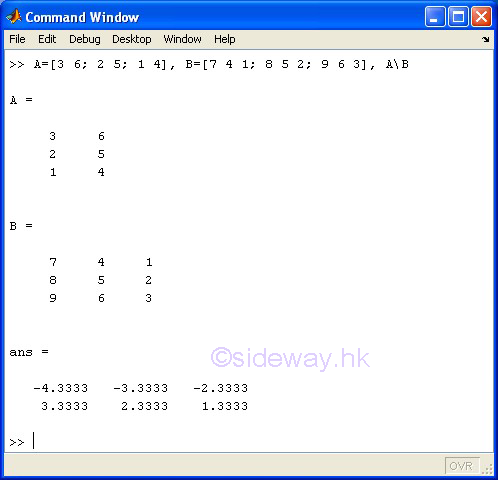
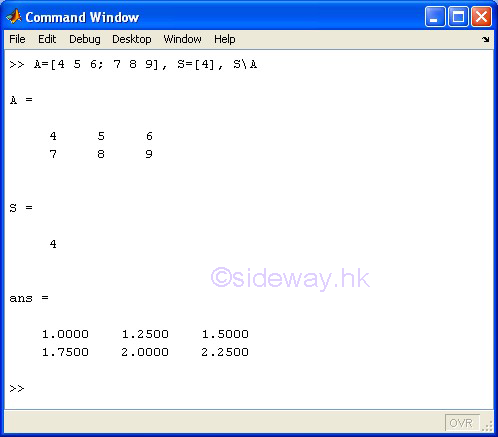
\ Backslash or Matrix Left Division
Examples
^ Matrix Power
Examples
'
Matrix
Transpose or Complex Conjugate Transpose
Examples
Array
Arithmetic Operations
+ Addition
Examples
+ Unary Plus
Examples
- Subtraction
Examples
- Unary Minus
Examples
.* Array Multiplication
Examples
./ Array Right Division
Examples
.\ Array Left Division
Examples
.^ Array Power
Examples
.'
Array Transpose
Examples
Arithmetic Operation Functions
Arithmetic Expressions
Operator Precedence
MatLab: Scratch Pad & Arithmetic Operations
Major Reference Source: MatLab Verson 7.0
Using MatLab package as a scratch pad interactively is one of the common application of the MatLab package. MatLab commands are entered at the prompt command, >>, of the Command Window through the PC keyboard. Both entered commands and evaluation results are displayed in the Command Window. All new line or lines of commands or instructions after the prompt command will be passed to MatLab for evaluation after pressing the Enter key no matter the position of mouse cursor is at the end of line or lines or not.
Arithmetic Operators
Since all types of data in MatLab are stored in the form of arrays, MatLab provides two different kinds of arithmetic operations, i.e. array operations and matrix operations. MatLab array operations are just ordinary arithmetic operations that supports multidimenstional arrays for processing element by elemt operations. While MatLab matrix operation are ordinary matrix operations that following the rules of linear algebra. Both array operations and matrix operations share the similar symbols of operation, a period characater, "." is used to distinguish the array operations from the matrix operations. However, as the addition and subtraction for both matrix operation and array operation are the same, the period characater, "." is not necessary and the character pairs ".+" and ".-" are not used. Besides, the 1-by-1 array, scalar, is also a special type of MatLab array. A 1-by-1 array, scalar can have array operation with an array of any size also. A 1-by-1 matrix, scalar can also have martrix operation with a matrix of any size, but limited by the matrix multiplication, the 1-by-1 matrix, scalar can only be the divisor of the right and left division.
The matrix and array arithmetic includes seven types of operations:
|
Arithmetic Operators |
Matrix
Arithmetic Operations |
Element-Wise
Array
Arithmetic Operations |
||
|---|---|---|---|---|
| Syntax | Description | Syntax | Description | |
|
Addition + |
A+B | Addition | A+B | Addition |
| +A | Unary Plus | +A | Unary Plus | |
|
Subtraction - |
A-B | Subtraction | A-B | Subtraction |
| -A | Unary Minus | -A | Unary Minus | |
|
Multiplication * |
A*B |
Matrix
Multiplication |
A.*B |
Array
Multiplication |
|
Right Division / |
A/B | Forward Slash or Matrix Right Division | A./B |
Array
Right Division |
|
Left Division \ |
A\B | Backslash or Matrix Left Division | A.\B |
Array
Left Division |
|
Power ^ |
A^B | Matrix Power | A.^B | Array Power |
|
Transpose ' |
A' |
Matrix
Transpose or Complex Conjugate Transpose |
A.' | Array Transpose |
Matrix Arithmetic Operations
+ Addition
The + addition operator of the expression A+B means adds matrix B to matrix A. Since only a scalar can be added by or added to a matrix of any size, unless either A or B is a scalar, A and B must have the same size.
Examples
-
m-by-n matrix A + m-by-n matrix B
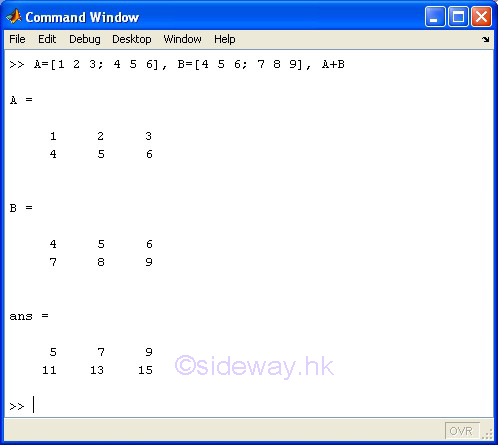
-
scalar S + matrix A + scalar S
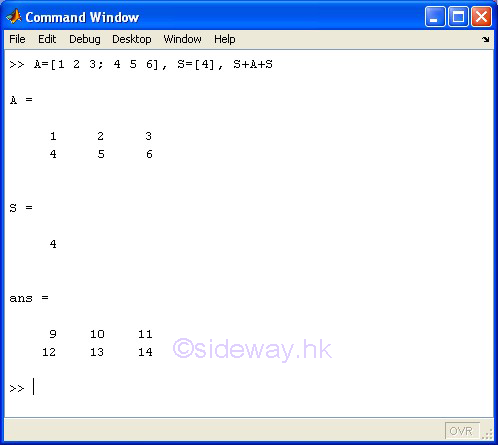
+ Unary Plus
The + unary plus operator of the expression +A means returns matrix A.
Examples
-
+matrix A

- Subtraction
The - subtraction operator of the expression A-B means subtracts matrix B from matrix A. Since only a scalar can be subtracted by or subtracted from a matrix of any size, unless either A or B is a scalar, A and B must have the same size.
Examples
-
m-by-n matrix A - m-by-n matrix B
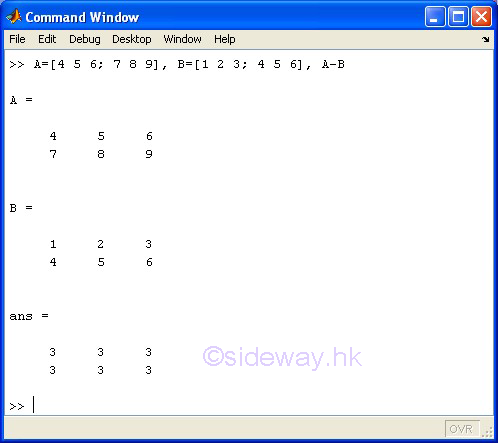
-
scalar S - m-by-n matrix A - scalar S
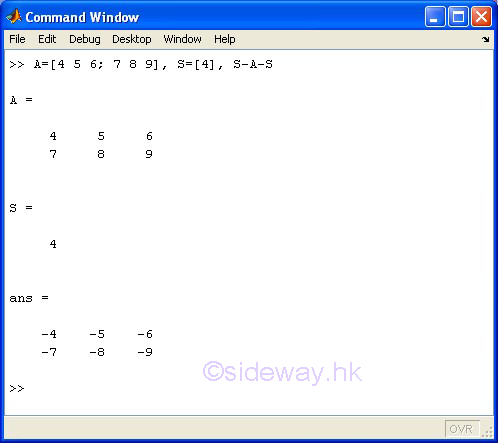
- Unary Minus
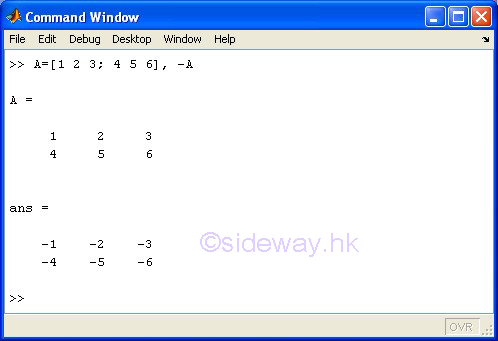
The - unary minus operator of the expression -A means returns and negates the elements of matrix A.
Examples
-
-matrix A
* Matrix Multiplication
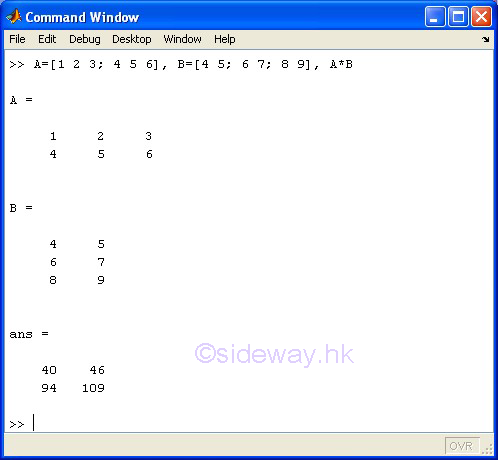
The * matrix multiplication operator of the expression A*B means to carry out the linear algebraic product of matrix A by matrix B.
Since only a scalar can be multiplicated by or multiplicated to a matrix of any size, two or more dimensions are supported, unless either A or B is a scalar, otherwise the number of columns of matrix A must equal to the number of rows of matrix B.
Examples
-
m-by-n matrix A * n-by-o matrix B
-
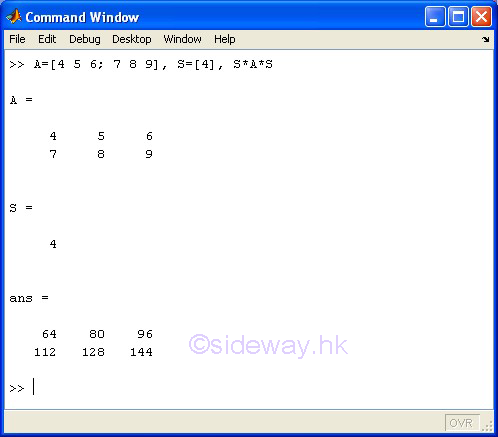
scalar S * m-by-n matrix A * scalar S
/ Slash or Matrix Right Division
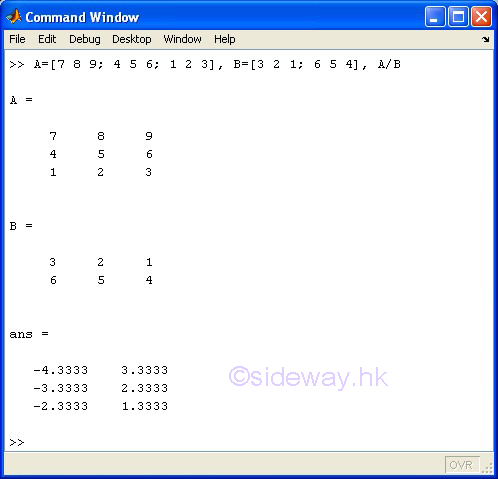
The / slash or matrix right division operator of the expression A/B means to carry out the linear algebraic product of matrix A by the inverse of matrix B, A*inv(B), in a general sense of the solution to the equation xB=A or A/B equals to (B'\A')'
Limited by the linear algebraic product of matrix, only a scalar can divide a matrix of any size, unless B is a scalar, otherwise both matrices A and B must have the same number of columns.
Examples
-
m-by-n matrix A / o-by-n matrix B
-
matrix A / scalar S
\ Backslash or Matrix Left Division
The \ backslash or matrix left division operator of the expression A\B means to carry out the linear algebraic product of the inverse of matrix A by matrix B, inv(A)*B, in a general sense of the solution to the equation Ax=B.
Limited by the linear algebraic product of matrix, only a scalar can divide a matrix of any size, unless A is a scalar, otherwise both matrices A and B must have the same number of rows.
Examples
-
m-by-n matrix A \ m-by-o matrix B
-
scalar S \ matrix A
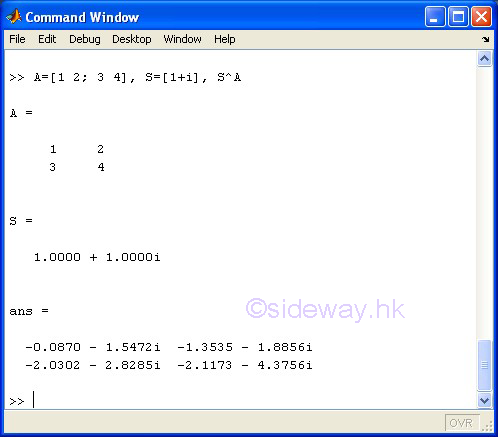
^ Matrix Power
The ^ matrix power operator of the expression A^B means to carry out the matrix A to the power of matrix B. However, one of the matrices A and B must be a scalar and the other matrix must be a square matrix.
If B is a scalar of a positive integer and A is a matrix, the matrix power means repeated matrix multiplication of matrix A by itself of the value of scalar B times. If B is scalar of a negative integer, the matrix power means repeated matrix multiplication of the inverse of matrix A by itself to the absolute value of scalar B times. If B is a scalar not equal to an integer and A is a matrix, the matrix power means the calculation involves eigenvalues and eigenvectors, such that if [V,D]=eig(A), then A^B=V*D.^B/V.
If A is a scalar and B is a matrix, the matrix power also means the calculation involves eigenvalues and eigenvectors, such that if [V,D]=eig(A), then A^B=V*D.^B/V.
Examples
-
square matrix A ^ scalar S of positive integer
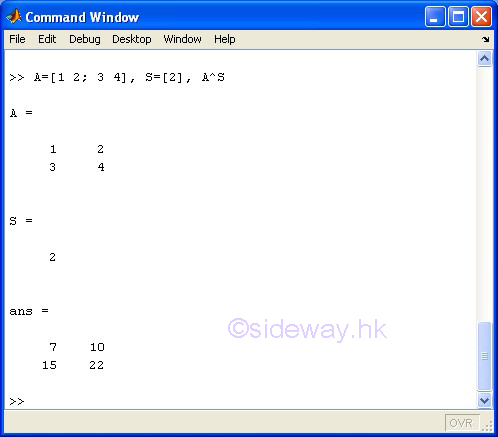
-
square matrix A ^ scalar S of negative integer
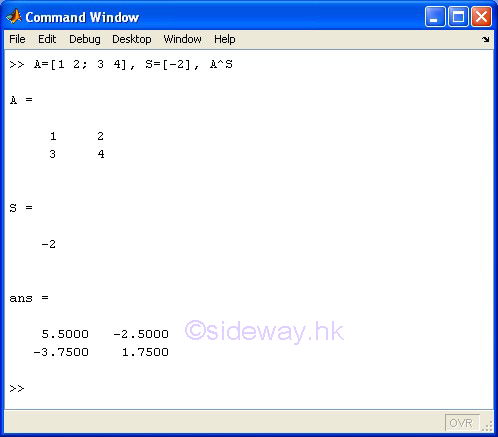
-
square matrix A ^ scalar S of non-integer
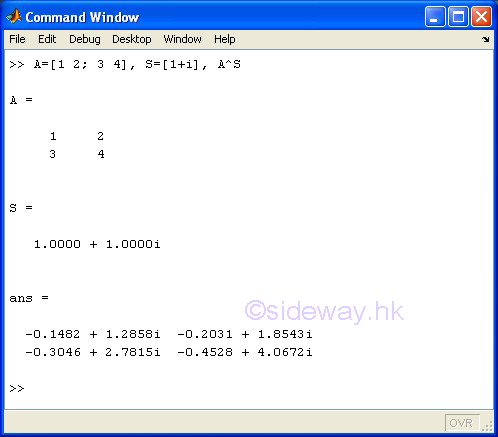
-
scalar S ^ square matrix A
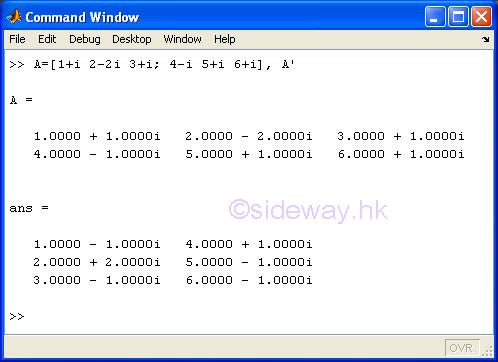
' Matrix Transpose or Complex Conjugate Transpose
The ' matrix transpose or complex conjugate transpose operator of the expression A' means to carry out the linear algebraic transpose of matrix A. If matrix A is a complex matrix, the matrix transpose operator means to carry out the complex conjugate transpose.
Examples
-
m-by-n matrix A'
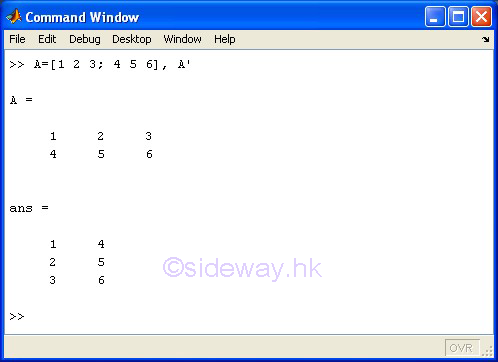
-
m-by-n complex matrix A'
Array Arithmetic Operations
+ Addition
The + addition operator of the expression A+B means adds B to A. Since only a scalar can be added to a matrix of any size, unless either A or B is a scalar, A and B must have the same size.
Examples
-
m-by-n-by-o array A + m-by-n-by-o array B

-
scalar S + m-by-n array A + scalar S

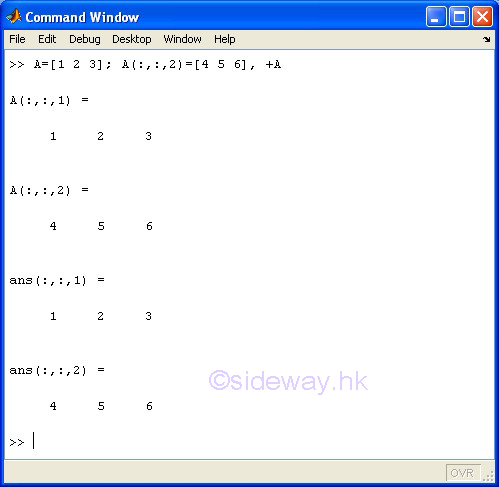
+ Unary Plus
The + unary plus operator of the expression +A means returns A.
Examples
-
+array A
- Subtraction
The - subtraction operator of the expression A-B means subtracts B from A. Since only a scalar can be subtracted by or subtracted from a matrix of any size, unless either A or B is a scalar, A and B must have the same size.
Examples
-
m-by-n-by-o array A - m-by-n-by-o array B

-
scalar S - m-by-n-by-o array A - scalar S

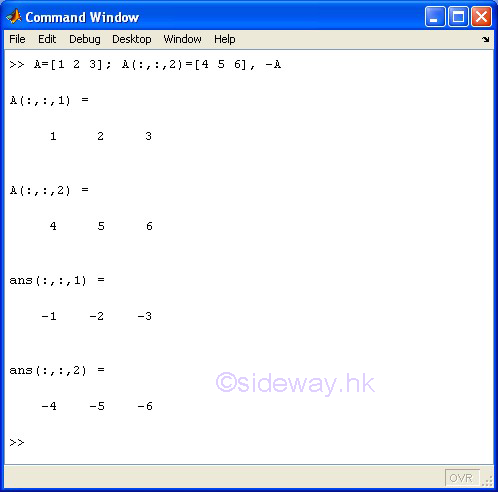
- Unary Minus
The - unary minus operator of the expression -A means returns and negates the elements of A.
Examples
-
-array A
.* Array Multiplication
The .* array multiplication operator of the expression A.*B means to carry out the element by element product of array A by array B.
Since only a scalar can be multiplicated by or multiplicated to a matrix of any size, unless either A or B is a scalar, otherwise the size of arrays A and B must be equal. Arrays with two or more dimensions are supported.
Examples
-
m-by-n-by-o array A .* m-by-n-by-o array B

-
scalar S .* m-by-n-by-o array A .* scalar S

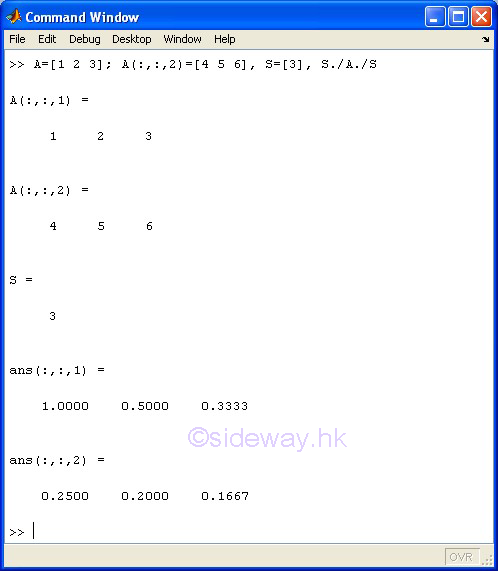
./ Array Right Division
The ./ array right division operator of the expression A./B means to carry out the element by element division of array A by array B.
Since only a scalar can be divided by or divide an array of any size, unless either A or B is a scalar, otherwise the size of arrays A and B must be equal. Arrays with two or more dimensions are supported.
Examples
-
m-by-n-by-o array A ./ m-by-n-by-o array B

-
scalar S ./ m-by-n-by-o array A ./ scalar S
.\ Array Left Division
The .\ array left division operator of the expression A.\B means to carry out the element by element division of array B by array A.
Since only a scalar can be divided by or divide an array of any size, unless either A or B is a scalar, otherwise the size of arrays A and B must be equal. Arrays with two or more dimensions are supported.
Examples
-
m-by-n-by-o array A .\ m-by-n-by-o array B

-
scalar S .\ m-by-n-by-o array A .\ scalar S

.^ Array Power
The .^ array power operator of the expression A.^B means to carry out the element by element calculation of the element of array A to the corresponding element of array B.
Since only a scalar can be carried out the element by element operation to an array of any size, unless either A or B is a scalar, otherwise the size of arrays A and B must be equal. Arrays with two or more dimensions are supported.
Examples
-
m-by-n-by-o array A .^ m-by-n-by-o array B

-
scalar S .^ m-by-n-by-o array A .^ scalar S

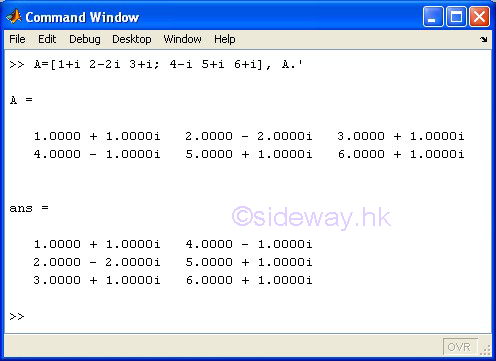
.' Array Transpose
The .' array transpose of the expression A.' means to carry out the two dimensional array transpose of array A for both real and complex array and no complex conjugation is involved. Only one or two dimensional arrays are supported
Examples
-
m-by-n array A.'

-
m-by-n complex array A.'
Arithmetic Operation Functions
The function of an arithmetic operator also have its corresponding function call.
| Operation | Description | Function Form |
|---|---|---|
| A+B | Binary Addition | plus(A, B) |
| +A | Unary Plus | uplus(A) |
| A-B | Binary Subtraction | minus(A, B) |
| -A | Unary Minus | uminus(A) |
| A*B |
Matrix
Multiplication |
mtimes(A, B) |
| A/B | Forward Slash or Matrix Right Division | mrdivide(A, B) |
| A\B | Backslash or Matrix Left Division | mldivide(A, B) |
| A^B | Matrix Power | mpower(A, B) |
| A' |
Matrix
Transpose or Complex Conjugate Transpose |
ctranspose(A) |
| A.*B |
Array
Multiplication |
times(A, B) |
| A./B |
Array
Right Division |
rdivide(A, B) |
| A.\B |
Array
Left Division |
ldivide(A, B) |
| A.^B | Array Power | power(A, B) |
| A.' | Array Transpose | transpose(A) |
Arithmetic Expressions
An arithmetic expression is an expression used to represents a numeric value. Arithmetic expressions are built up from numbers, arithmetic operators and parenthese, etc. following some predefined rules and operator precedence.
Operator Precedence
An expression is usually formed from a combination of arithmetic, relational, and logical operators. Arithmetic operators are the most common operators used for performing arithmetic calculation on numbers. MatLab always evaluates expressions from left to right, however the order of operators to be evaluated by MatLab within an expression are determined by the precedence levels of operators. The following operator with a higher precedence level will override the rule of from left to right evaluation. While the operator will be evaluated immediately if the following operator has the same or lower precedence level. The precedence rules for MatLab operators are
| Precedence Level | Operators |
|---|---|
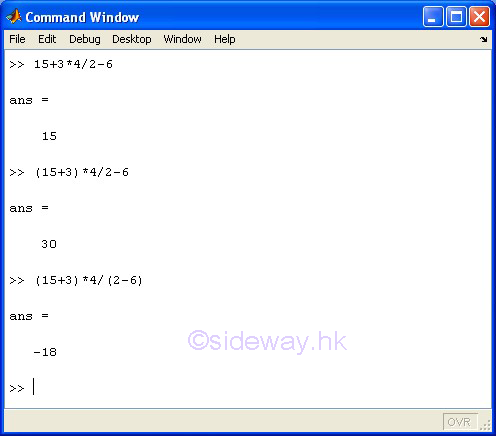
| 1 | Parentheses () |
| 2 | Transpose .' ; Power .^ ; Complex conjugate transpose ' ; Matrix power ^ |
| 3 | Unary plus + ; Unary minus - ; Logical negation ~ |
| 4 | Multiplication .* ; Right division ./ ; Left division .\ ; Matrix multiplication * ; Matix right division / ; Matrix left division |
| 5 | Addition + ; Subtraction - |
| 6 | Colon operator : |
| 7 | Less than < ; less than or equal to <= ; greater than > ; greater than or equal to >= ; equal to == ; not equal to ~= |
| 8 | Element-wise AND & |
| 9 | Element-wise OR | |
| 10 | Short-circuit AND && |
| 11 | Short-circuit OR || |
Since parentheses have the highest precedence level, parentheses are used to override the default precedence of all other operations.
©sideway
ID: 140400003 Last Updated: 4/8/2014 Revision: 0
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
