Content
MatLab: Scratch
Canvas &
Graphic
Operations
2D Plots
Line Graphs
Examples
3D Plots
MatLab: Scratch Canvas & Graphic Operations
Major Reference Source: MatLab Verson 7.0
Using MatLab package as a scratch canvas interactively is one of the common application of the MatLab package. MatLab commands are entered at the prompt command, >>, of the Command Window through the PC keyboard. Both entered commands and evaluation results are displayed in the Command Window. All new line or lines of commands or instructions after the prompt command will be passed to MatLab for evaluation after pressing the Enter key no matter the position of mouse cursor is at the end of line or lines or not. However, the MatLab package is design as a tool to manipulate data instead of a design tool to create some common features, therefore functions are usually some basic tools to present or display the provided data graphically in the scratch canvas as a figure. In other words, both the domain and range of the function are needed to be provided before a single graph of the function can be presented by a plotting function. As the plotting area is only be considered as a scratch canvas, multiple functions plotting on the same scratch canvas are allowed. Besides there are also addition tools for annotating and manipulating the figure in the scratch canvas.
2D Plots
There are five types of 2D presentation, namely, Line Graph, Bar Graph, Area Graph, Direction Graph and Scatter Graph. These 2D presentations are characteristic by its form of presentation.
Line Graphs
The presentation of plot is in the form of line, actually piecewise line. The matrix and array arithmetic includes seven types of operations:
| Function | Description |
|---|---|
| plot(x,y) | to present one group of 2D data set, y with respect to x, by joining pointwise data with line in linear scales for both axes. |
| plotxy(x1,y1,x2,y2) | to present Two different groups of 2D data sets, y with respect to x, by joining pointwise data with line based on two different y-axes and in linear scales for both axes. |
| loglog(x,y) | to present one group of 2D data set, y with respect to x, by joining pointwise data with line in logarithmic scales for both axes. |
| semilogy(x,y) | to present one group of 2D data set, y with respect to x, by joining pointwise data with line in linear scale for x axis and in logarithmic scale for y axis. |
| semilogx(x,y) | to present one group of 2D data set, y with respect to x, by joining pointwise data with line in logarithmic scale for x axis and in linear scale for y axis. |
| stairs(x,y) | to present one group of 2D data set, y with respect to x, by drawing a stair step starting from horizontal line between two consecutive pointwise data in linear scales for both axes. |
| contour(z) | to present one group of 3D data set, z with respect to x and y, by drawing contour lines according to the third dimension, data value z of pointwise data automatically with scale axes respect to the first two dimension, x and y index of pointwise data in linear scales for both axes. |
| ezplot(f1,f2) | to present the line plotting of a function expression within an automatically generated default domain. The function expression with f1 and f2 is used to represent two parametrically defined planar function fx(t) and fy(t) over thte default domain 0<t<2π. The function expression with f1 only is used to represent either an explicit function with respect to x over the default domain -π<x<2π or an implicit function of x and y over the default domain -π<x<2π and -π<y<2π. |
| ezcontour(f) | to present the contour lines plotting of a function expression within an automatically generated default domain. The function expression with f1 and f2 is used to represent two parametrically defined planar function fx(t) and fy(t) over thte default domain 0<t<2π. The function expression with f1 only is used to represent either an explicit function with respect to x over the default domain -π<x<2π or an implicit function of x and y over the default domain -π<x<2π and -π<y<2π. |
Examples

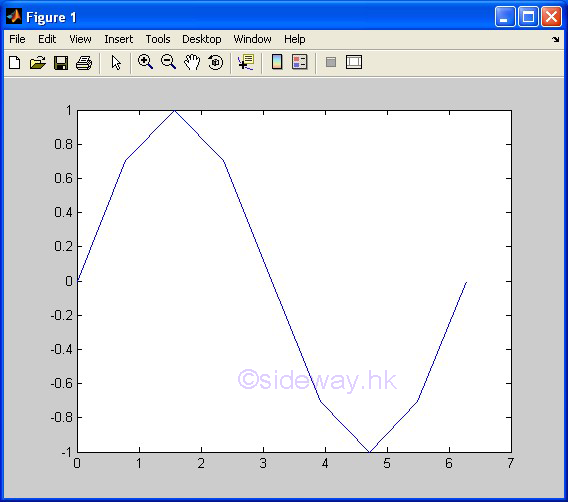
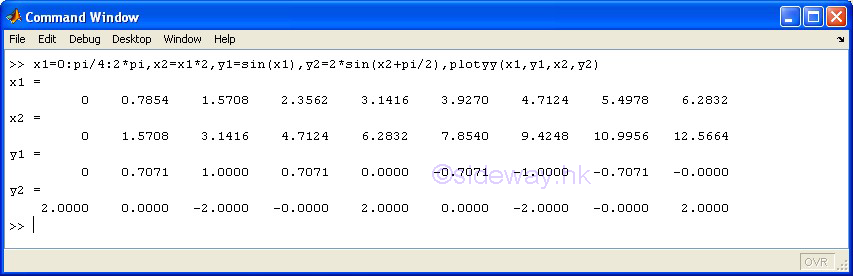
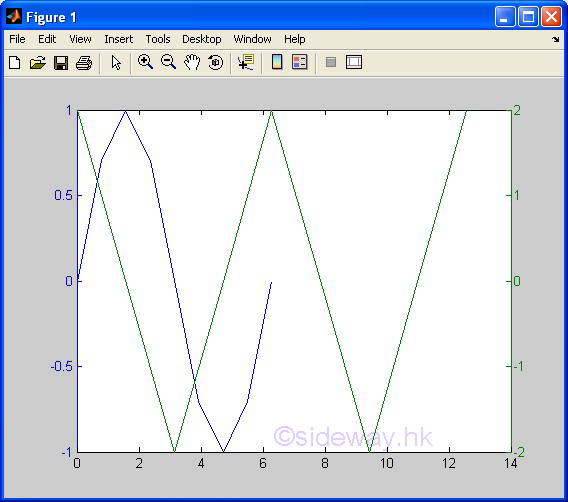
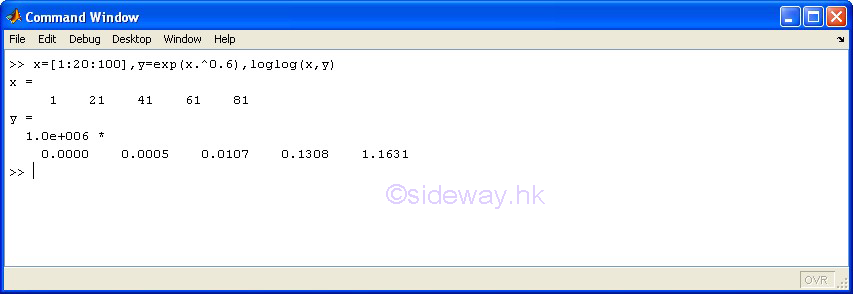
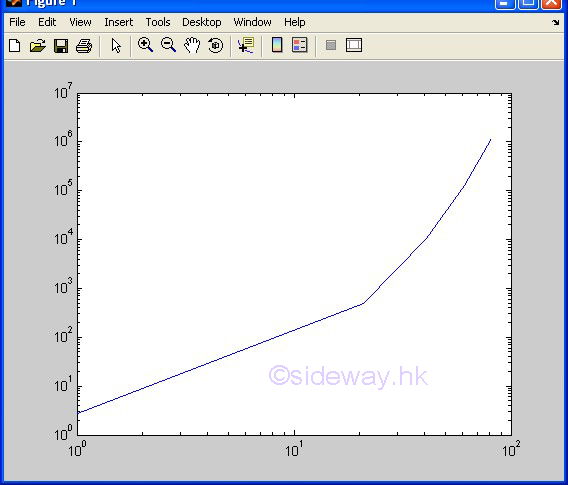
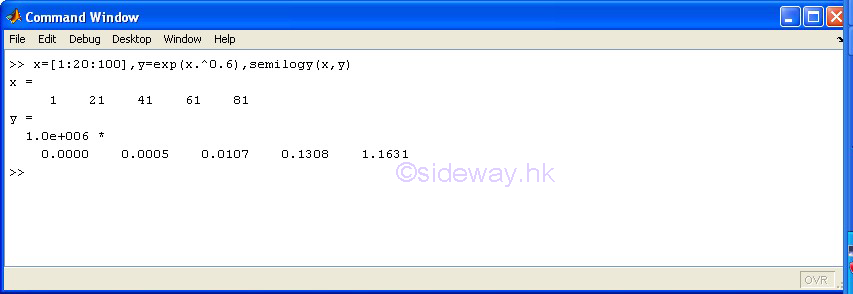
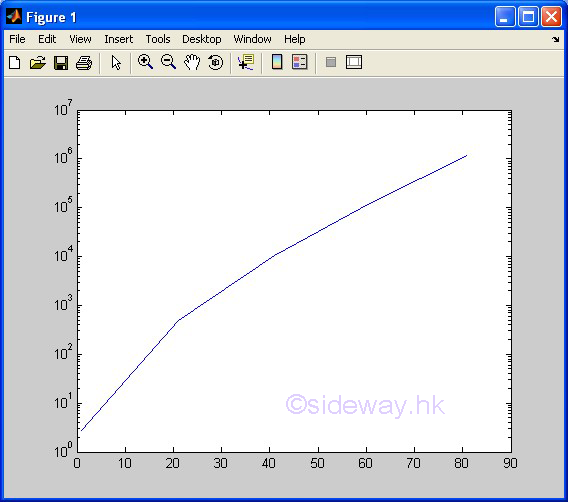
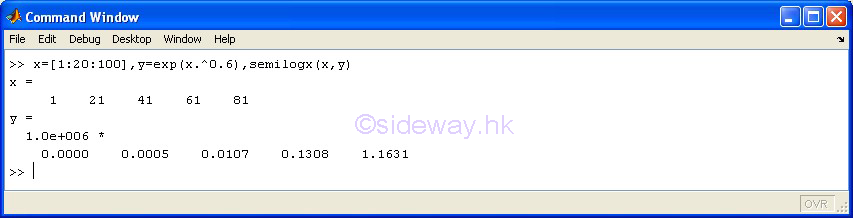
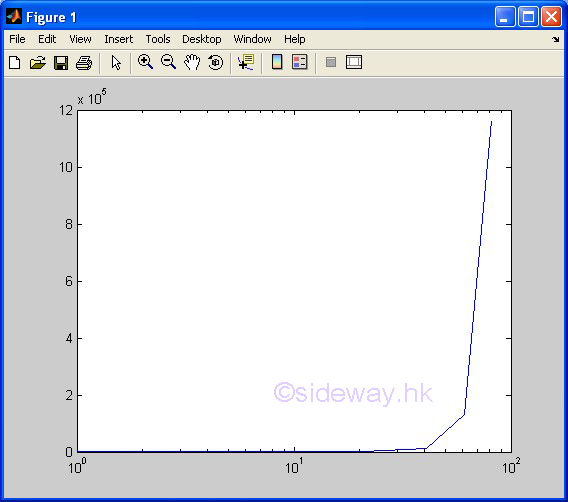
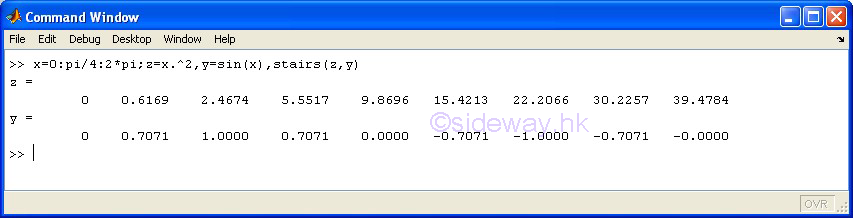
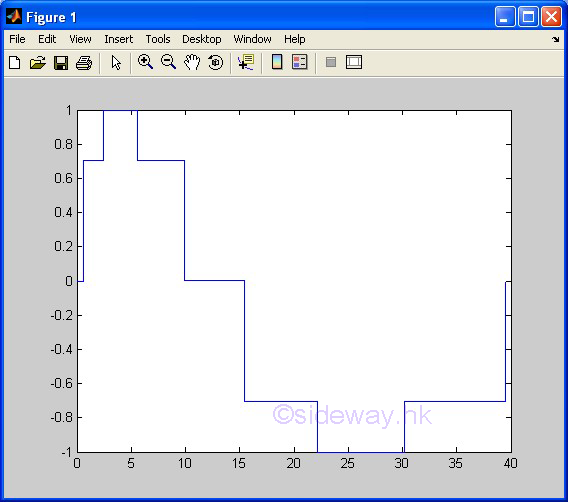
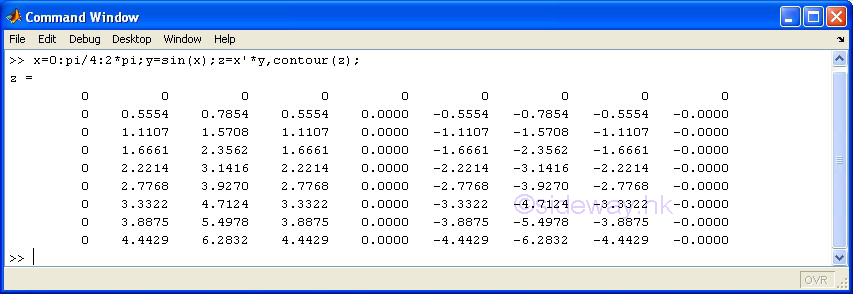
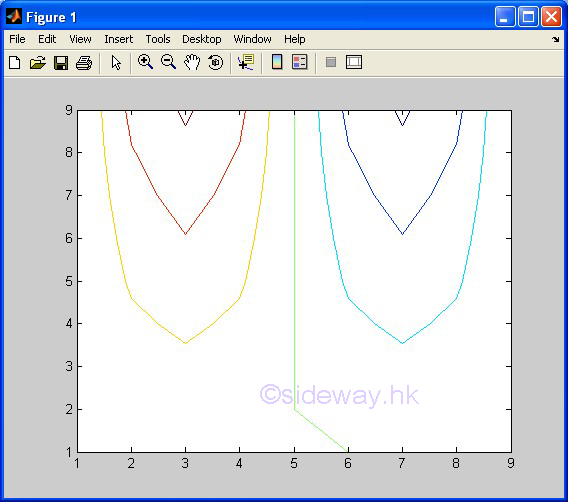

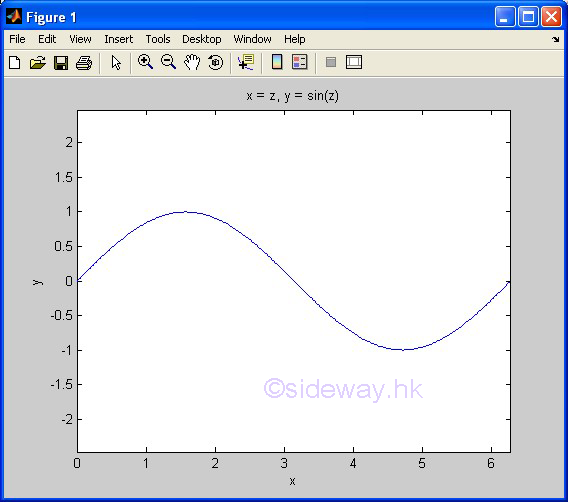
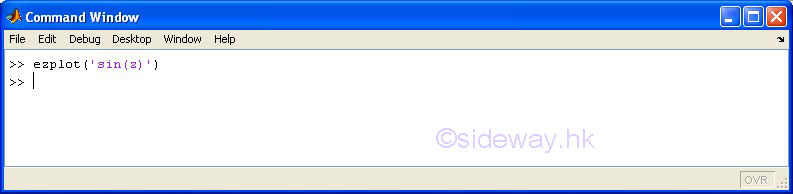
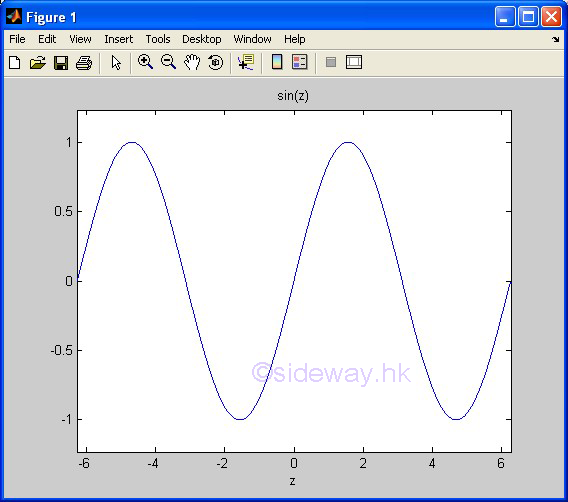
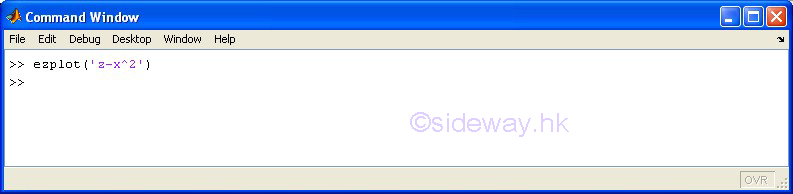
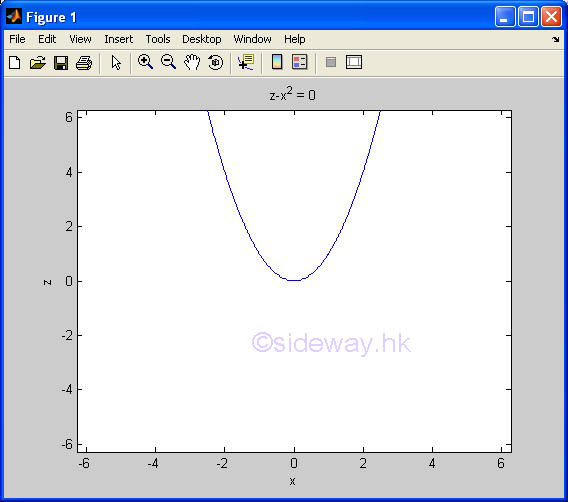

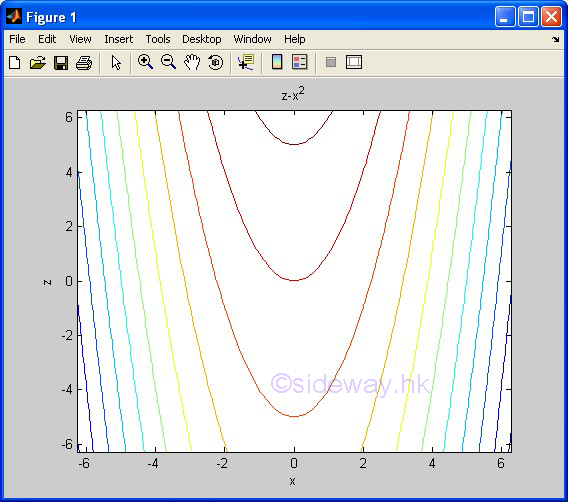
3D Plots
©sideway
ID: 140600009 Last Updated: 6/19/2014 Revision: 0
Latest Updated Links
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 33
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
