Content

Sound Physical Properties

In general, a sound wave propagates in all directions as a spherical wave. However when the sound source is very much far away from the receiver, the wavefronts of the spherical sound wave can be approximated by a plane wave wavefronts.  Since every neighborhood points of a plane wave wavefront are of same speed and direction, the behavior of any point on the wavefront can be used to estimate the physical properties of the whole wave front of a sound wave.

Reflection

When a sound wave hit a hard surface, the sound wave will change the propagation direction. The line of incident sound wave and the line of reflected sound wave form an angle and is bisected by the normal of the surface at the impact point.

Besides, only a portion of the acoustic energy can be reflected. A reflection coefficient is used to relate the ratio of reflected acoustic power to incident acoustic power as following 

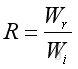
where

R is the reflection coefficient
W_r is the reflected acoustic power
W_i is the incident acoustic power

Absorption

When a sound wave hit a surface, part of the acoustic energy is absorbed and the other is reflected off. An absorption coefficient is used to relate the absorption coefficient with reflection coefficient and can be defined as:

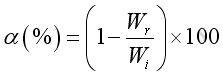
where

α is the absorption coefficient
W_r is the reflected acoustic power
W_i is the incident acoustic power

A material with zero absorption coefficient is an hard acoustic material with incident acoustic energy equals to reflected acoustic energy. A material with approximately 100% absorption coefficient is an soft acoustic material with very small portion of incident acoustic energy is reflected.

The absorption coefficient is sensitive to the frequency of the sound wave. For a high frequency sound wave with shorter wavelength, the penetrating power is much higher than that of low frequency sound wave with longer wavelength. A better penetrating power into the medium means more acoustic energy can be converted into heat energy. And therefore the absorption coefficient generally increases with frequencies.

Transmission

When a sound wave hit the surface of a wall, part of the acoustic energy is reflected or absorbed and the unabsorbed acoustic energy is transmitted to the other side of the wall. A transmission Loss (T.L.) is a common logarithm value used to relate the ratio of the incident acoustic power to the transmitted acoustic power in dB and can be defined as:

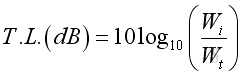
where

T.L. is the transmission loss in dB
W_i is the incident acoustic power
W_t is the transmitted acoustic power

A transmission loss of 0 dB implies all incident acoustic power are transmitted, e.g. open window. A sound wave with a transmission loss of 3 dB after passing through a material implies only half of the incident acoustic energy is transmitted.

Similarly, the transmission loss is also higher at higher frequency as the absorption is higher at higher frequency. But the transmission loss is also affected by physical structure of the medium, e.g. shape, dimension, and the characteristics of the incident sound wave, e.g. incident angle.

Diffraction

When a sound wave hit the edge of an obstacle, the sound wave around the edge will be diffracted. An insertion loss is used to measure the sound energy loss due to the installation of an obstacle and can be defined as:

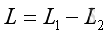
where

L  is the insertion loss in dB
L₁ is the sound level without obstacle at the receiver
L₂ is the sound level with obstacle at the receiver

Sound wave diffraction is also affected by the sound wave frequency. Low frequency sound waves of long wavelength are less affected by the obstacle than high frequency sound wave of short wavelength. When the obstacle dimensions are smaller than the wavelength, the edge of the obstacle acts like a virtual source and bypasses the obstacle. As a result, a complete acoustic shade cannot be achieved behind a noise barrier.

Therefore, the bass contents of a music is always the dominating portion for a receiver behind an obstacle over the treble contents. Or the noise barrier of a highway for a low frequency heavy truck noise are also less attenuated than noise from a private car or high frequency tire squeal.