Content
Moment Vector
Couple Vector
Couple Vector Decomposition
Couple Vector Addition
Moment Vector
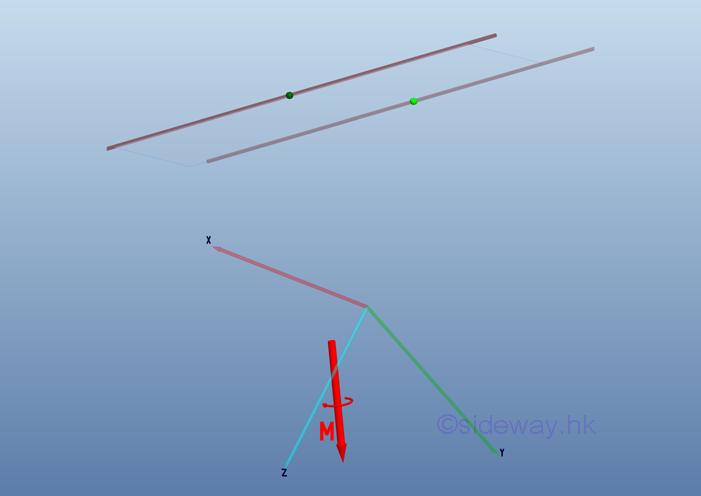
The only effect of a force couple on a rigid body is the moment of the couple because the net force on a rigid body is zero. A moment vector M according to the right hand rule can be used to represent the magnitude and direction of the effective moment of a couple.
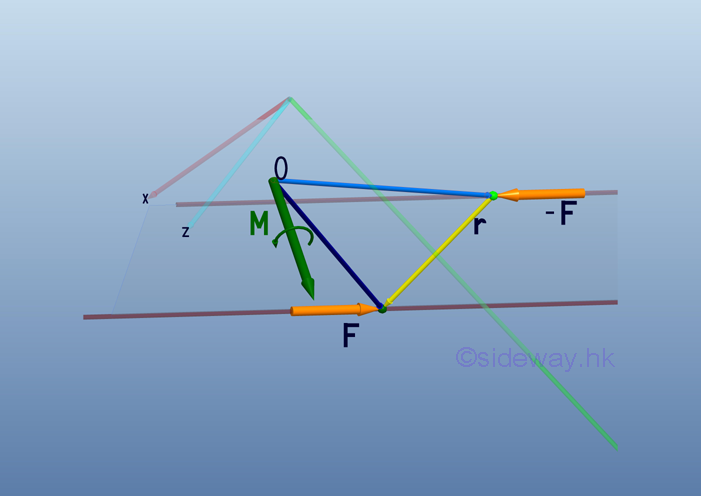
However, a moment vector M can not be used to represent a couple because a moment vector always refer to a reference point while the effective moment of a couple is a free vector in space.
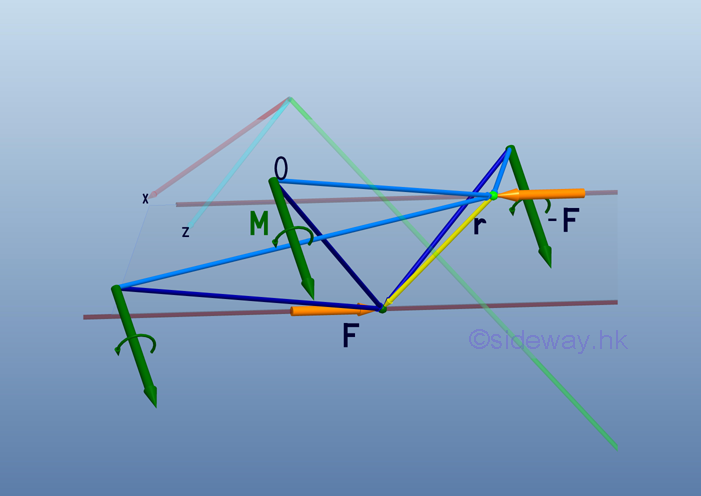
Couple Vector
The moment M of a couple is the only thing to determine the equivalent of two couples. Through couple transformation, equivalent couples with different location of application, and different magnitude and direction can have the same effect on the motion of a rigid body. Imply all equivalent couples produce same moment effect at the same reference point.
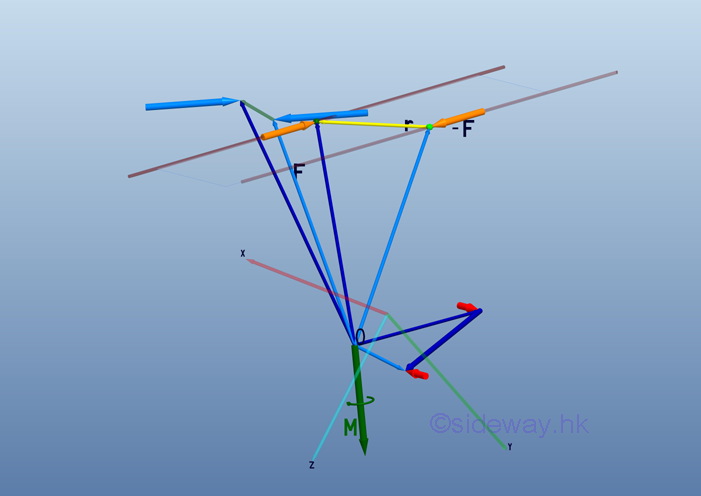
Couple with the same moment of equal magnitude and direction will produce the same effect on the motion of rigid body. Similar to moment vector, a couple vector M can also be used to represent the sense of rotation, and the magnitud and direction of a couple itself. Unlike the moment vector, the couple vector is used to replace the force couple. Imply all equivalent couples can be replaced by the same couple vector.
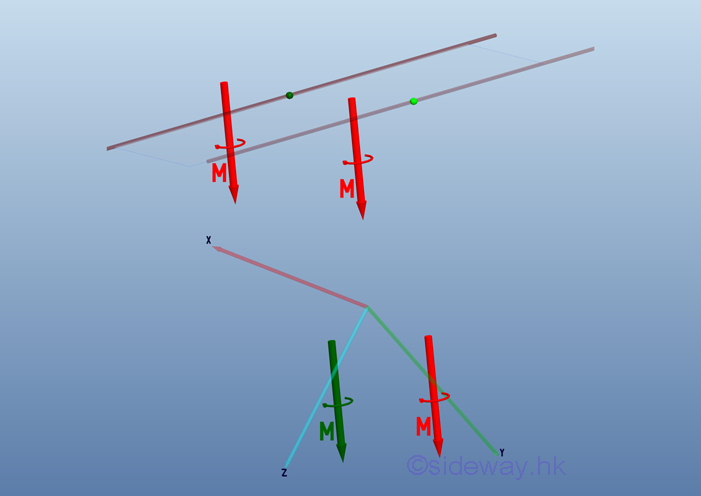
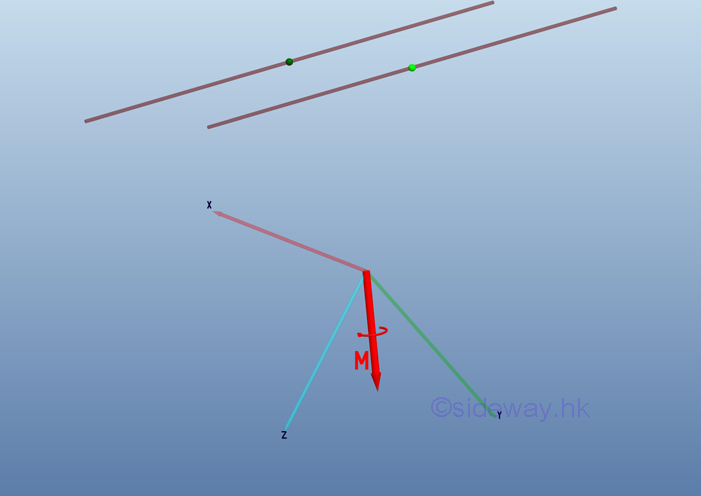
Since equivalent couples are independent of point of application, and magnitude and direction, a couple vector M is a free vector. As a force couple with same moment can be transformed freely in space, the moment vector or the moment effect about a reference point can be replaced by a force couple or a couple vector with the magnitude and direction of a couple vector equal to the moment vector. And because the net force of a force couple is zero, the resultant force acts at the reference point on the rigid body is zero also. Imply the moment vector M of a force couple can be replace by a couple vector M .
Besides a couple vector is a free vector, it can be translated to the origin of the coordinate system also.
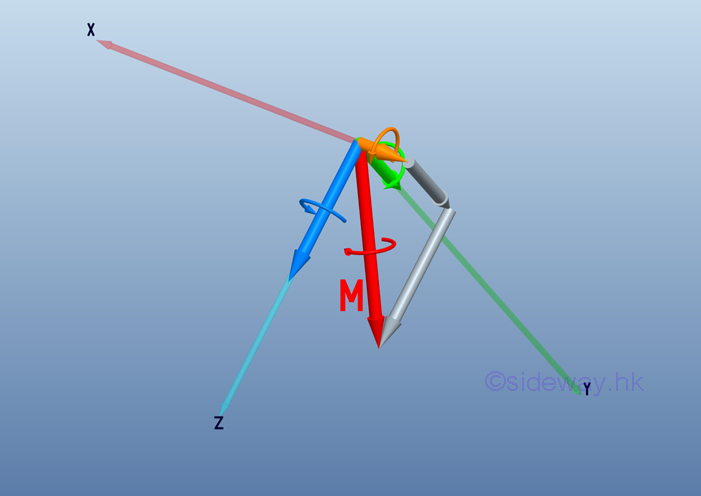
Couple Vector Decomposition
When considering force couple decomposition, the points of application will affect the formation of the three rectangular components. But for the decomposition of couple vector, the couple vector M can be resolved into three rectangular vector components along the coordinate axis Mx , My and Mz like other rectangular vector decomposition.
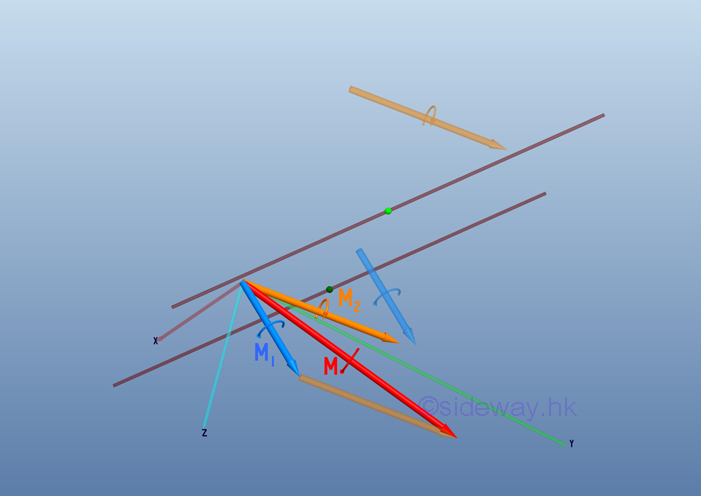
Couple Vector Addition
The addition of force couple involves the transformation of force couple. By making use of the free property of couple vector , the resultant couple vector can be determined by simple vector addition in space.
©sideway
ID: 110700006 Last Updated: 7/6/2011 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Space(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight AltitudeX(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 31
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
