Content
Distributed Force
Body Force:
Distributed Load:
Distributed Force
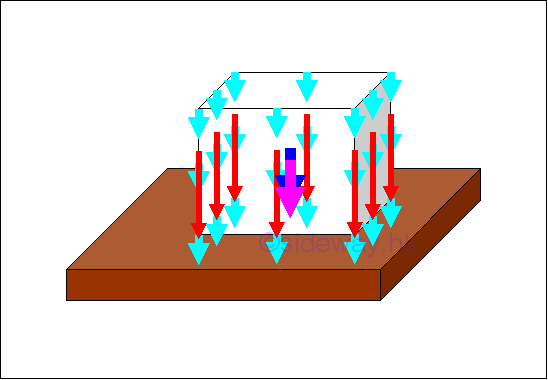
A force acting on a point along a single line in space is a concentrated force. A concentrated force is the mathematical idealization of forces in practical problems, in which all forces are either body forces acting over a volume or surface forces acting over an area. These types of forces are called distributed forces which are either distributed over a specific volume or spread out over a specific area. Through system of forces transformation, the distributed forces can be represented by a concentrated force.
Body Force:
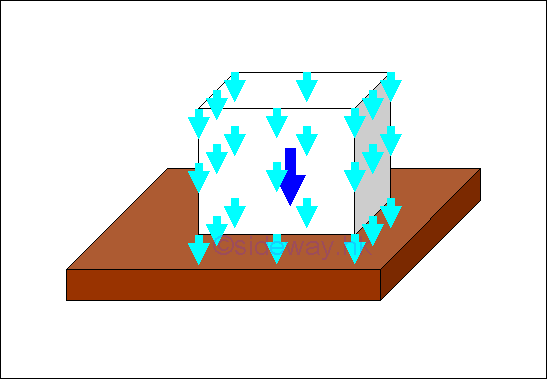
In static mechanic, a body force is the attraction force exerted by the earth on a rigid body. The attraction force is called the force of gravity or in general, the weight of the rigid body. The force of gravity acts on each of the particles of the entire body. Therefore the gravitational forces of a body can be represented by numbers of small gravitational forces distributed over the body volume. In mathematical idealization, the gravitational force of the body is represented by a resultant force acting on the center of gravity of the body as the weight of the body.
The center of gravity of a body is related to the gravitation attraction, density and shape of the body. For an uniform gravitational force field, the center of mass of a body is equal to the center of gravity of a body. And in practical problems, the center of gravity is sometimes also refered to the center of mass. For a homogeneous body with constant mass density, the centroid of the shape of a body is equal to the center of gravity. Imply
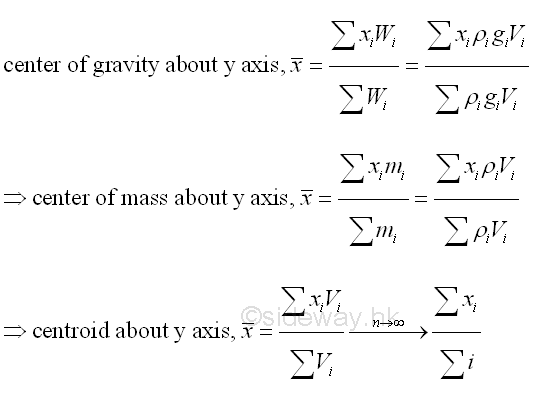
Distributed Load:
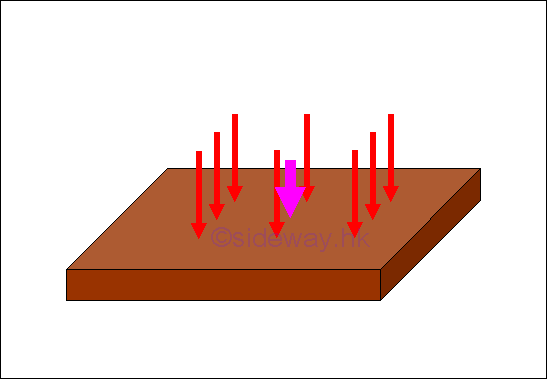
Similarly, many mechanical structures are subjected to distributed loads spread out over a specific area rather than concentrated loads in static mechanic. However, an equivalent normal concentrated force is often used to represent the applied distributed loads spread out over a specific area when solving practical problems.
For an uniform distributed load, a load of constant magnitude is applied over a specific area. The resultant of these distributed loads can be represented by a normal concentrated load with magnitude equals to the sum of the distributed loads or the product of uniform distributed load per unit area and the applied area, acting on the center of gravity or center of mass, or center of centroid of the applied area of applied load.
In general, the magnitude of the equivalent normal concentrated load for the resultant force of a distributed load is equal to the summation of the all distributed forces or the area under the function of the distributed load. And the applying position of the equivalent normal concentrated load can also determined by taking moment about a pont or an axis as in body force. For example, a distribution load of load distribution function, D(x) spread on a beam along x axis, imply
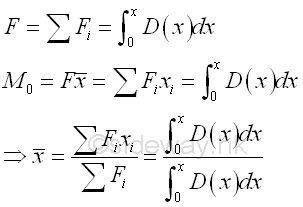
©sideway
ID: 120300021 Last Updated: 3/28/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Mandai(last updated On 12/8/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/7/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 24
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
