Content
Distributed Loads
Distributed Load on beam
Uniform Distributed Load on Beam
TriangularDistributed Load on Beam
Composite Distributed Load on Beam
Distributed Forces on
Elevated Surface or Submerged Surface
Wind Load on Tall Building
Hydrostatic Force on Rectangular Submerged Surface
Hydrostatic Force on Curved Submerged Surface
Distributed Loads
Distributed loads are applied forces acting on a body. Physically, distributed loads can be divided into discrete distributed forces and continuous distributed loads. A discrete distributed forces is a set of concentrated foces as point loads acting on the body. And the system of forces of a discrete distributed forces can be simplied into one single concentrated force through system of forces transformation. But in practical mechanical applications, a continuous distributed forces acting on the body can be considered as a continuous force function.
The concept of finding the centroid of an object can also be used to determine the equivalent concentrated force of a distributed load acting on a system for calculating the reactions, not the internal forces and deflections. Therefore besides determining the equivalent concentrated force by integration, the equivalent concentrated force can also be determined by making use common functions of shapes or the decomposition of composite shape into simple shapes.
Distributed Load on beam
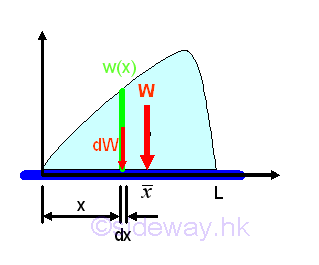
Assume the distributed loads can be expressed as a function in terms of x, i.e. w(x), per unit length, the total distributed load can be determined by integration.imply
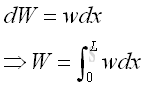
If the distributed load is homogenous, then the distributed load can be expressed in terms of area. Imply
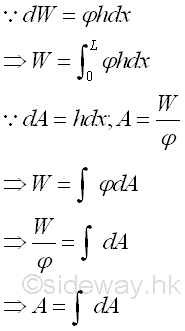
By the first moment of weight or area, the position of the application of the equivalent concentrated load W is
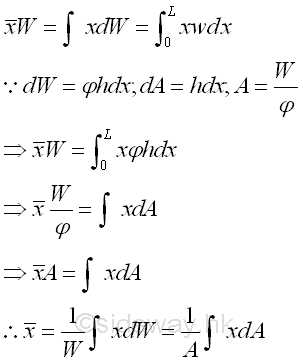
Uniform Distributed Load on Beam
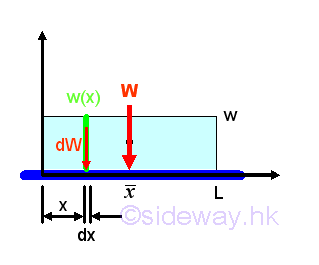
Let the uniform distributed load per unit length is equal to w. And for a uniform distributed load, the total distributed load W is equal to
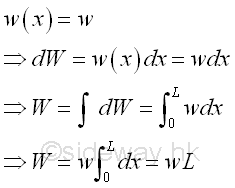
By taking the first moment of weight or area about origin, the position of the application of the equivalent concentrated load W is
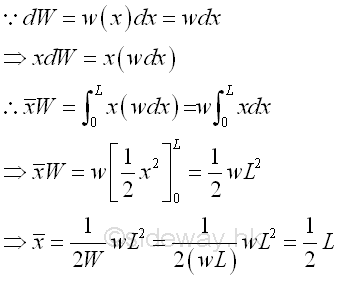
TriangularDistributed Load on Beam
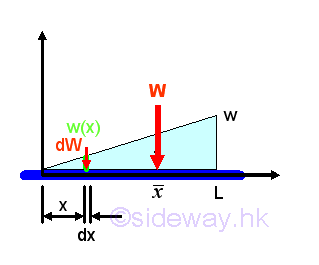
Let the maximum distributed load per unit length is equal to w. And for a triangular distributed load, the total distributed load W is equal to
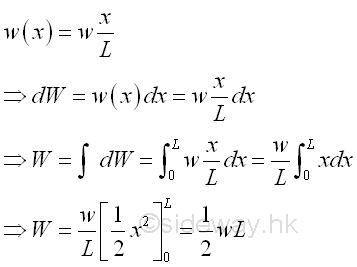
By taking the first moment of weight or area about origin, the position of the application of the equivalent concentrated load W is load W is
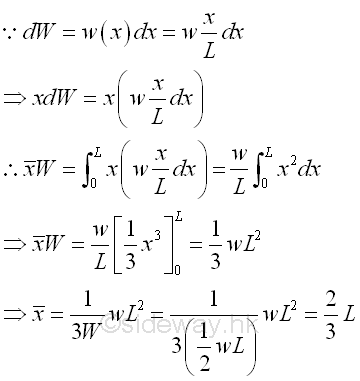
Composite Distributed Load on Beam
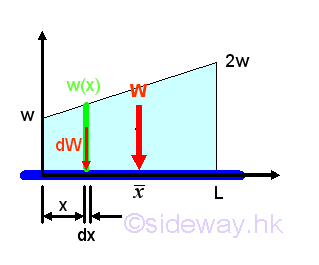
Let the minimum distributed load per unit length is equal to w, the maximum distributed load per unit length is equal to 2w. And for a composite distributed load, the total distributed load W is equal to
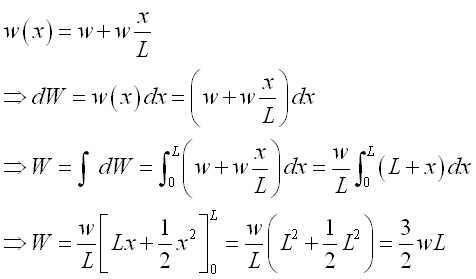
By taking the first moment of weight or area about origin, the position of the application of the equivalent concentrated load W is
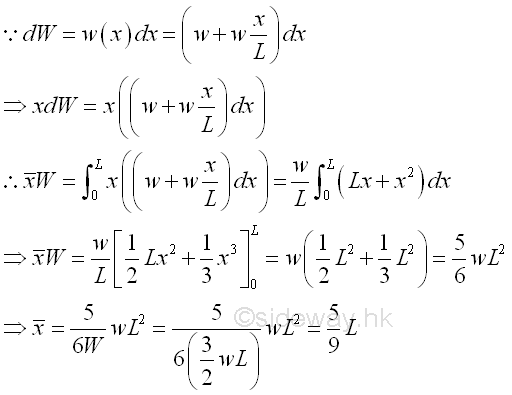
Distributed Forces on Elevated Surface or Submerged Surface
Two most common practical applications are the wind loads acting on tall elevated building and the hydrostatic pressure forces exerted on the surface submerged in a liguid.
Wind Load on Tall Building
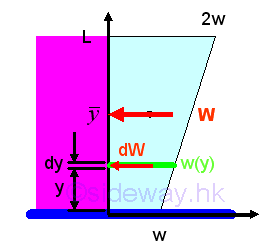
The force exerted on a rectangular tall building due to the wind current acting on the surface can be modeled as a linear distributed load. Let the minimum distributed load per unit length is equal to w, the maximum distributed load per unit length is equal to 2w. And for a composite distributed load, the total distributed load W is equal to
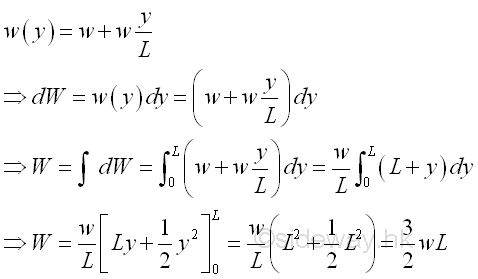
By taking the first moment of weight or area about origin, the position of the application of the equivalent concentrated wind load W is
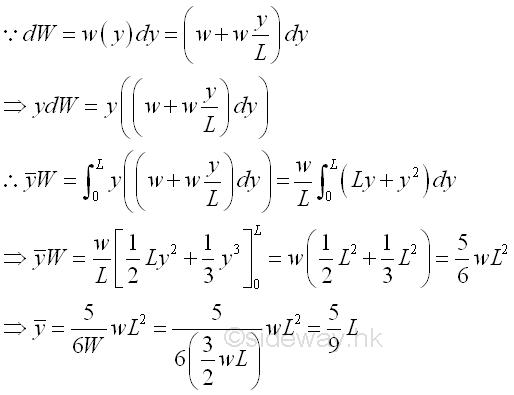
Hydrostatic Force on Rectangular Submerged Surface
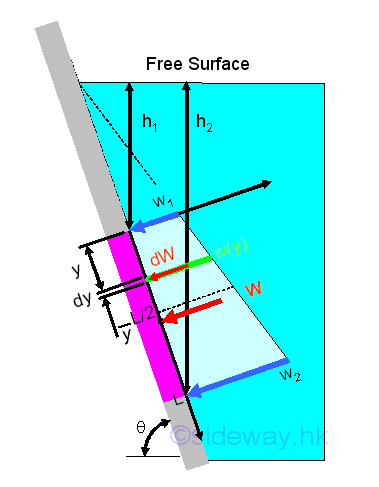
When a fluid is at rest, the hydrostatic force acting on the boundary must be normal to the surface of the boundary. For a submerged thin rectangular plate with length L and width b in a liquid, the elemental hydrostatic force due to the hydrostatic pressure p, gauge pressure, is pdA or pbdx. Since the gauge pressure at the level of the elemental surface in a liquid can be expressed in terms of the depth of the elemental surface below the free surface, i.e p=ρgh. assume b=1. Imply
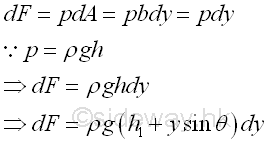
The resultant force acting on the rectangular plate can be determined through the decomposition of the resultant force due to the hydrostatic pressure distribution into the rectangular and triangular components.
The rectangular componment FR of the resultant force is
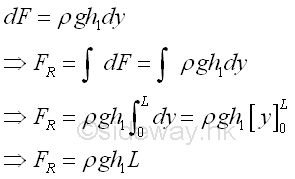
The triangular componment FT of the resultant force is
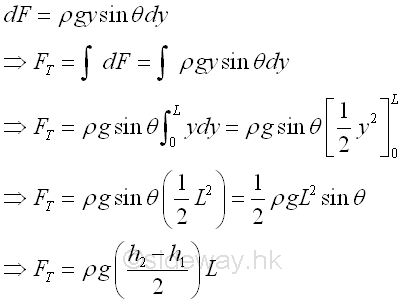
The magnitude of the resultant force F is
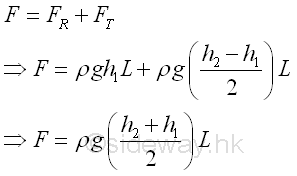
Since the vertical locations of the rectangular and trianglar components of resultant force are applied at the centroids of the rectangular and trianglar components accordingly. The location of the resultant force F along y axis can be determined by taking moment about upper edge of the rectangular plate. Imply
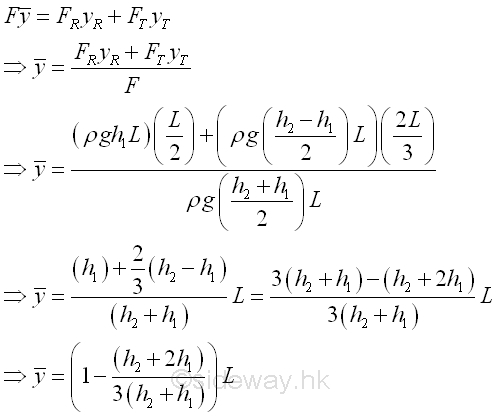
Hydrostatic Force on Curved Submerged Surface
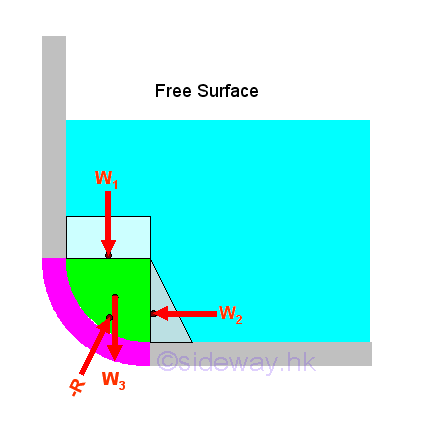
The resultant force acting on the curved surface can be determined through the decomposition of the resultant force due to the hydrostatic pressure into the rectangular component w1 and the triangular component w2 and the weight of the detached volume of the liquid w3 .
Therefore the magnitude of total vertical force FV and total horizontal force FH acting on the curved surface are
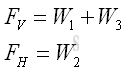
And the resultant force R acting on the curved surface is
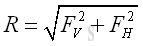
The magnitude of forces, w1 , w2 and w3 can be determined by the hydrostatic pressure similarly. And the location of equivalent system of forces by solving the equilibrium equation of moment about an axis.
©sideway
ID: 120700005 Last Updated: 7/14/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 22
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
