Content
Equilibrium of Rigid Body
Free-Body
Free-Body Diagram
Equilibrium of Rigid Body
A rigid body is in static equilibrium state when the rigid body remains stationary and is not accelerating in any way. In other words, a rigid body is in equilibrium when both the resultant force and the resultant moment are zero for all the forces and couples acting on it. Through system of forces transformation, an equivalent system of forces can be reduced to a force vector and a couple vector. Therefore the resultant force and the resultant couple vectors acting on the rigid body are equal to zero. That is:
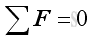 and
and
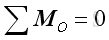
Or in terms of rectangular components:
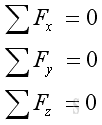 and
and
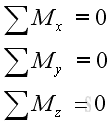
In other words, there is no translational and rotational motion when an object is in static equilibrium state.
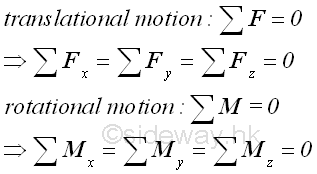
Free-Body
In engineering static application, a rigid body is in equilibrium when the systems of external forces cause no translational and rotational motion to the rigid body since the resultant force and resultant memont on the rigid body are zero. For example, a hanging mass from the ceiling
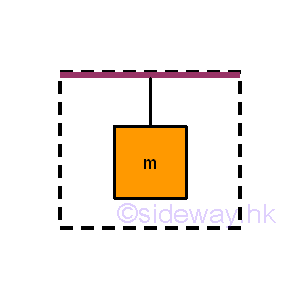
When solving the equilibrium problem of the considered body, in order to focus only on the interested body instead of the whole system, the interested body should be isolated from other bodies as a free body. According to Newton's third law, each applied force will have a reaction force of equal in magnitude and opposite in direction acting on the interacting bodies. Therefore, all the surrounding uninterested objects can be stripped away by replacing with the corresponding reaction force acting on the interesed body. For example, the interested objects are the mass and string.
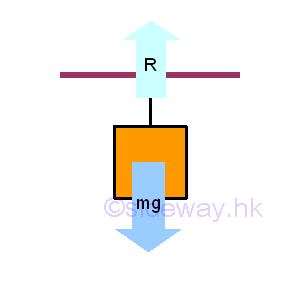
Therefore, a free body diagram can be drawn by adding a reaction force to replace the force due to the ceiling, while the body force due to the body mass remains unchange.
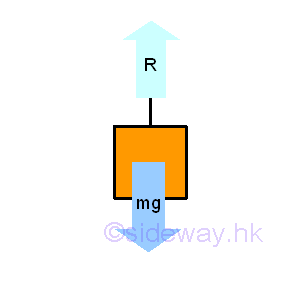
Since the hanging string is also not an interested body, Imply the free body diagram of the body mass is :
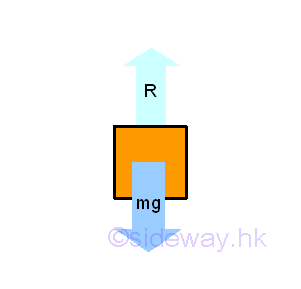
Free-Body Diagram
Important steps of constructing the free-body diagram are:
-
Selecting the interested bodys from the whole system, so that the free body of interest can be detached away from the ground, connections, supports and all other bodies.
-
In general, there are always forces exerted on the free body by those stripped away bodies. These forces are considered as external forces and are represented by forces acting on the free body.
-
Besides, the weight of the free body should also be considered and be included as external forces acting on the free body.
-
But for forces exerted on each other between various parts of the free body, these forces are considered as internal forces because the free body is considered as a rigid body also.
-
For known external forces, such as weight of free body, applied forces, both the magnitudes and directions of each known external forces should be marked at the corresponding position on the free-body diagram.
-
For those unknown external forces due to stripping away bodies, such as ground, connections, supports and all other bodies from the free body, these forces are usually the reaction forces to opposite the motion of the free body in order to constrain the free body to remain in the same static position. Each known external forces should also be marked at the corresponding position on the free-body diagram. Although the magnitudes of unknown external forces are unknown, the reaction directions of each unknown external forces at the supports and connections can usually determined by its type of support or connection.
-
The pointing direction of an unknown external forces after the avaialable reaction are determined can be assumed in any direction because the sense of the direction will confirm whether the assumption is correct or not.
- Although, the profile of the free body can usually be neglected, the free-body diagram should include dimensions for calculating the moments of forces.
- Finally, including a coordinate axis is also necessary for determining the sign and angle of forces
©sideway
ID: 120200059 Last Updated: 2/15/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight River Wonders(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)
- Travel Singapore Sight Night Safari(last updated On 12/30/2025)
- Travel Singapore Sight Curiosity Cove(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 37
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
