Content
Virtual Work
Work of a Force
Work of a Couple
Principle of Virtual Work
Virtual Displacement
Application of Principle of Virtual Work
Mechanical Efficiency
Virtual Work
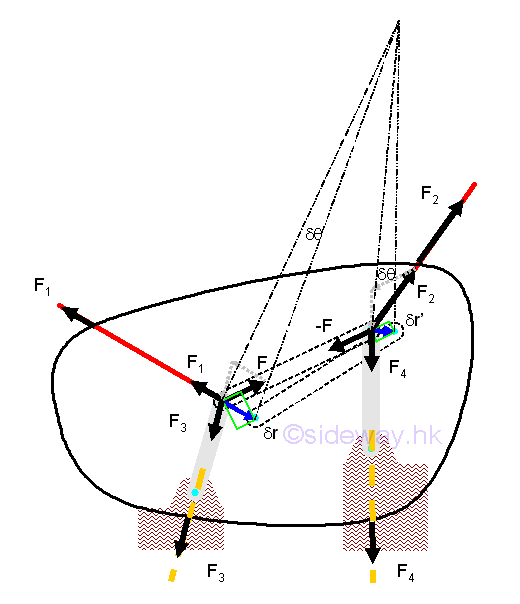
The unknown force acting on a rigid body is usually solved by balancing the external forces and moments acting on the body and solving a system of simultaneous equations using the equilibrium state of the rigid body. In mechanic, work is the displacement of a body done by a force or a moment. If there is no displacement of the body, then no work is done by a force acting on the body. By applying the principle of virtual work, used by Jean Bernoulli, the total virtual work of a body or a system of connected bodies in equilibrium is equal to zero. Therefore unknown force can be determined by applying a virtual displacement to the system of connected bodies.
Work of a Force
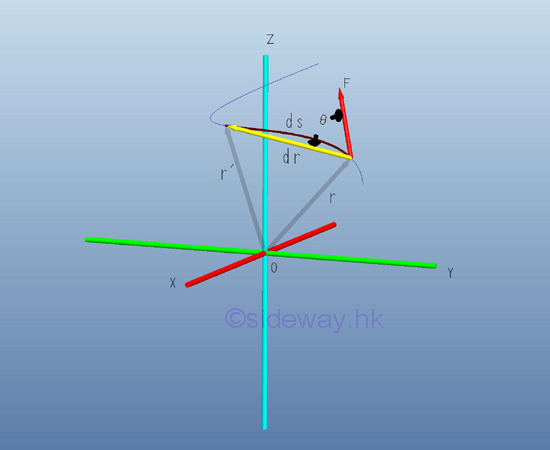
By definition, work is done by a force when there is a displacement at the point of application in the line of action of the force with magnitude equal to the product of the applied force and the linear displace along the line of action of the force. A displacement is the change of the position. A displacement of a body is the linear displacement of the body. An angular displacement is the change of the orietation by means of rotation. Although a finite angular displacement is not a vector quantity, the travelled distance due to an infinitesimal angular displacement can be used to approximate the corresponding displacement vector quantity. Therefore an infinitesimal work done by a force acting on a body with an differential displacement can be expressed as the scalar product of the force vector and the displacement vector. Imply
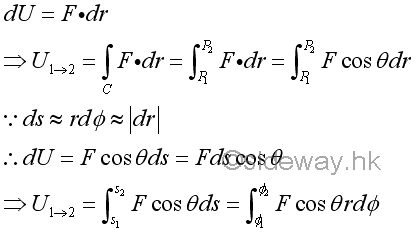
In general work done by an applied force is dependent on the path C travelled. But for a conservative force, the total work done by a conservative force only depends on the displacement and is independent on the path C travelled. And for a non-conservative force, like friction, the total work done is dependent on the path travelled. However, the work done by an applied force undergoes infinitesimal angular displacement can be approximated as the work done by an applied force undergoes a linear displacement vector quantity.
By definition, the scalar product of two vectors is a scalar quantity of no direction with magnitude and sign only. Since the angle between the force vector and the displacement is from 0≤θ≤180o , the value of work done is negative when the angle is 90o<θ≤180o . And if the force vector is perpendicular to the displacement, i.e angle=90o , then no work is done.
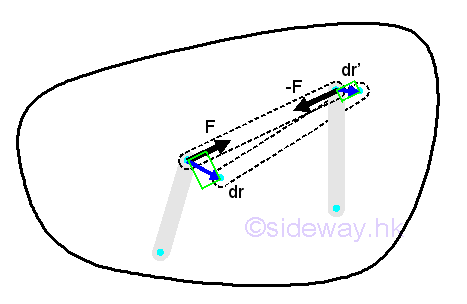
When a rigid body or a system of rigid connected bodies is in equilibrium, both the external forces and the internal forces are in equilibrium. Besides, the total work of the internal forces is equal to zero also. For example, by imagining two points in a rigid body is connected by a link under two equal and opposite forces F and -F along the link. Although the displacement dr and dr' can be different, the components of these displacements along the axis of link must be equal because the distance between the two points must remain at the same distance from each other while moving by the forces.
Work of a Couple
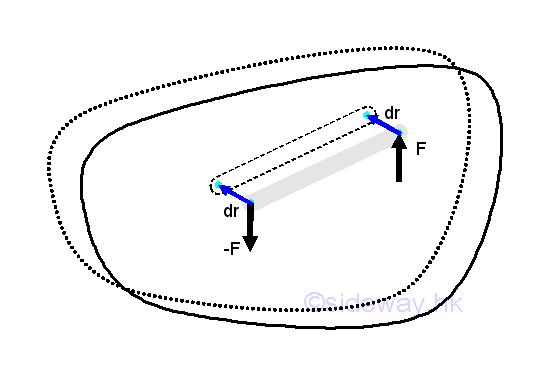
If a rigid body is under a translation motion, the total work of a couple of forces acting on the rigid body is always equal to zero because there is no change in the orientation of the rigid body and the displacement of the particles are the same while the forces of a couple is always equal in magnitude and opposite in direction. Imply
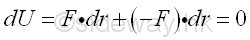
However, when the couple of forces acting on the rigid body causes an infinitesimal angular displacement parallel to the applied forces couple, the total work of the couple of foces is then not equal to zero.
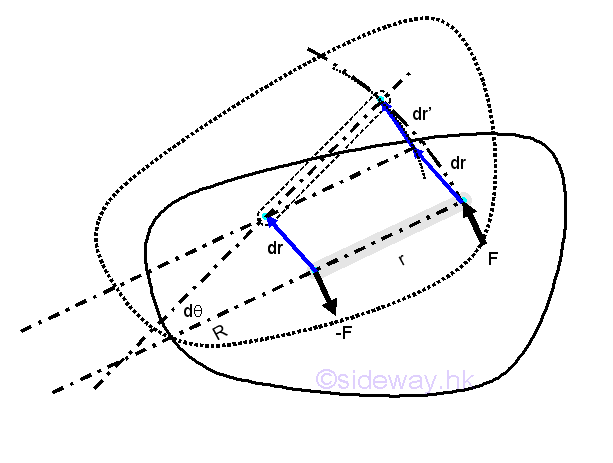
The work of the force F can be divided into two parts, therefore the total work of a couple of forces is
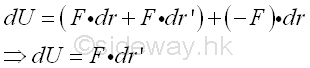
Since the forces F and -F are always tangent to the arcs of rotation at the point of the application of force accordingly, therefore the total work of the couple of moment is
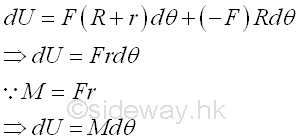
Similar to the work of a force, the instantaneous moment of the couple and the infinitesimal angular displacement should be in parallel, the work of a couple can be expressed as the dot product of two vector. Imply
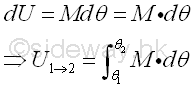
And therefore the work of a couple is equal to zero if the moment vector is perpendicular to the infinitesimal angular displacement. And if the moment M acting on the rigid body is a constant and the finite angular displacement Δθ is in the same direction as the moment during the angular rotation in radian. Imply
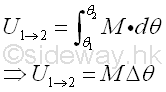
Principle of Virtual Work
Virtual work is the virtual displacement of a body done by a force or a moment acting on it. A displacement is the actual change of the position, while a virtual displacement is an imaginary differential displacement of a possible virtual displacement under actual displacement motion. And there are also linear and angular displacements. In other words, a possible virtual displacement acts as the simulation of a possible actual motion of the considered body under a first order differential displacement, at which the actual motion is possible to be performed. For example, a pinned linkage allows angular displacement while a weld linkage is fixed. Since the possible virtual displacement is to evaluate the work due to virtual displacement under the equilibrium state of the considered body, the possible compatible virtual displacement does not necessarily to be conformed to the constraints of the connections and supports of the considered body, because the constrains are already represented by the force vectors, which are used for the evaluation of the total virtual work of interested forces of the considered body under possible virtual displacement. Therefore both compatible with constrained virtual displacement or compatible virtual displacement can be used for detemined the virtual work. Usually, the virtual displacement is of first order accuracy with the second-order quantity can be neglected.
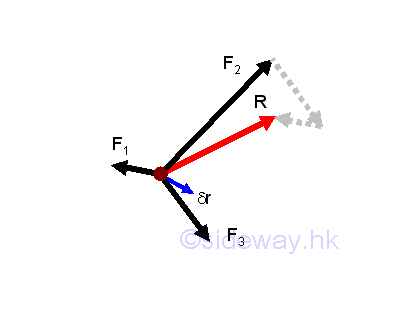
Consider a virtual displacement of a particle, the virtual work of the particle done by forces acting on the particle will be equal to the sum of the virtual work done by each force. And therefore the total virtual work δU done on the particle is equal to the virtual work δU done by the resultant force R. Imply
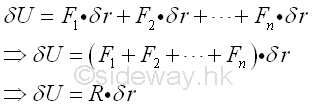
Therefore if the particle is in equilibrium, the resultant force R should be equal to zero, and the work done by the resultant force on the particale is equal to zero also.
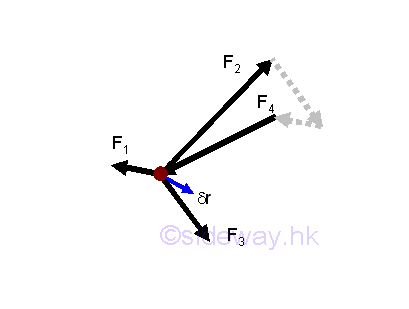
In other words, when the work done on a particle is equal to zero for any virtual displacement δr, the particle must be in equilibrium or R is equal to zero. Imply
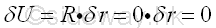
Or, when a particle is in equilibrium, the total virtual work done by forces acting on the particle is zero for any virtual displacement of the particle because the resultant force acting on the particle is zero when the particle is in equilibrium.
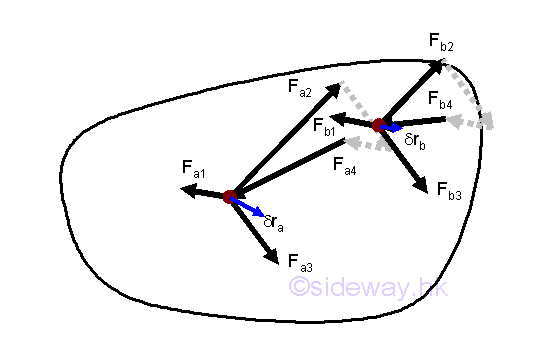
Since when a body is in equilibrium, all particles of the body must also be in equilibrium. Therefore the total virtual work done by forces acting on a particle is equal to zero when the particle is in equilibrium, the total virtual work done by all external and internal forces acting on all particles of the body for a compatible virtual displacement must also be zero when the body is in equilibrium. As the body is in equilibrium, the total virtual work done by all internal forces acting on all particle is zero, the total virtual work done by all external forces acting on the body must be zero also.
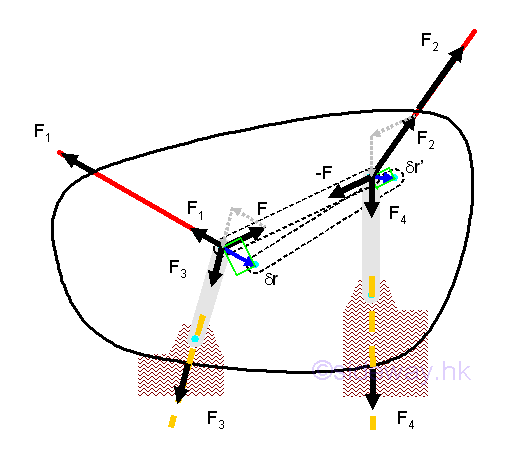
Therefore the principle of virtual work in static is the making use of the property of total virtual work, which is equal to zero, for an equilibrium free body. When a body is in equilibrium state, the system of external forces acting on a free body is in equilibrium, and the total virtual work done by the system of external forces acting on the free body for a compatible virtual displacement is equal to zero. The free body can be a particle, a rigid body, a connected particles and a conneced rigid bodie, e.g. frame, machine.
Virtual Displacement
Since the constraints provided by supports and connections in static equilibrium are used to define the reactions acting on the interested free body only, the virtual displacements of a free body are not limited by the constraints. However the virtual displaements of a free body are limited by the reaction forces acting on the free body and the compatibility of the allowable motions of the free body. Therefore virtual displacement of a body is an imaginary set of compatible differential displacements of first order with fixed relation in equilibrium state.
For a first order accuracy differential displacement of a body, the
second-order quantity can be neglected. The virtural linear displacement of the
acting points on the free body can be related to a virtual angular displacement
of the body which is assumed to be a rotation of the free body or the components
of the free body about a displacement center. The relation between the virtual
linear displacements of points on the free body can be determined approximately
geometrically. For example, a ladder of length, l leans against a wall at an
angle of θ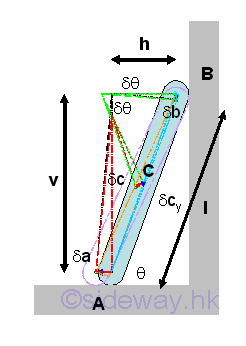
Since the positions of points A, B, and C are fixed, the displacement centres of
A and B, C and A, and C and B can be found by constructing the radius of
rotation and therefore the relation between δa and δb, δc and δa, and δc and δb
can also be determined accordingly. But the vertical component δcy of virtual
displacement δc can be obtained by making use of the proportional
parts of similar triangles approximately. And the horizontal component δcx can also be determined similarly. Imply
Besides the method of displacement centres, the relation between two virtual displacements can also be determined using differential calculus. Geometrically, the positions of points A and B can be expressed in term of the length, l of ladder and the leaning angle, θ. Therefore the virtual differential displacements can be obtained by differentiation. And the relation between two virtual displacements can then be obtained by equating the two relations. Since the horizontal distance is in negative sense, imply
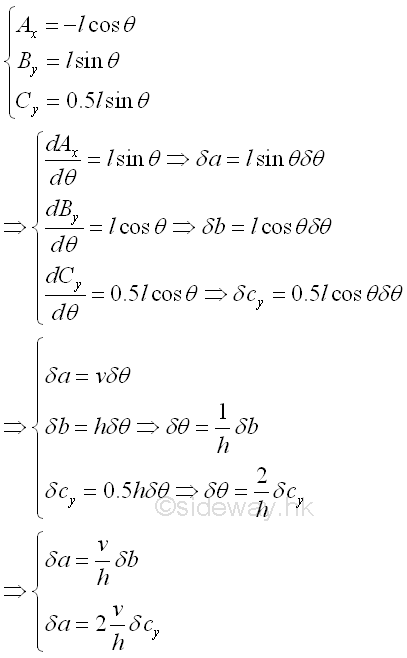
Application of Principle of Virtual Work
Instead of solving the simultaneous equations of complex frame and machine
problems, these complex equilibrium can also be determined by applying the
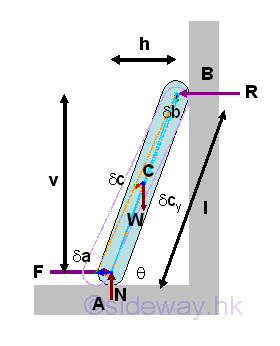
principle of virtual work. For example, in the ideal case with smooth wall, the
friction force F required to retain
the ladder of weight W in position can be determined by the principle of virtual
work. Since a virtual counter-clockwise angular displacement along with the angular
dimension, θ is in positive sense, the virtual clockwise angular
displacement implies a negative sense of the virtual displacements. Therefore
the sense of virtual displacements are determined by the virtual angular
displacement. Imply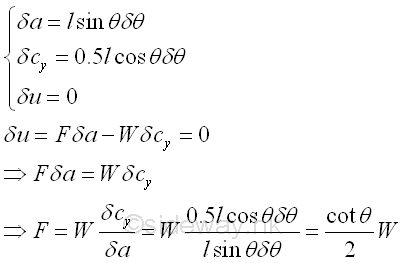
Or, by solving the equilibrium equations of the free body simultaneously. Imply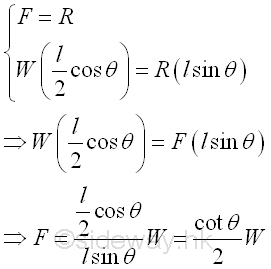
Therefore, if the relation of the virtual displacements of the interested forces can be obtained, the interested force can be determined by the principle of virtual work.
Mechanical Efficiency
In practical mechanical problems, friction forces are always involved. Friction
force is a non-conservative force depending on the path travelled. Friction
force can be constructive or destructive force. Friction force in a ladder
problem is a constructive force, but friction force in the clamping vise problem
can be a destructive force. Since work is used to overcome the work due to
the friction force, the work output of a mechanical device is usually less
than the work input to the mechanical device. The mechanical efficiency, η of
a mechanical device is defined as the ratio of the output work over the input
work to measue the efficiency of a mechanical design for a device or machine.
Imply 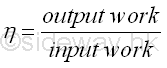
For example a toggle vise,
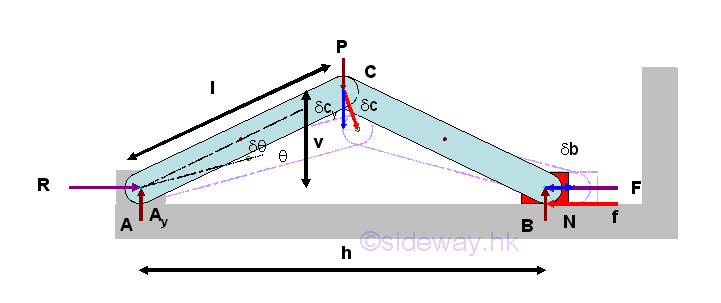
The relation between two virtual displacements along the two interested forces can be determined using differential calculus. Geometrically, the positions of points C and B can be expressed in term of the length, l of linkage and the leaning angle, θ. Therefore the virtual differential displacements can be obtained by differentiation. And the relation between two virtual displacements can then be obtained by equating the two relations. Imply
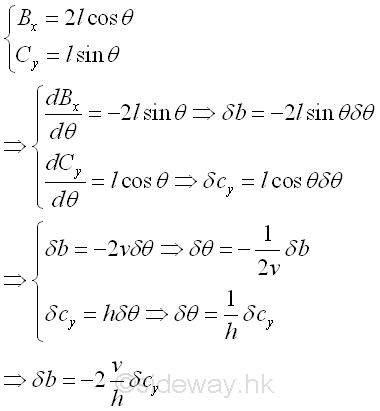
Consider an ideal case, with friction force, f equal to zero. Since a virtual counter-clockwise angular displacement along with the angular dimension, θ is in positive sense, the virtual clockwise angular displacement implies a negative sense of the virtual displacements. Therefore the sense of virtual displacements are determined by the virtual angular displacement. Besides, the two virtual displacement are in opposite sense. Applying the principle of virtual work. Imply
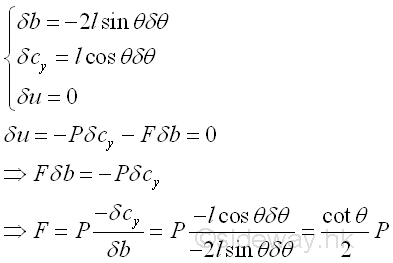
The mechanical efficiency of the ideal case is equal to one. Imply

Consider a practical case, with friction force, f equal to f. Since a virtual counter-clockwise angular displacement along with the angular dimension, θ is in positive sense, the virtual clockwise angular displacement implies a negative sense of the virtual displacements. Therefore the sense of virtual displacements are determined by the virtual angular displacement. Besides, the two virtual displacement are in opposite sense. Similarly, applying the principle of virtual work. Imply
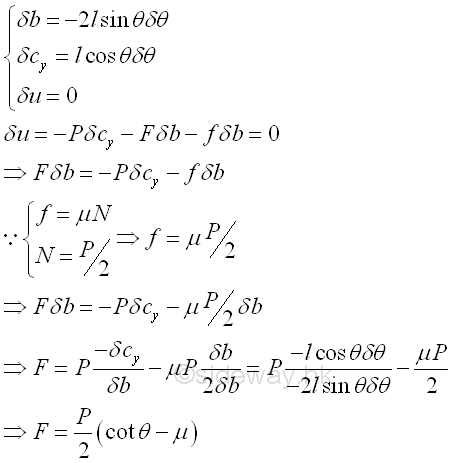
The mechanical efficiency of the practical case is

When there is no friction al force, μ is equal to zero, the mechanical efficiency, η is equal to 1. And the mechanical efficiency is equal to zero when μtanθ is equal to 1. Therefore the coefficient of friction should be limited to a value such that μtanθ i is smaller than 1. Imply
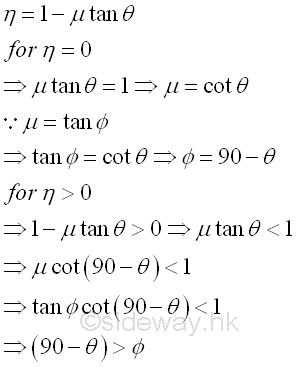
©sideway
ID: 121100089 Last Updated: 12/10/2012 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/10/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 26![]()
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
