Content
Acoustic 3D Plane Wave
Continuity Equation, 3D
Euler's Equation of Inviscid Motion, 3D
Acoustic 3D Plane Wave
The 1D plane wave can be extended into a 3D plane wave by considering a rectangular volume with coordinates x, y, z.
Continuity Equation, 3D
For a control volume, from the principle of conservation of mass, the instantaneous rate of change of mass in a control volume equals to the net mass flux flow into or out of the control volume, therefore:

As in 1D plane wave, the linearized form is :
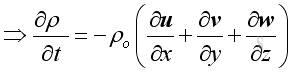
And the time derivative of the equation is:
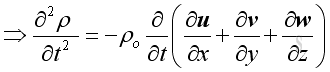
Euler's Equation of Inviscid Motion, 3D
For a control volume, from principle of momentum conservation, the instantaneous rate of change of net momentum of a control volume equals to the net applied force and the net momentum change due to the momentum flux flow into or out of the control volume. The applied force in this case is pressure only and no other forces, no gravity, no viscous force etc., then:
In x direction:

As in 1D plane wave, the linearized form is :
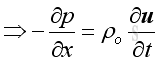
And the position derivative of the equation is
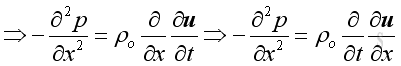
Similarly in y and z direction is
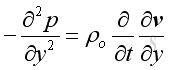 and
and 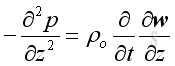
And get::
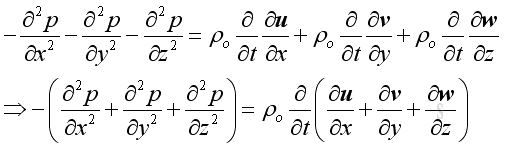
Equate two equations::
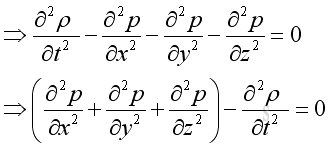
Wave Equation, 3D
Applying the equation of state and substitute the speed of propagation, imply.
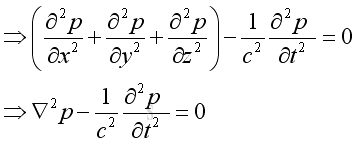
Plane Wave in 3D
Assume harmonic sound wave, imply
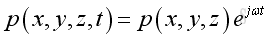
substitute the harmonic function into the 3D wave equation and take the time differential operation, imply:
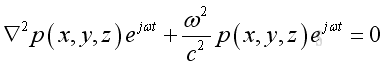
and get the Helmholtz equation:
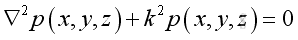
Assume the pressure is of format:
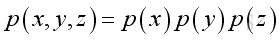
substitute the pressure function into the Helmholtz equation, and take the Laplacian differential operation:
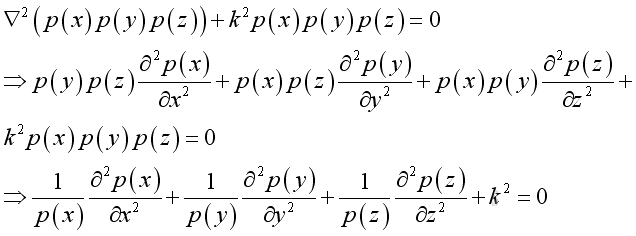
let the dispersion equation :
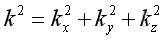
substitute into the Helmholtz equation:
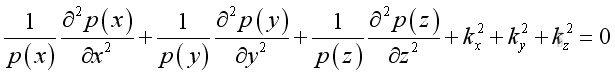
By separating the variable, imply:
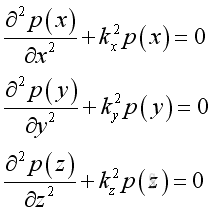
The corresponding solutions are:
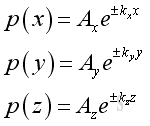
substute all into the pressure function and get the solution of wave equation is:
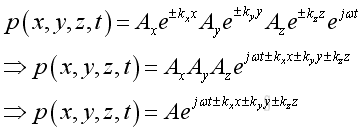
Therefore a propagating wave can be decomposed into three components along three axes. A positive sign implies a forward wave from the source to the free space. While a negative sign implies a reflected wave. With the dispersion of the value, k into three components along the three axes
©sideway
ID: 101000014 Last Updated: 10/16/2010 Revision: 0 Ref:
References
- Michael P. Norton; Denis G. Karczub,, 2003, Fundamentals of Noise and Vibration Analysis for Engieer
- G. Porges, 1977, Applied Acoustics
- Douglas D. Reynolds, 1981, Engineering Principles of Acoustics:; Noise and Vibration Control
- Conrad J. Hemond, 1983, Engineering Acoustics & Noise Control
- F. Fahy, 2001, Foundations of Engineering Acoustics
- D.A. Biew; C.H. Hansen, 1996, Engineering Noise Control: Theory and Practice
Latest Updated Links
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 25![]()
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
