Content
Acoustic Spherical Wave
Acoustic Spherical Wave Equation
Acoustic Spherical Wave
Acoustic Spherical Wave
When a small spherical sound source propagates outward uniformly and radically in a free space. The acoustic functions are spherically symmetric and therefore are functions of time and radial coordinate only.
Acoustic Spherical Wave Equation
Since there is no tangential motion during wave propagation, the spatial operator on the pressure in the wave equation can be converted to
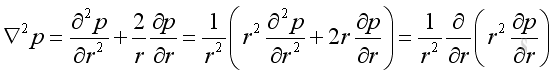
substitute the spherical operator into the rectangular wave equation:
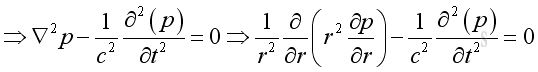
Therefore the 3D wave equation in spherical coordinate system is:
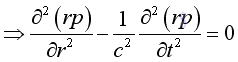
Acoustic Spherical Wave
The general solution of the spherical wave is:
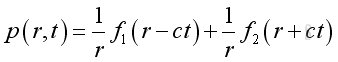
for harmonic wave, it can be expressed as
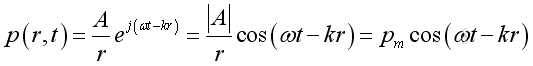
or
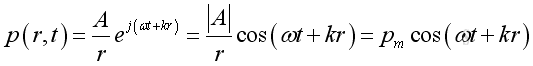
The acoustic pressure of a spherical wave is inversely proportional to the distance from the source. Therefore when the distance r is doubled, the pressure will be reduced by 6dB.
Since there is no tangential motion in spherically symmetric wave, a linearized relationship with spherical coordinates between radial velocity and radial pressure from the momentum conservation can be obtained:
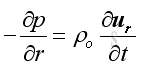
Assume the radial velocity of the form
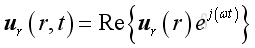
The time derivative of the velocity is:
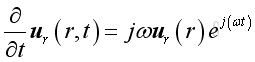
Substitute all variables into the momentum conservation equation and get the radial velocity in term of its acoustic pressure :
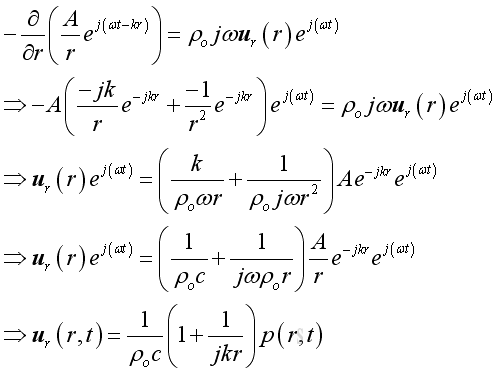
Substitute acoustic pressure into the acoustic velocity imply the real part of acoustic velocity :
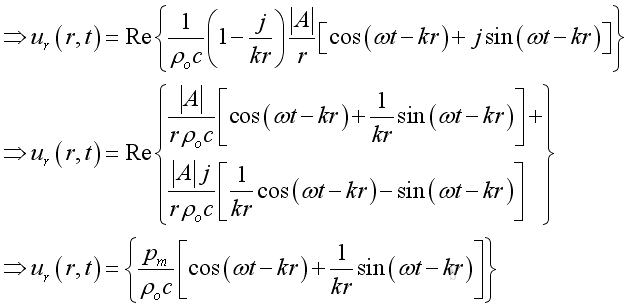
Therefore the modulus or absolute value is:
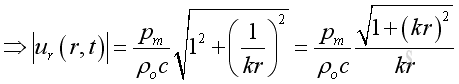
The acoustic velocity composes of two parts. The first part is in phase with the acoustic pressure with property 1/r as the propagating part. While the second part is not in phase with the acoustic pressure with property 1/r2 as the evanescent part. When the in phase component is comparable to the not in phase component, the position of interest is in the near field. Otherwise it is in the far field.
The root mean square velocity is:
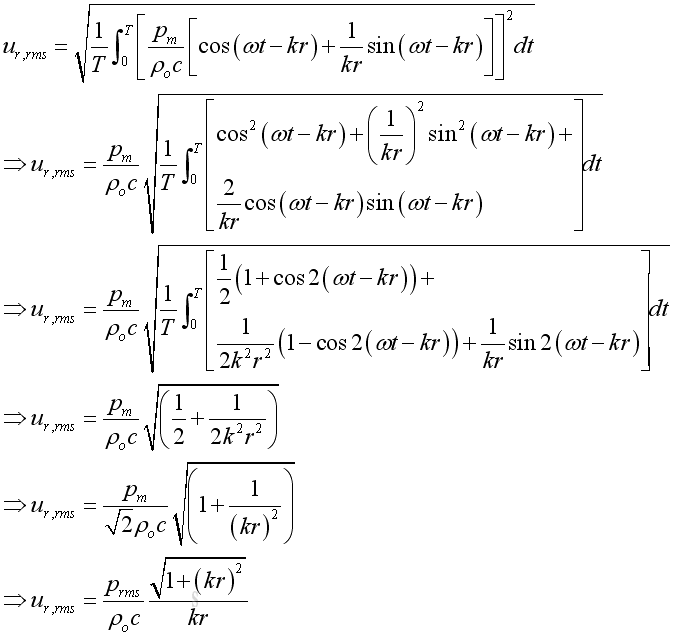
Acoustic Intensity
Similar to the plane wave, the instantaneous intensity is:
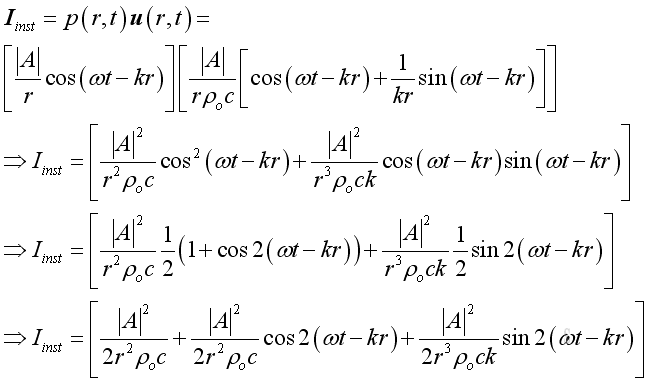
Similarly, the intensity usually expressed as an average in practice. The mean or time average intensity, in which the cosine and sine term of function of time becomes zero, imply:
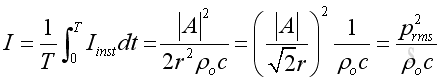
Although the expression for a spherical wave is same as that for the plane wave, the root mean square acoustic pressure is no longer a constant and is inversely proportion to the distance r from the source.
Besides, only the propagating component contributes the intensity. The evanescent component is not in phase with the pressure becomes zero after the time average process because of its oscillating property
Acoustic Power
The total acoustic power is the integration of intensity over the spherical area enclosing the enclosure and equals
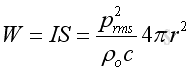
The total acoustic power is a constant and independent of distance r. Since the acoustic pressure is inversely proportion to r and the spherical surface area is proportion to r2. As intensity is proportion to square acoustic pressure, the distance r will be cancelled.
©sideway
ID: 101000015 Last Updated: 10/16/2010 Revision: 0 Ref:
References
- Michael P. Norton; Denis G. Karczub,, 2003, Fundamentals of Noise and Vibration Analysis for Engieer
- G. Porges, 1977, Applied Acoustics
- Douglas D. Reynolds, 1981, Engineering Principles of Acoustics:; Noise and Vibration Control
- Conrad J. Hemond, 1983, Engineering Acoustics & Noise Control
- F. Fahy, 2001, Foundations of Engineering Acoustics
- D.A. Biew; C.H. Hansen, 1996, Engineering Noise Control: Theory and Practice
Latest Updated Links
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight(last updated On 12/6/2025)
- Travel Singapore Rail Network(last updated On 12/5/2025)
- Travel Singapore Things to Know(last updated On 12/4/2025)
- Travel Singapore(last updated On 12/3/2025)
- Legrand Galion(last updated On 12/2/2025)
- Schneider Electric AvatarOn(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 25![]()
Reference 79
Hardware 54
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
