Moment of force in 3D about a point
When an application is subjected to forces in space, the determination of the effective moment of forces about a reference point is much more complicated than application with forces in a plane. In most case, the effective moment in space can only be determined by moment vectors addition in space instead of algebraic addition of moment vectors in the 2D case.
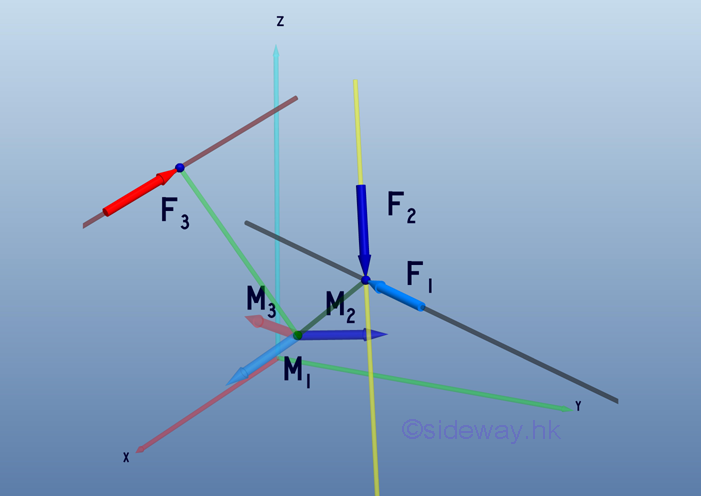
Moment Decomposition
Since the effective moment of concurrent forces about a reference point is equal to the sum of the moments of the concurrent forces as stated in Varignon's Theorem. Both the force vector and the position vector can be resolved into three rectangular components as in the 2D case.
A force vector, F in space can be resolved into three retangular components, Fx Fy and Fz. The position vector, r in space can also resolved into three retangular components, dx, dy and dz. Similarly, the moment vector, M of force, F can also be resolved into three retangular components, Mx, My and Mz.
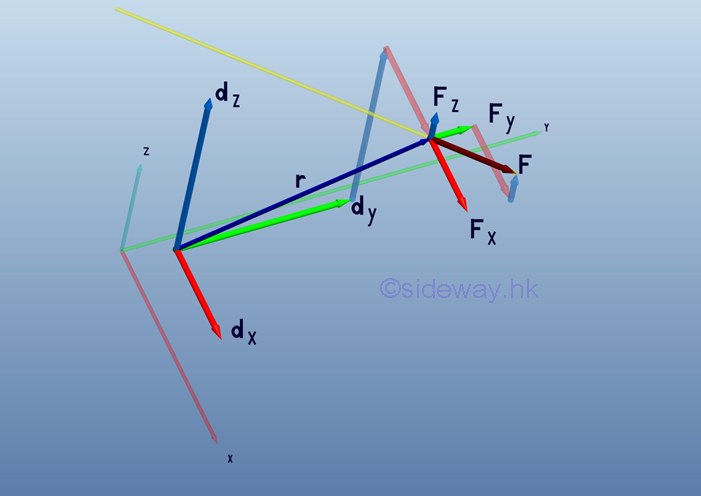
Therefore, the force vector, F and position vector, r can be expressed as:
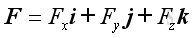 and
and
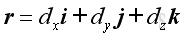
And express the resultant moment vector, M in the form of three retangular components
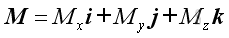
The moment M of a force F about a reference point can be defined as the vector product of r and F.
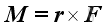
Imply.
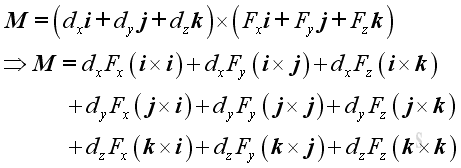
Since the magnitude of vector product is the product of the magnitudes of the two vectors and the sine of the angle formed by the vectors, imply
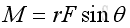
Therefore, the vector product of a unit vector with itselt is equal to a zero vector, imply
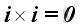 ,
,
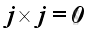 and
and
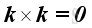
For the sense of the direction, the vector product of two different unit vectors is equal to the unit vector in the third dimension according to the right hand rule, imply
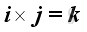 ,
,
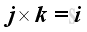 and
and
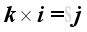
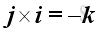 ,
,
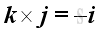 and
and
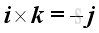
Substitute all variables into the moment vector equation, imply
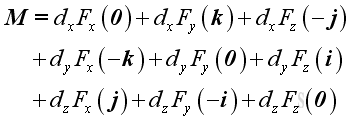 .
.
Each force component exerts zero moment along its own dimension, and exerts two moments with opposite sense along the other two dimensions. By grouping moments along the same dimension, moment, M can therefore be decomposed into three retangular components:
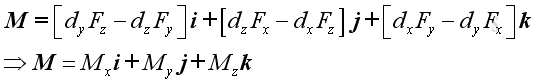 .
.
The magnitude of the three retangular components can be determined by:
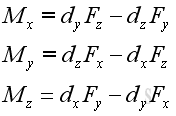 .
.
The sense or direction of the moment is indicated by the sign of the retangular resultant component.
The moment can be expressed in the determinant form:
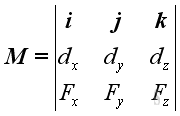 .
.
Moment Addition
The effective moment of forces about a reference point in space can be represented by a moment vector, M, in three dimensional space.
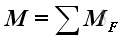 .
.
The most practical way of determining the resultant moment in space is to add up their rectangular components respectively.
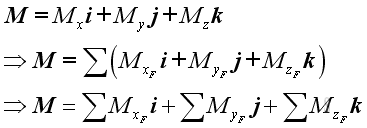 .
.
where:
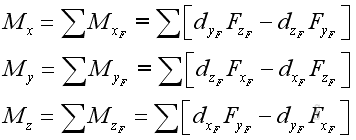 .
.
©sideway
ID: 110600002 Last Updated: 6/13/2011 Revision: 0 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Schneider Electric(last updated On 12/1/2025)
- Alfalux(last updated On 11/30/2025)
- Novabell(last updated On 11/29/2025)
- TownGas NJW12RM1(last updated On 11/28/2025)
- SamSung 42" OLED TV S90F 4K(last updated On 11/27/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/26/2025)
- Tefal BL83SD PerfectMix Cook Blender(last updated On 11/25/2025)
- Tefal KI7208 GLASS VISION KETTLE(last updated On 11/24/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/23/2025)
- Hitachi RD-290GX Dehumidifier(last updated On 11/22/2025)
- Panasonic EH-5282 Hair Dryer(last updated On 11/21/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 53
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
