Content
System of Forces Reduction
Vector Decomposition
Equivalent Systems of Forces
Types of Equivalent Systems of Forces
System of Forces Reduction
When a force system consists of more than one force, the system of forces should be reduced to one force and one couple. System of forces, F1, F2, and F3 acting on a rigid body at points, A, B, and C, respectively can be transformed to the point of interest, O through force vector transformation,
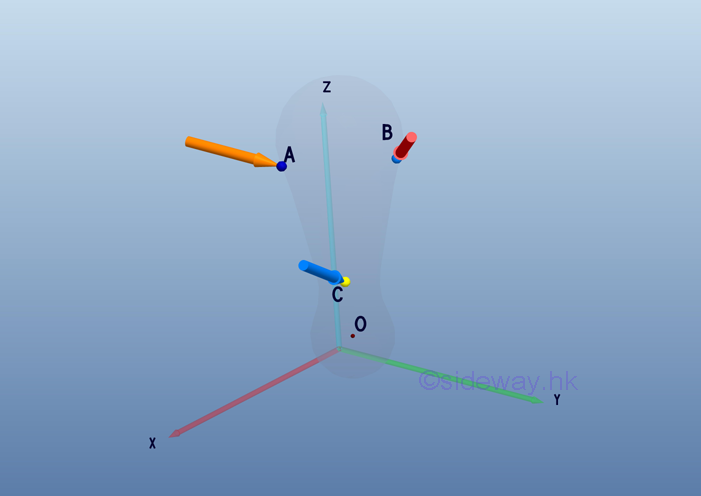
According to force vector transformation, forces at different points of application can be moved to the point of interest, O. And the moments of forces about the point of interest, O can also be determined by the cross product of the moment arm of each force vector and the force vector.
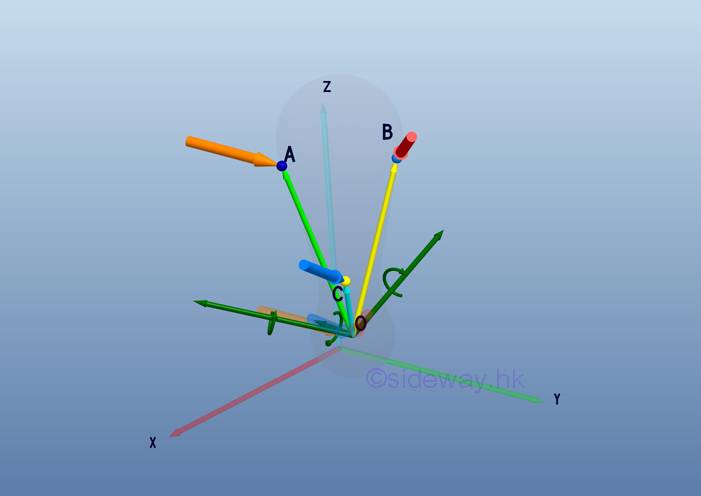
After all force vectors are moved to point O and all moment vectors are replaced by couple vectors. The equivalent system acting at a point O on a rigid body can be determined by the vector sum of the all force vectors and the vector sum of all couple vectors at the point O.
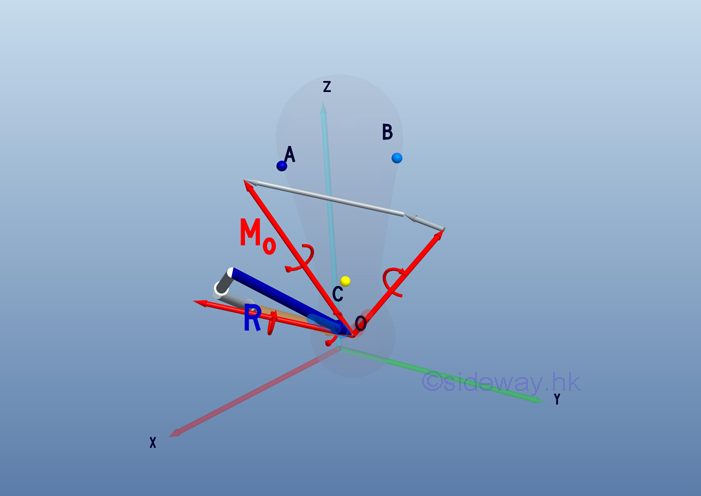
Therefore, a system of force can be reduced to an equivalent force-couple system consists of a force vector R and a couple vector MO.
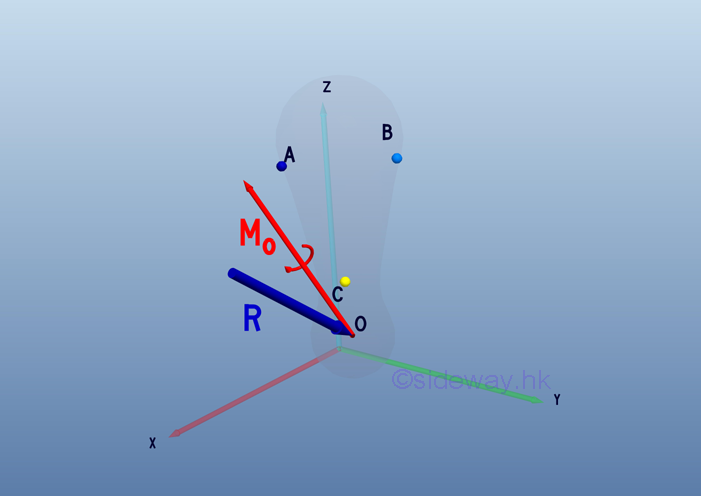
Mathematically, the force vector R and the couple vector MO of equivalent system consists can be expressed as:
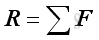 and
and
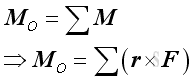
The equivalent force-couple system can then be further transferred to other points of interest through the force-couple system transformation.
Vector Decomposition
The resultant force vector and resultant couple vector can be determined in terms of rectangular compontents through vector decomposition. Imply the force vector and moment arm vector equal to:
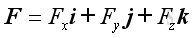 and
and
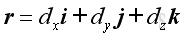
And the resultant force vector and couple vector equal to:
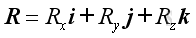 and
and
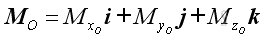
The resultant force vector equal to:
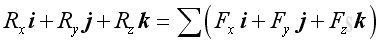
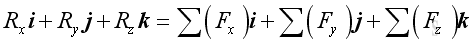
Imply:
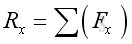
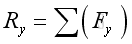
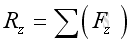
The resultant couple vector equal to:
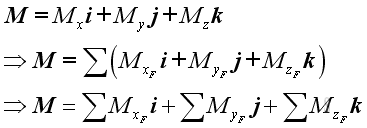 .
.
where:
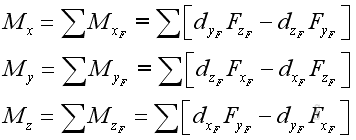
Equivalent Systems of Forces
Therefore two systems of forces are equivalent at the point of interest, if:
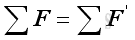 and
and
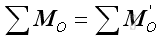
Or in terms of rectangular components:
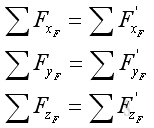 and
and
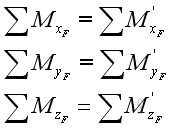
Types of Equivalent Systems of Forces
The two elements of an equivalent force-couple system at O are a resultant force vector R and a resultant couple vector MO at O.
-
When the resultant force vector R equals to zero, the force-couple system becomes a couple vector system.
-
If the force vector is not equal to zero and the couple vector is normal to the force vector, it can be reduced to a single force system through system of forces transformation.
According to the types of systems of forces, only some typical types of forces system can be reduced to an equivalent force system. They are
- All concurrent forces systems can always be reduced to a single resultant force vector.
- All coplanar forces systems can always be reduced to a single resultant force vector lying in the same plane and a couple vector prependicular to that plane. Because the force vector and couple vector are mutually perpendicular, they can be reduced to a single resultant force by moving the force vector in the plane to creat the moment about the point of interest equal to the couple vector as in Force-Couple system Reduction.
- All parallel forces systems can always be reduced to a single resultant force vector parallel to the forces of the system and a couple vector that lying in the plane normal to the force vector. Because the force vector and couple vector are mutually perpendicular, they can be reduced to a single resultant force by moving the force vector in the plane to creat the moment about the point of interest equal to the couple vector as in Force-Couple system Reduction.
-
However, if the force vector and couple vector are not matually perpendicular, it remains a force-couple system.
But when both the force vector and couple vector are equal to zero, the equivalent system of forces on the rigid body is zero.
©sideway
ID: 110700014 Last Updated: 8/2/2011 Revision: 1 Ref:
References
- I.C. Jong; B.G. rogers, 1991, Engineering Mechanics: Statics and Dynamics
- F.P. Beer; E.R. Johnston,Jr.; E.R. Eisenberg, 2004, Vector Mechanics for Engineers: Statics
Latest Updated Links
- Travel Singapore Sight Central(last updated On 1/8/2026)
- Panasonic HHGTQ1001B13 LED Floor Light(last updated On 1/7/2026)
- Travel Singapore Sight West | Central(last updated On 1/6/2026)
- Travel Singapore Sight Sentosa Sensoryscape(last updated On 1/5/2026)
- Travel Singapore Sight Sentosa Resorts World Sentosa(last updated On 1/4/2026)
- Travel Singapore Sight Sentosa HarbourFront(last updated On 1/3/2026)
- Travel Singapore Sight Sentosa(last updated On 1/2/2026)
- Travel Singapore Sight Bird Paradise(last updated On 12/30/2025)
- Travel Singapore Sight Mandai(last updated On 12/30/2025)
- Travel Singapore Sight Singapore Zoo(last updated On 12/30/2025)
- Travel Singapore Sight Rainforest Wild ASIA(last updated On 12/30/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 9
Culture
Chinese 1097
English 339
Travel 38
Reference 79
Hardware 55
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
