Content
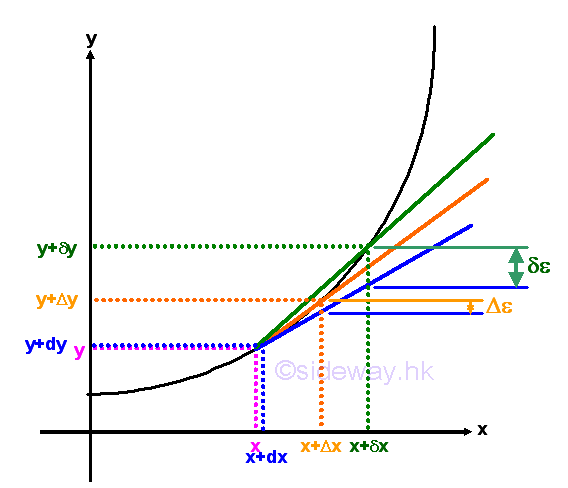
Linear Approximation Ratio
Approximation Calculation
Function Approximation Problem
Error Estimation Problem
Change Determination Problem
Linear Approximation Ratio
The previous interpretations of a derivative focuses on the position of a point by taking the limit approaching zero. In other words, the derivative of a function at a point is the most accurate approximation to the rate of change of the function at the point. Therefore the derivative of a point can be used as the linear approximation ratio or the slope of a linear function to approximate the change in a function near the point of differentiation. The accuracy of linear approximation is high when the distance away from the derivative of a point is small, i.e. δε>Δε>0
Approximation Calculation
In some practical applications, problems may be finding the change or the solutions can be approximated by a small change of the known result.
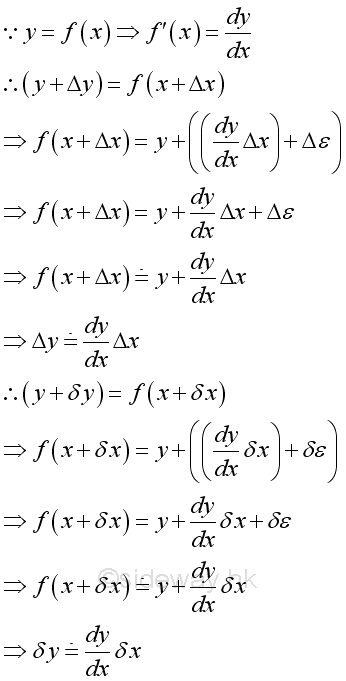
Function Approximation Problem
The value of a function of a variable can be approximated by a function of known parameter value when the difference between the variable and parameter is small.
For example, cubic root of 28. Let function y be cubic function of a variable p. A known parameter of function is 27 and the knwon solution is 3. Therefore the solution of cubic root is 3.0366 and the approximation is:
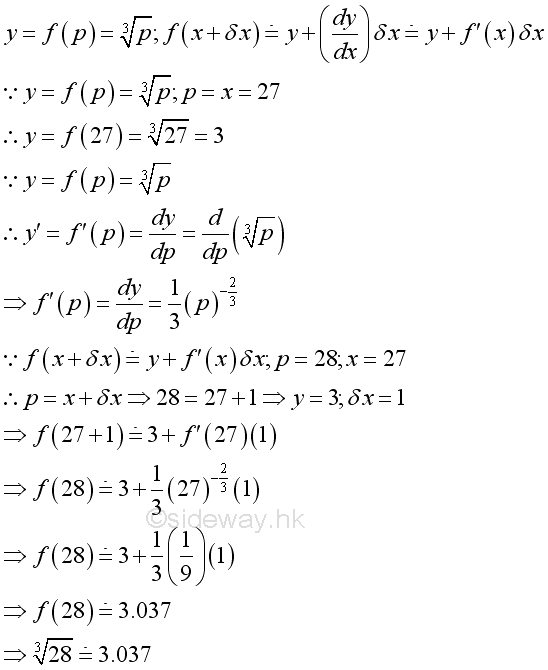
Error Estimation Problem
Measuring error is the variation in mesurements. Error is the difference between the measured value and the true value of the meausred object. The result of measuring error can be estimated by derivative.
For example, the maximum error of measuring the surfare area of a circular plate, when the measured diameter is 10 and the maximum meausring error is 0.1 is,
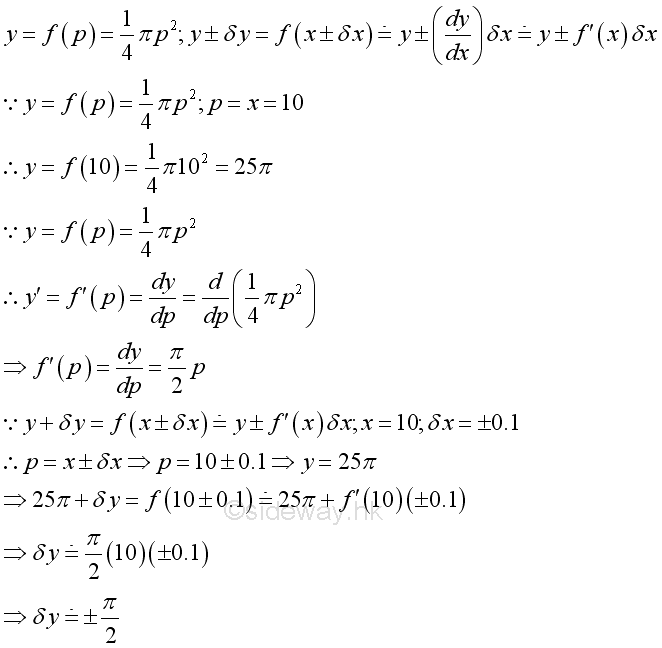
Change Determination Problem
In others word, the approximation determined by derivative can be the final change or the change. Therefore the derivative can also be used to estimate the initial value by determinating the change.
For example, square of 24.9. Let function y be square function of a variable p. A known parameter of function is 25 and the knwon solution is 625. Therefore the solution of square of 24.9 is 620.01 and the approximation is:
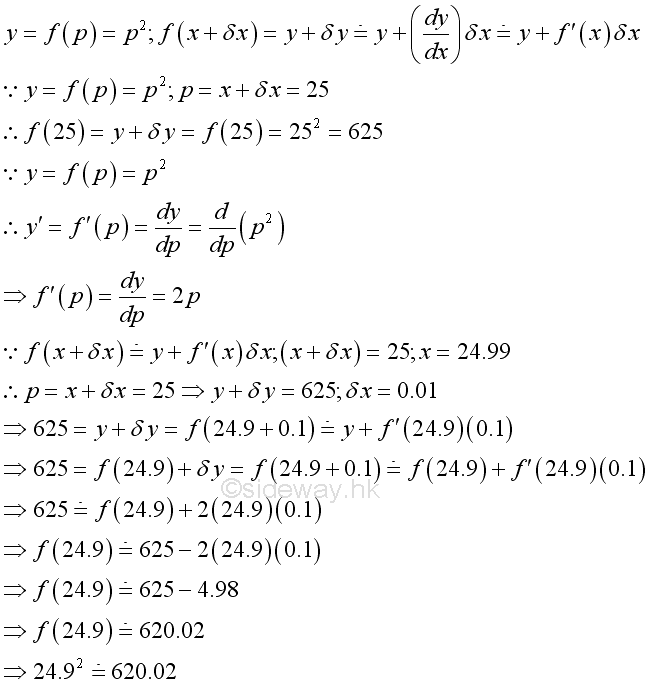
©sideway
ID: 111000013 Last Updated: 10/16/2011 Revision: 0 Ref:
References
- S. James, 1999, Calculus
- B. Joseph, 1978, University Mathematics: A Textbook for Students of Science & Engineering
Latest Updated Links
- Philips CL400 Ceiling Light 13W(last updated On 10/30/2025)
- Ikea TISKEN basket(last updated On 10/29/2025)
- Ikea TISKEN towel rack(last updated On 10/28/2025)
- Ikea REXBEGONIA mattress protector(last updated On 10/27/2025)
- Ikea KEJSAROLVON mattress protector(last updated On 10/26/2025)
- Ikea KVARNVEN ergonomic pillow(last updated On 10/25/2025)
- Ikea BRUKSVARA pocket prung mattress(last updated On 10/24/2025)
- Ikea VÅGSTRANDA pocket sprung mattress super firm(last updated On 10/23/2025)
- Ikea VITVAL underbed(last updated On 10/22/2025)
- Ikea SLÄKT bed frame with slatted bed base(last updated On 10/21/2025)
- ASUS TUF ESD-T1A External SSD Enclosure(last updated On 10/20/2025)

 Nu Html Checker
Nu Html Checker  53
53  na
na  na
na
Home 5
Business
Management
HBR 3
Information
Recreation
Hobbies 8
Culture
Chinese 1097
English 339
Travel 18
Reference 79
Hardware 23![]()
Computer
Hardware 259
Software
Application 213
Digitization 37
Latex 52
Manim 205
KB 1
Numeric 19
Programming
Web 289
Unicode 504
HTML 66
CSS 65
SVG 46
ASP.NET 270
OS 431
DeskTop 7
Python 72
Knowledge
Mathematics
Formulas 8
Set 1
Logic 1
Algebra 84
Number Theory 206
Trigonometry 31
Geometry 34
Calculus 67
Engineering
Tables 8
Mechanical
Rigid Bodies
Statics 92
Dynamics 37
Fluid 5
Control
Acoustics 19
Natural Sciences
Matter 1
Electric 27
Biology 1
